Hans Walser, [20220131]

Sierpinski-n-Eck

1 Worum geht es

Das Sierpinski-Dreieck wird auf regelmäßige Vielecke verallgemeinert.

Fleißarbeit mit vielen Bildern.

2 Beispiele

2.1 Zweieck

Das Zweieck ist eine Strecke. Ohne Rand gezeichnet, sehen wir gar nichts. Mit Rand gezeichnet, sehen wir Strecken, die sich zu einer zusammenhängenden Strecke zusammenfügen. Die individuellen Zweiecke gehen unter.

Das Problem lässt sich lösen, indem wir Kreisscheiben zeichnen (Abb. 1). Aber auch so ist das Resultat nicht umwerfend.

Der Skalierungsfaktor ist ½. Die Längen, zum Beispiel die Kreisradien, werden bei jedem Schritt halbiert.

Abb. 1: Zweieck

2.2 Dreieck

Zunächst das klassische Sierpinski-Dreieck (Abb. 2). Der Skalierungsfaktor ist ½.

Abb. 2: Sierpinski-Dreieck

Es geht auch mit Kreisen (Abb. 3).

Abb. 3: Kreise

2.3 Quadrat

Damit wir die Veränderungen sehen, müssen wir die Quadrate mit Rand zeichnen (Abb. 4). Der Skalierungsfaktor ist ½.

Abb. 4: Quadrat

Bei Kreisen kann auf die Randlinie verzichtet werden (Abb. 5).

Abb. 5: Kreise in quadratischer Anordnung

2.4 Fünfeck

Bei Fünfecken (Abb. 6) haben wir den Skalierungsfaktor von etwa 0.382. Exakt ist es der Kehrwert des Quadrates des Goldenen Schnittes.

Abb. 6: Fünfecke

Die Abbildung 7 zeigt die Situation mit Kreisen.

Abb. 7: Kreise

2.5 Sechseck

Abb. 8: Sechseck

Abb. 9: Sechseck mit Kreisen

2.6 Siebeneck

Abb. 10: Siebeneck

Abb. 11: Siebeneck mit Kreisen

2.7 Achteck

Abb. 12a: Achteck

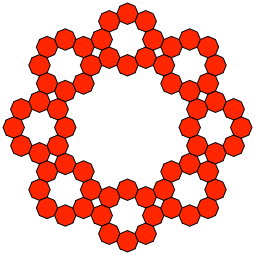
Abb. 12b: Standbild

Abb. 13: Achteck mit Kreisen

3 Technisches

3.1 Idee

Die Idee ist folgende.

In ein regelmäßiges n-Eck mit Umkreisradius 1 werden n verkleinerte (skalierte) n-Ecke je in eine Ecke verschoben. Die Skalierung soll so sein, dass benachbarte n-Ecke sich berühren. Die Berührung kann an einer Ecke oder längs einer Kante stattfinden.

Bei der Version mit Kreises sollen die Kreise gleich wie die n-Ecke positioniert sein. Benachbarte Kreise sollen sich berühren.

3.2 Benötigte Daten

Folgende von n abhängige Schlüsselzahlen sind relevant:

1. Der Skalierungsfaktor s

2. In der Kreisversion der Radius r des Startkreises.

3.3 Fallunterscheidungen

Für die Berechnung der Schlüsselzahlen sind folgende Fallunterscheidungen erforderlich:

1. Eckenzahl n ungerade.
In diesem Fall ist: s[n] = (sin(Pi/n))/(cos(Pi/2/n)+sin(Pi/n)), r[n] = sin(round(n/4)*2*Pi/n).

2. Eckenzahl n gerade

2.1 Eckenzahl n durch zwei, aber nicht durch vier teilbar.
In diesem Fall ist: s[n] = (sin(Pi/n))/(cos(Pi/n)+sin(Pi/n))), r[n] = cos(Pi/n).

2.2 Eckenzahl n durch vier teilbar.
In diesem Fall ist: s[n] = (sin(Pi/n))/(1+sin(Pi/n))), r[n] = 1.

3.4 Schlüsseldaten

Die Tabelle 1 gibt die ersten numerischen Daten. Wir sehen den Effekt der Fallunterscheidungen.

n	s[n]	r[n]
2	.5000000000	1
3	.5000000000	.8660254040
4	.5000000000	.7071067810
5	.3819660112	.9510565165
6	.3333333333	1
7	.3079785283	.9749279123
8	.2928932189	.9238795325
9	.2577728011	.9848077531
10	.2360679776	1
11	.2215655467	.9898214419
12	.2113248655	.9659258263
13	.1942458587	.9927088741
14	.1820180970	1
15	.1729090848	.9945218954
16	.1659106812	.9807852804
17	.1557880951	.9957341763
18	.1479559045	1
19	.1417478085	.9965844930
20	.1367287360	.9876883406

Tab. 1: Schlüsseldaten

Websites

Hans Walser: Schneeflocke

http://www.walser-h-m.ch/hans/Miniaturen/S/Schneeflocke/Schneeflocke.html

Hans Walser: Sierpinski, Cantor & Co.

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski/Sierpinski.htm

Hans Walser: Sierpinski-Dreieck

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski2/Sierpinski2.htm

Hans Walser: Sierpinski-Dreieck

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski3/Sierpinski3.htm

Hans Walser: Sierpinski-Fraktale

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski-Fraktale/Sierpinski-Fraktale.htm

Hans Walser: Sierpinski-Triangle

http://www.walser-h-m.ch/hans/Miniaturen/S/Sierpinski-Triangle/Sierpinksi-Triangle.mp4

Hans Walser: Sierpinski-Würfel

http://www.walser-h-m.ch/hans/Miniaturen/S/SierpinskiWuerfel/SierpinskiWuerfel.pdf