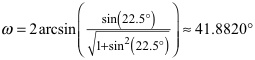Hans Walser, [20220711]

Rhombensterne

1 Worum geht es?

Sternförmige Figuren aus Rhomben. Die Sterne werden aus Rhombenspindeln zusammengesetzt.

2 Rhombenspindel

Lernen auf Vorrat. Per aspera ad astera.

2.1 Achtteiliges Beispiel

2.1.1 Aufbau der Rhombenspindel

Wir ordnen n = 8 Rhomben an gemäß Abbildung 2.1a. Die Rhomben sind kongruent. Ihre Kanten sind alle gleich steil, im gezeichneten Beispiel mit einer Steigung 1 gegenüber der Standebene, also einem Steigungswinkel 45°. Man beachte, dass der spitze Winkel der Rhomben kleiner als ein Achtel des vollen Winkels sein muss, also kleiner als 45°, damit sich die Rhomben überhaupt in den Raum erheben können. Im gezeichneten Beispiel mit der Steigung 1 gegenüber der Standebene ist der spitze Rhombenwinkel ≈ 31.3997°.

Abb. 2.1: Start und zwei weitere Schritte

In den zackenförmigen oberen Rand der Startfigur können wir einen weiteren Kranz von Rhomben einfügen (Abb. 2.1b). Diese Rhomben haben dieselbe Kantenlänge wie die Rhomben der Startfigur, die spitzen Winkel sind aber größer geworden. Analog können wir einen dritten Kranz einfügen (Abb. 2.1c). Die Abbildung 2.2 zeigt, wie es weitergeht. Aus Parallelitätsgründen haben sämtliche Rhombenkanten gegenüber der Standebene dieselbe Steigung.

Abb. 2.2a: Ansetzen von Rhombenkränzen

Abb. 2.2b: Weiteres Ansetzen von Rhombenkränzen

Die Figur schließt sich oben (nach sieben Kränzen), und wir haben eine achtteilige Rhombenspindel mit der Kantensteigung 1.

2.1.2 Variation der Kantensteigung

Die Abbildung 2.3 illustriert die Variation der Kantensteigung.

Abb. 2.3: Variation der Kantensteigung

Für den Steigungswinkel 90° der Kanten ergibt sich eine senkrechte Stange der Höhe 8. Für den Steigungswinkel 0° ergibt sich eine ebene Figur mit einem regelmäßigen Achteck als Umriss (Abb. 2.4).

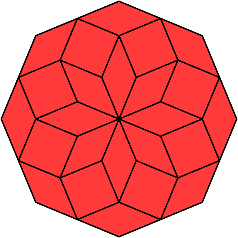
Abb. 2.4: Steigung null, Sicht von oben

Die Figur erinnert an die Fröbel-Legespiele (Abb. 2.5) (Friedrich Fröbel, 1782-1852, deutscher Pädagoge).

Abb. 2.5: Fröbel-Legespiel

2.2 24-teiliges Beispiel

Die Abbildung 2.6a zeigt die Rhombenspindel für n = 24 und die Kantensteigung 1. Sie ist eine recht gute Approximation der Kosinusspindel (Abb. 2.6b), welche einen Bogen der Kosinuskurve als Meridian hat.

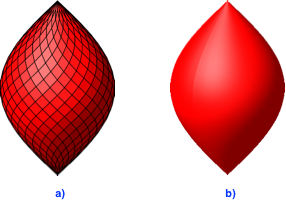
Abb. 2.6: 24-teilige Rhombenspindel. Kosinusspindel

Tatsächlich ergibt sich bei einer Kantensteigung 1 aus den Rhombenspindeln für wachsendes n die Kosinusspindel als Grenzfigur.

2.3 Anzahl Seitenrhomben

Für eine gegebene Teilung n ergeben sich (n – 1) Kränze. Wir haben also insgesamt n(n – 1) Seitenrhomben.

2.4 Regelmäßige Sonderfälle

Die Rhomben verschiedener Rhombenkränze einer Rhombenspindel sind in der Regel nicht kongruent. Die spitzen Winkel variieren. Nun gibt es aber Ausnahmen.

2.4.1 Rhombenhexaeder und Würfel

Für n = 3 erhalten wir Rhombenhexaeder mit sechs kongruenten Rhomben als Seitenflächen (Abb. 2.7).

Abb. 2.7: Rhombenhexaeder

Ein Sonderfall ist der Würfel (Abb. 2.8a). Er steht auf einer Ecke, physikalisch ein labiles Gleichgewicht.

Abb. 2.8: Würfel

Man kann mit etwas Geduld und Fingerspitzengefühl auch einen Spielwürfel auf eine (abgerundete) Ecke stellen (Abb. 2.8b). In diesem Fall haben wir sogar ein indifferentes Gleichgewicht.

2.4.2 Rhombendodekaeder

Für n = 4 erhalten wir Rhombendodekaeder (Abb. 2.9).

Abb. 2.9: Rhombendodekaeder

Die Rhomben sind nun allerdings in der Regel nicht mehr alle kongruent. Die vier Rhomben im Äquatorkranz haben andere Winkel als die Rhomben in den Polkappen. Es gibt nun aber einen Sonderfall mit zwölf kongruenten Rhomben. Um diesen Sonderfall zu finden, berechnen wir die Rhombenwinkel ω und ω‘ in Abhängigkeit des Steigungswinkels α der Kanten gemäß Abbildung 2.10.

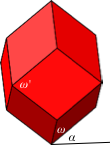
Abb. 2.10: Rhombenwinkel und Steigungswinkel der Kanten

Es ist:

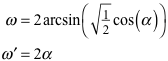
Die Abbildung 2.11 zeigt die Funktionsgrafen der beiden Winkel in Abhängigkeit des Steigungswinkels α der Kanten.

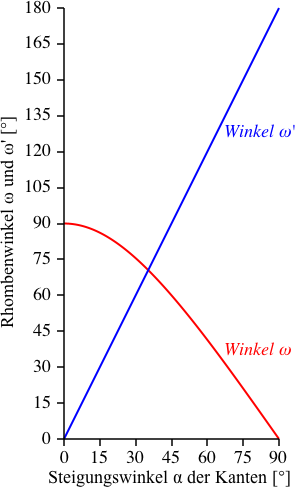
Abb. 2.11: Funktionsgrafen

Die beiden Winkel sind gleich für

und betragen dann:

Die Abbildungen 2.12 und 2.13 zeigen das zugehörige regelmäßige Rhombendodekaeder.

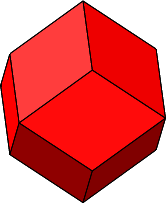
Abb. 2.12: Regelmäßiges Rhombendodekaeder

Abb. 2.13: Flechtmodell des regelmäßigen Rhombendodekaeders

Ein zweiter regelmäßiger Fall ist der Grenzfall der senkrechten Stange der Höhe 4.

2.4.3 Rhombenikosaeder

Mit einer analogen Überlegung wie beim Rhombendodekaeder finden wir für n = 5 das regelmäßige Rhombenikosaeder (Abb. 2.14 und 2.15).

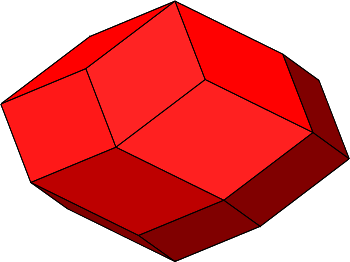
Abb. 2.14: Regelmäßige Rhombenikosaeder

Abb. 2.15: Modell des regelmäßigen Rhombenikosaeders

Beim regelmäßigen Rhombenikosaeder ergibt sich der spitze Rhombenwinkel ω = arctan(2) ≈ 63.4349°.
Ein zweiter regelmäßiger Fall ist der Grenzfall der senkrechten Stange der Höhe 6.

Man mag sich wundern, warum für n = 5 nicht das regelmäßige Rhombentriakontaeder (Abb. 2.16 und 2.17) erscheint.

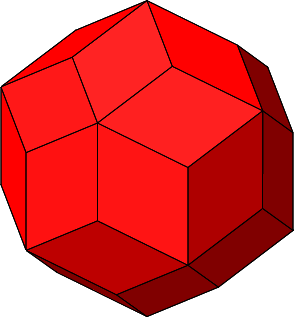
Abb. 2.16: Regelmäßiges Rhombentriakontaeder

Abb. 2.17: Flechtmodell des regelmäßigen Rhombentriakontaeders

Das regelmäßige Rhombentriakontaeder hat einen Äquatorkranz von zehn Rhomben mit senkrechten Kanten. Das passt nicht in unser System, wo alle Rhombenkanten gegenüber der Standebene denselben Steigungswinkel haben.

Es gibt aber eine Rhombenspindel mit 30 Rhomben. Dazu ist n = 6 (Abb. 2.18). Die Anzahl der Seitenrhomben ist dann n(n – 1) = 6•5 = 30.

Abb. 2.18: Rhombenspindel mit 30 Seitenrhomben

Es gibt (außer dem Grenzfall der senkrechten Stange der Höhe 6) aber keine Situation mit 30 kongruenten Seitenrhomben.

3 Nicht konvexe Beispiele

Die bisher vorgestellten Rhombenspindeln sind konvex. Wir können auch nicht konvexe Rhombenspindeln bauen. Dazu gehen wir vor wie exemplarisch folgt. Wir arbeiten mit n = 5 und ω = 70°. Die Abbildung 3.1 zeigt die Startfigur für den konvexen Fall in einer Ansicht und von oben.

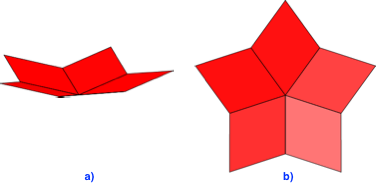
Abb. 3.1: Startfigur für den konvexen Fall

Nun ersetzen wir n = 5 durch n = 5/2 und schauen was passiert (Abb. 3.2).

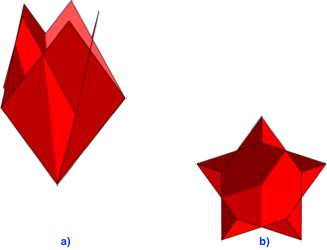
Abb. 3.2: Startfigur für den nicht konvexen Fall

Die Rhomben richten sich auf und überschneiden sich. Wir haben die Situation des Pentagramms.

Die Abbildung 3.3 zeigt, wie es weitergeht. Die Spindel ist tailliert.

Abb. 3.3: Nicht konvexe Rhombenspindel

In der Abbildung 3.4 wird die Steigung der Rhombenkanten variiert.

Abb. 3.4: Variation der Kantensteigung

Die Abbildung 3.5 zeigt den Fall 13/3.

Abb. 3.5: 13/3

Die Abbildung 3.6 zeigt das Beispiel 13/3 mit der Kantensteigung null in der Sicht von oben.

Abb. 3.6: Fensterrosette

4 Sternbeispiele

Und nun geht’s zu den Sternen.

4.1 Auf der Basis platonischer Körper

4.1.1 Tetraeder

Die Abbildungen 4.1 und 4.2 zeigen ein Tetraeder, dessen Kanten mit dem Mittelpunkt flächig verbunden sind.

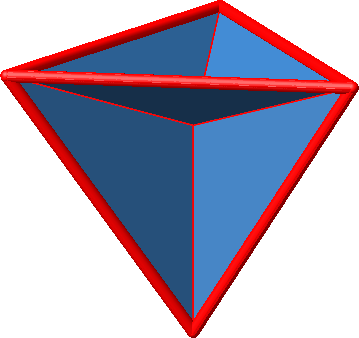
Abb. 4.1: Kantenmodell des Tetraeders

Abb. 4.2: Papiermodell für das Tetraeder

Bauanleitung für das Papiermodell hier.

Wir haben auf jeder Seite ein Dreikant-Loch. Der Winkel im Mittelpunkt ist:

Wir können also in jedes Loch eine Rhombenspindel mit n = 3 (ein Hexaeder also) und ω = arccos(–⅓) ≈ 109.4712° einpassen (Abb. 4.3).

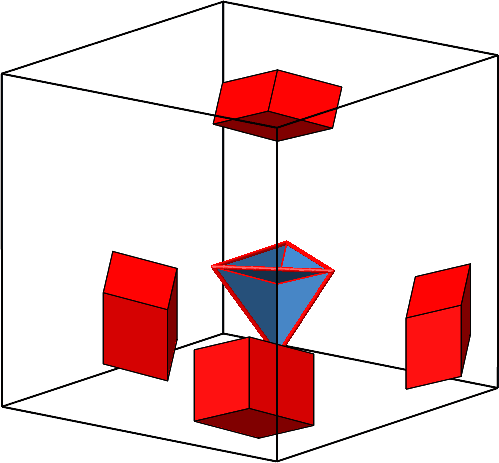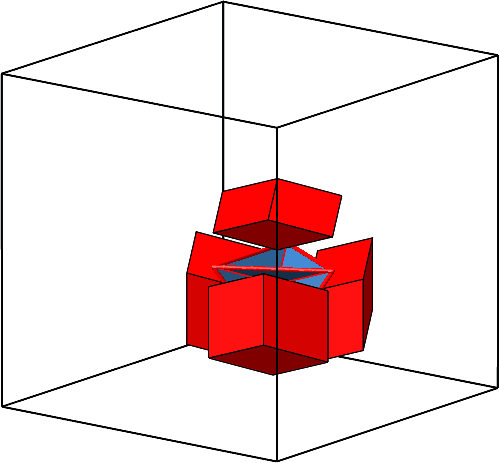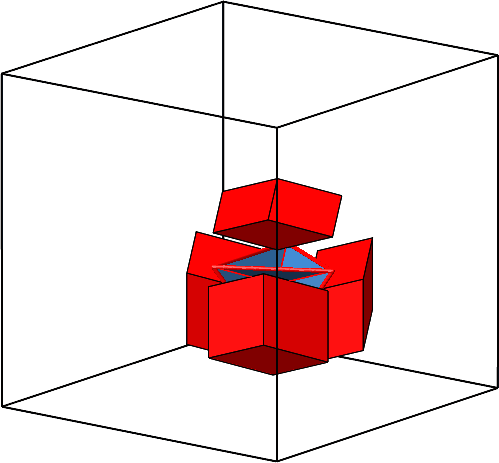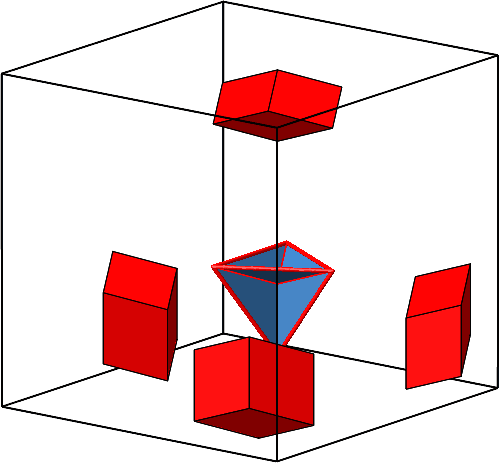
Abb. 4.3: Hexaeder einpassen

Die Abbildung 4.4 zeigt das Zusammenfügen ohne das Kantenmodell des Tetraeders.

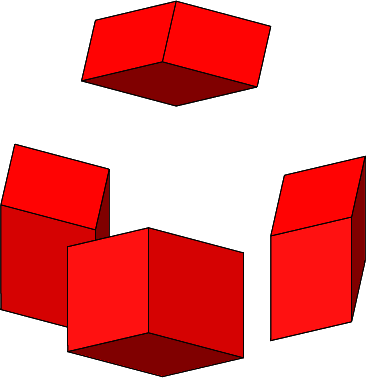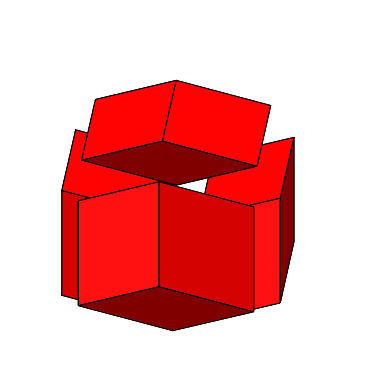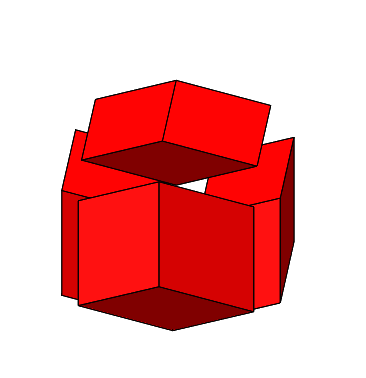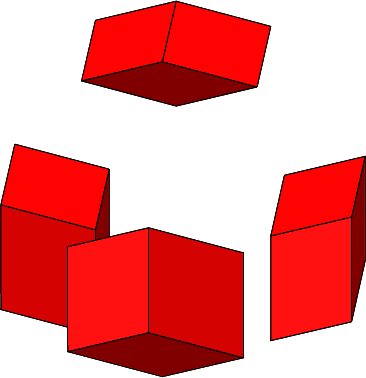
Abb. 4.4: Zusammenfügen

Die Endfigur ist ein regelmäßiges Rhombendodekaeder (Abb. 4.5, siehe auch Abb. 2.12 und 2.13). Bei dieser Figur fällt es nicht leicht, einen „Stern“ zu sehen.

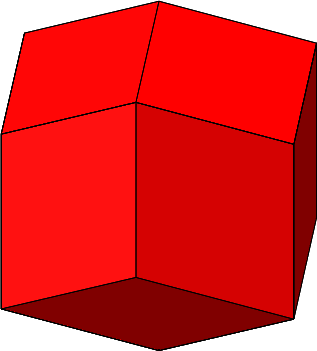
Abb. 4.5: Regelmäßiges Rhombendodekaeder

In den folgenden Beispielen zeigen wir ohne großen Kommentar das Kantenmodell, den Einpass-Vorgang und die Endfigur.

4.1.2 Oktaeder

Abb. 4.6: Kantenmodell des Oktaeders

Es ist n = 3 und ω = 90°. Die einzupassende Rhombenspindel ist ein Würfel.

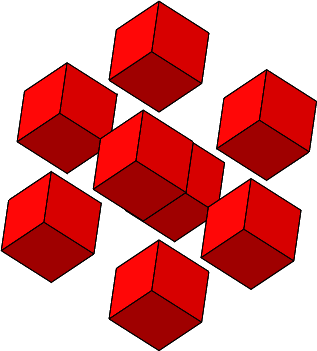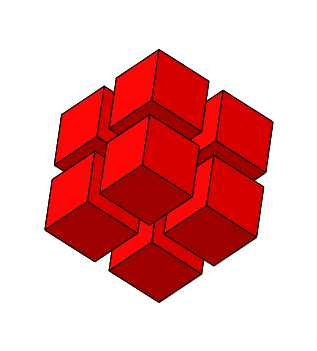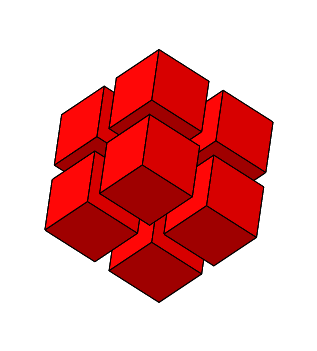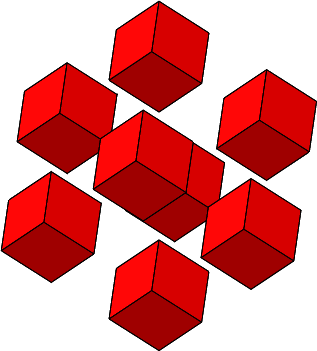
Abb. 4.7: Würfel zusammenfügen

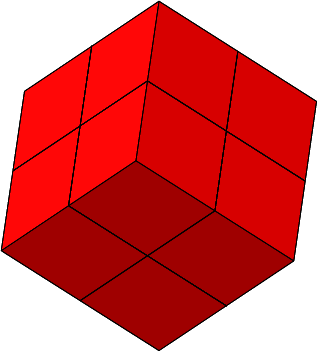
Abb. 4.8: Endfigur ein Würfel

Auch diese Endfigur kann schwerlich als Stern gesehen werden.

4.1.3 Ikosaeder

Abb. 4.9: Kantenmodell des Ikosaeders

Es ist n = 3 und ω = arctan(2) ≈ 63.4349°. Die einzupassende Rhombenspindel ist ein Rhombenhexaeder.

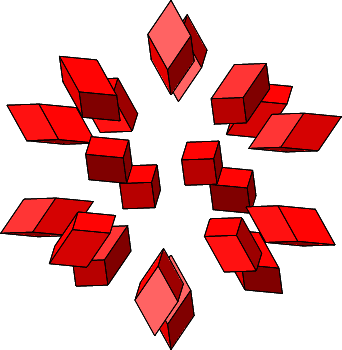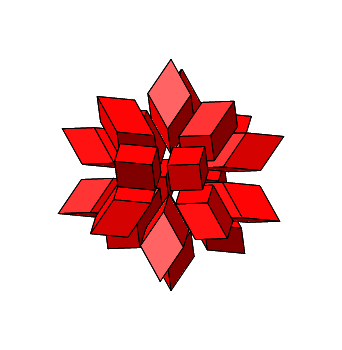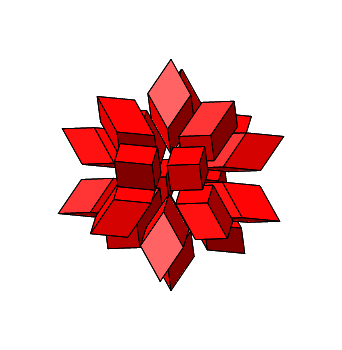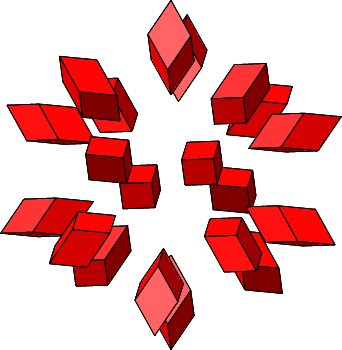
Abb. 4.10: Zusammensetzen von 20 Rhombenhexaedern

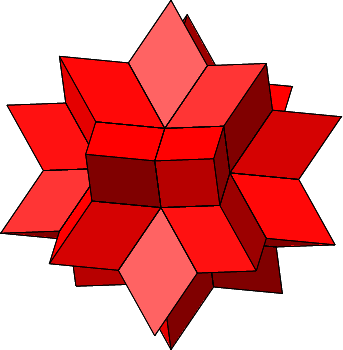
Abb. 4.11: Stern

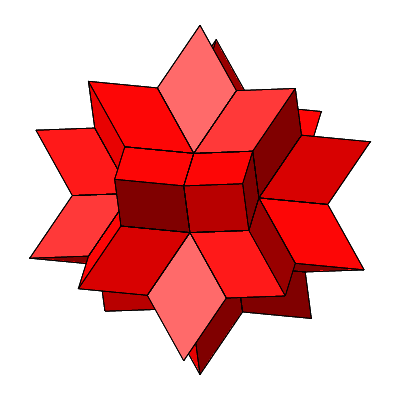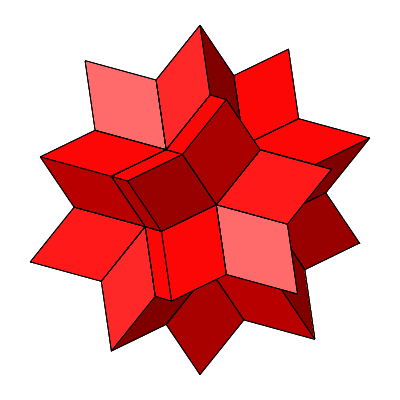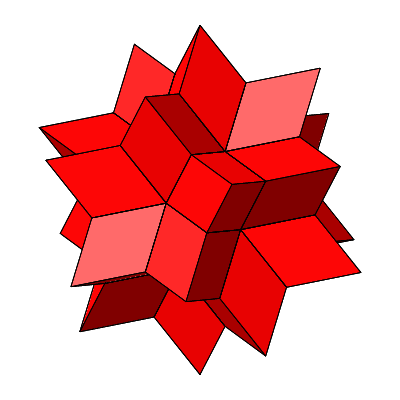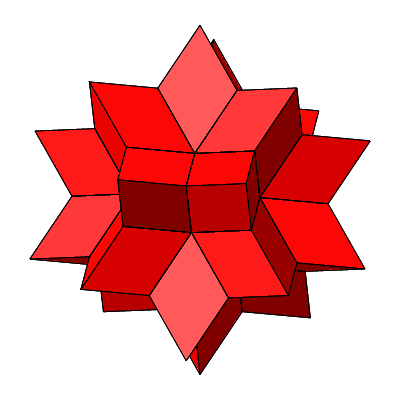
Abb. 4.12: Rotation

Abb. 4.13: Flechtmodell des Sterns

Tetraeder, Oktaeder und Ikosaeder haben gleichseitige Dreiecke als Seitenflächen. Wir haben also n = 3. Das heißt, dass wir Rhombenhexaeder einfügen können. In den folgenden Beispielen (Würfel und regelmäßiges Dodekaeder) können wir nun größere Rhombenspindeln einfügen.

4.1.4 Würfel

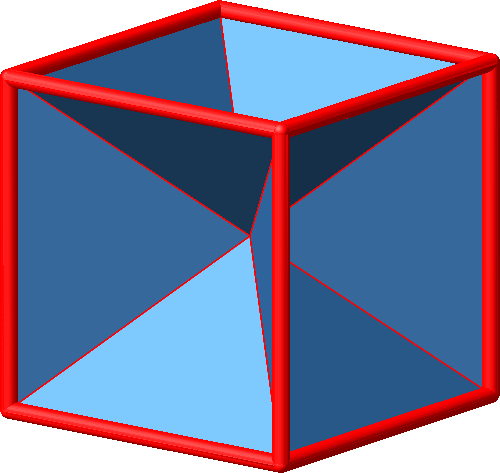
Abb. 4.14: Kantenmodell des Würfels

Abb. 4.15: Papiermodell für den Würfel

Bauanleitung für das Papiermodell hier.

Es ist nun n = 4 und ω = arccos(⅓) ≈ 70.5288°. Die einzupassenden Rhombenspindeln sind regelmäßige Rhombendodekaeder (Abb. 4.16, siehe auch Abb. 2.12 und 2.13).

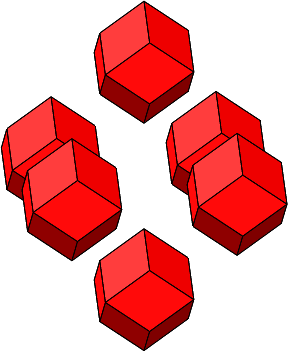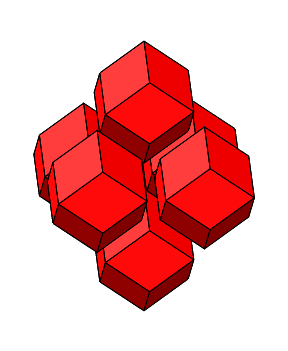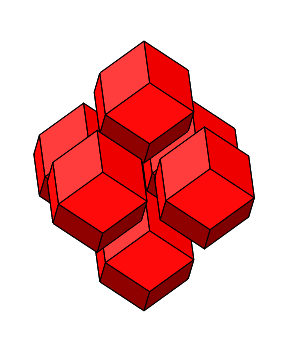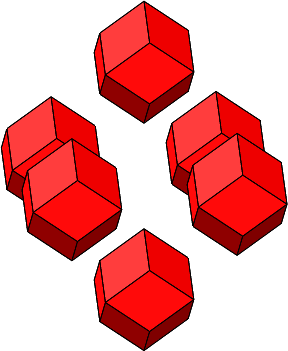
Abb. 4.16: Zusammenfügen von regelmäßigen Rhombendodekaedern

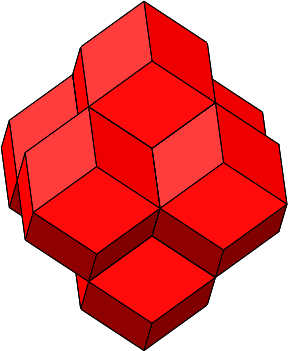
Abb. 4.17: Sechs regelmäßige Rhombendodekaeder

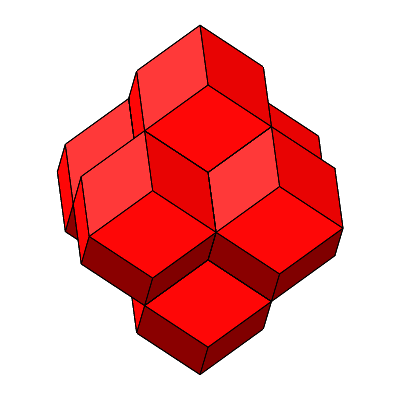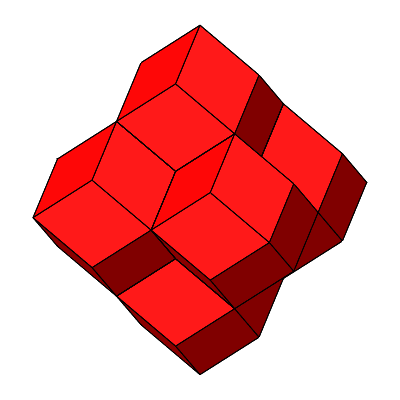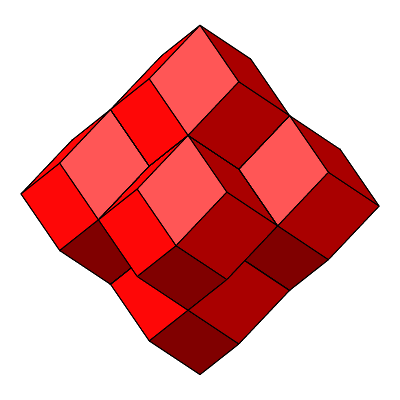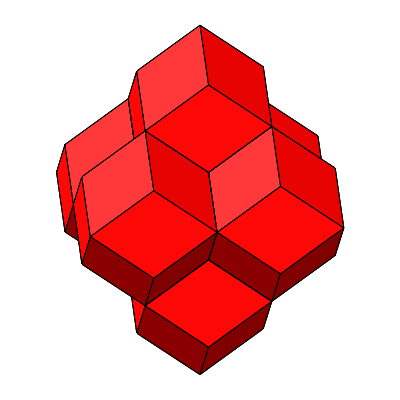
Abb. 4.18: Nun muss sich alles, alles wenden

4.1.5 Regelmäßiges Pentagondodekaeder

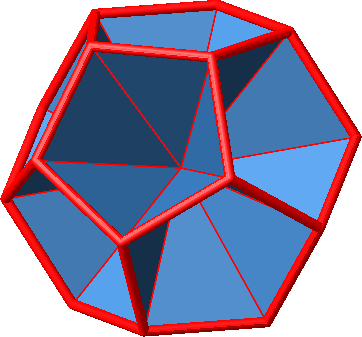
Abb. 4.19: Kantenmodell des regelmäßigen Pentgondodekaeders

Abb. 4.20: Papiermodell für das regelmäßige Pentagondodekaeder

Es ist nun n = 5 und ω = arcsin(⅔) ≈ 41.8103°.

Die Abbildung 4.21 zeigt das Zusammensetzen der zwölf Rhombenspindeln.

Abb. 4.21: Zusammensetzen der Rhombenspindeln

Abb. 4.22: Der Stern

Abb. 4.23: Rotierender Stern

Nun können wir aber noch einen draufgeben. Im Stern (Abb. 4.22 und 4.23) erkennen wir von drei kongruenten Rhomben gebildete Löcher. Die drei Rhomben haben eine Ecke mit drei spitzen Winkeln ω₂ = arccos(⅓) ≈ 70.5288° gemeinsam. Wir können also ein Rhombenhexaeder einfügen. Die Abbildungen 4.24 und 4.25 zeigen das erste derart eingefügte gelbe Rhombenhexaeder.

Abb. 4.24: Einfügen eines gelben Rhombenhexaeders

Abb. 4.25: Eingefügtes Rhombenhexaeder

Die Abbildung 4.26 zeigt sämtliche derartige gelbe Rhombenhexaeder, es sind 20 Stück. Wer’s nicht glaubt, kann nachzählen (Abb. 4.27).

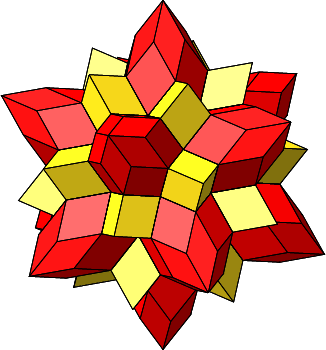
Abb. 4.26: 20 eingefügte gelbe Rhombenhexaeder

Abb. 4.27: Rotation

Die zwölf roten Rhombenspindeln haben eine Ecke im Mittelpunkt gemeinsam. Die gelben Rhombenhexaeder reichen aber nicht bis zum Mittelpunkt (Abb. 4.28).

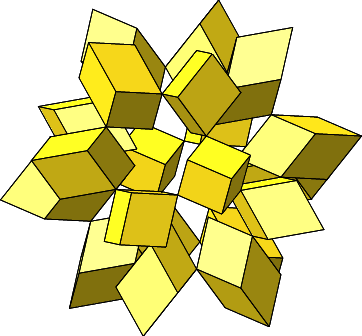
Abb. 4.28: Räumliche Anordnung der gelben Rhombenhexaeder

Jetzt können wir aber noch einen zweiten draufgeben. In der Figur der Abbildungen 4.26 und 4.27 erkennen wir von vier kongruenten Rhomben gebildete Löcher. Diese vier Rhomben sind abwechslungsweise rot und gelb, aber symmetrisch so angeordnet, dass ihre kurzen Diagonalen ein Quadrat bilden. Die vier Rhomben haben eine Ecke mit vier spitzen Winkeln ω₂ = arccos(⅓) ≈ 70.5288° gemeinsam. Wir können also eine Rhombenspindel mit n = 4 einfügen (grün in Abb. 4.29 und 4.30). Die einzufügende Rhombenspindel ist ein regelmäßiges Rhombendodekaeder (vgl. Abb. 2.12 und 2.13).

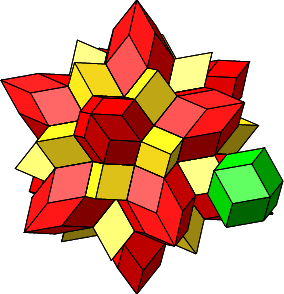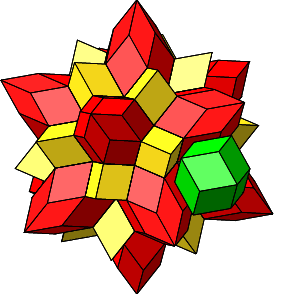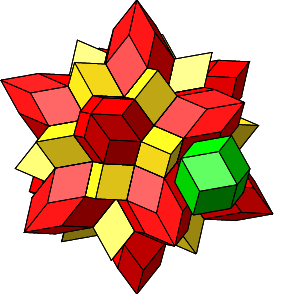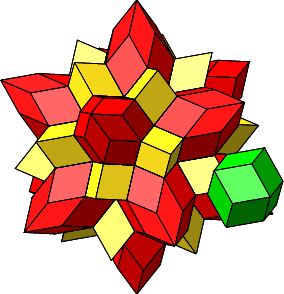
Abb. 4.29: Einfügen eines regelmäßigen Rhombendodekaeders

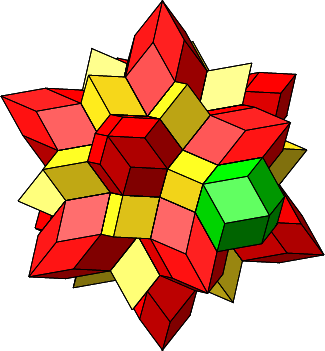
Abb. 4.30: Eingefügtes regelmäßiges Rhombendodekaeder

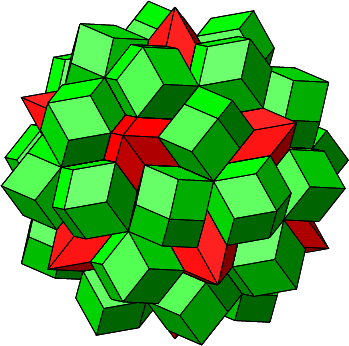
Abb. 4.31: Dreißig regelmäßige Rhombendodekaeder

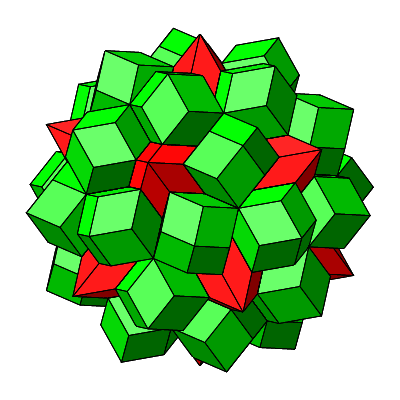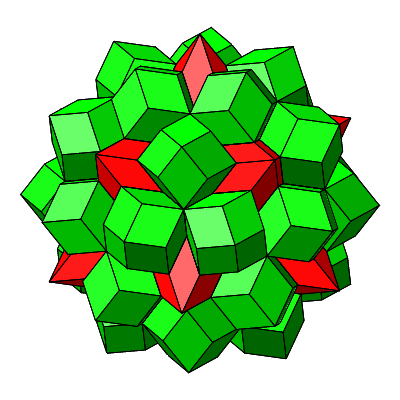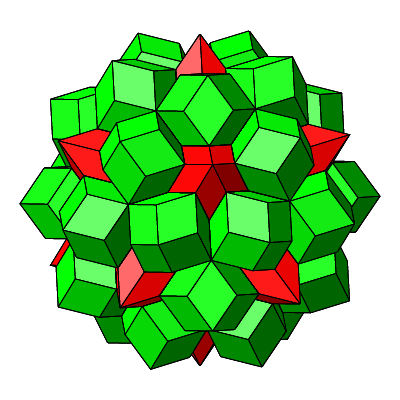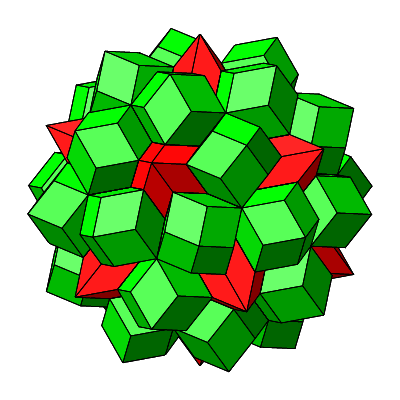
Abb. 4.32: Wie man’s auch dreht und wendet, die gelben sieht man nicht

4.2 Auf der Basis archimedische Körper

Unsere Sternkonstruktion funktioniert mit allen Polyedern, welche eine konstante Kantenlänge sowie eine Umkugel haben. Dazu gehören die platonischen Körper und die archimedischen Körper, aber auch andere Polyeder.

Im Folgenden einige Beispiele mit archimedischen Körpern als Grundlage.

4.2.1 Kuboktaeder

Abb. 4.33: Kantenmodell des Kuboktaeders

Abb. 4.34: Papiermodell

Wir haben jetzt sowohl dreieckige wie auch quadratische Löcher, wir können also mit Rhombenspindeln für n = 3 (gelb in Abb. 4.35) und für n = 4 (rot in Abb. 4.35) arbeiten. Die Winkel im Mittelpunkt sind alle ω = 60°.

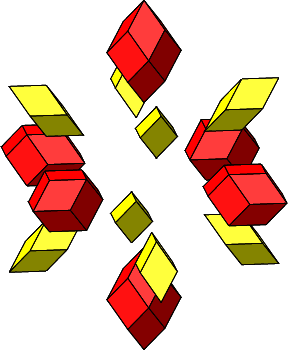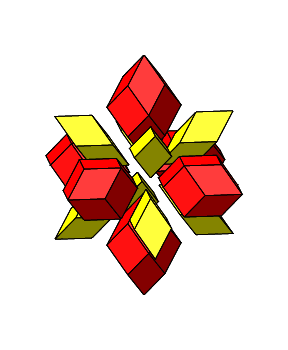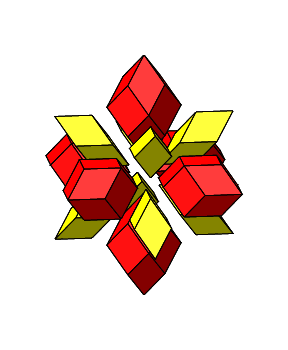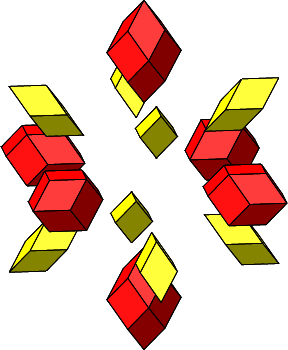
Abb. 4.35: Zusammensetzen

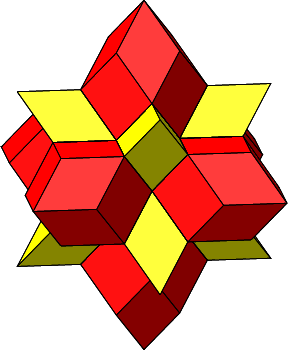
Abb. 4.36: Stern

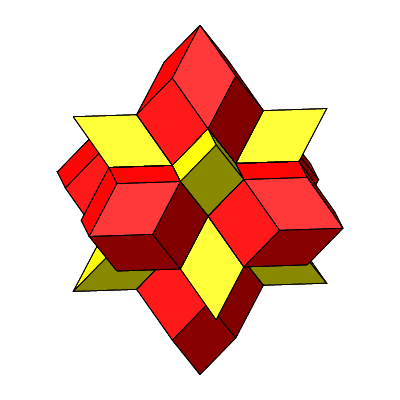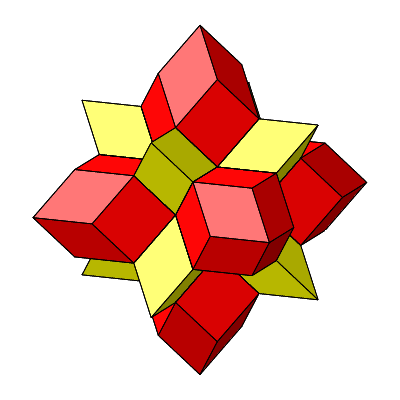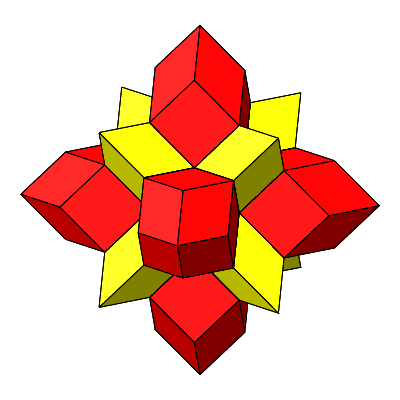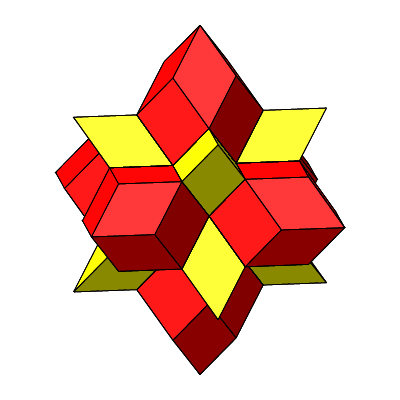
Abb. 4.37: Rotation

4.2.2 Hexaeder-Stumpf

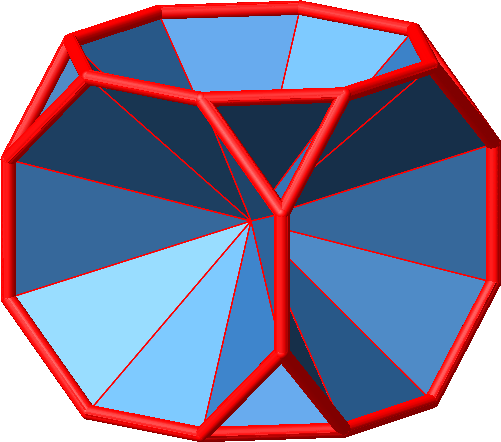
Abb. 4.38: Kantenmodell des Hexaederstumpfes

Wir können mit Rhombenspindeln für n = 3 und n = 8 arbeiten. Für den Winkel ω im Mittelpunkt erhalten wir:

Abb. 4.39: Zusammensetzen

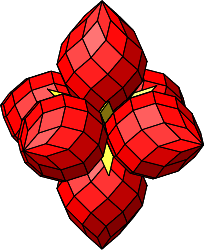
Abb. 4.40: Stern

Abb. 4.41: Rotation

Wir können Sterne der Abbildung 4.40 linear zusammensetzen (Abb. 4.41a).

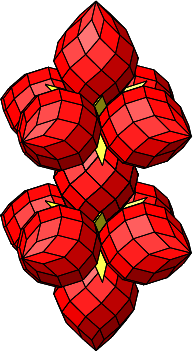
Abb. 4.42: Lineare Zusammensetzung

Es geht aber auch in drei Dimensionen (Abb. 4.43).

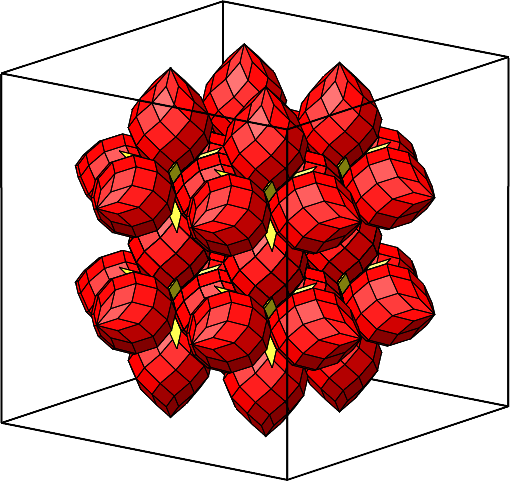
Abb. 4.43: Dreidimensionale Zusammensetzung

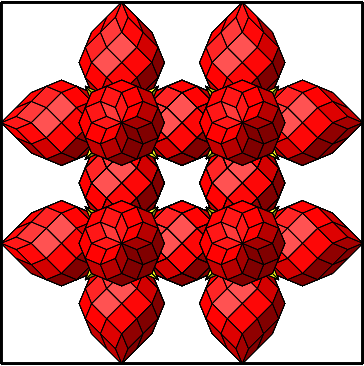
Ab. 4.44: Frontale Sicht

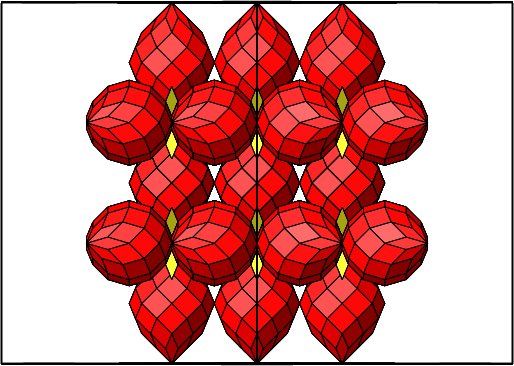
Abb. 4.45: Blick über die Kante

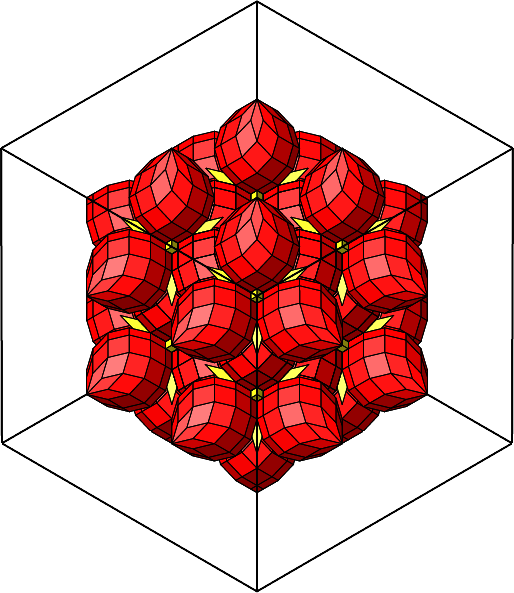
Abb. 4.46: Blick über die Ecke

4.2.3 Fußball

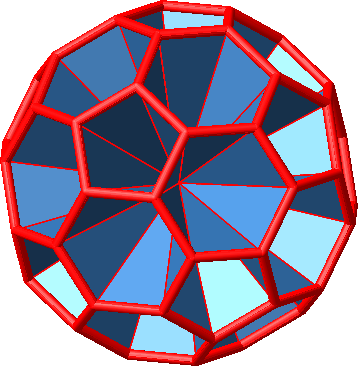
Abb. 4.47: Ikosaederstumpf (Fußball)

Es ist n = 5 und n = 6 sowie:

Abb. 4.48: Zusammenfügen

Abb. 4.49: Stern

Abb. 4.50: Rotation

4.2.4 Großes Rhombenkuboktaeder

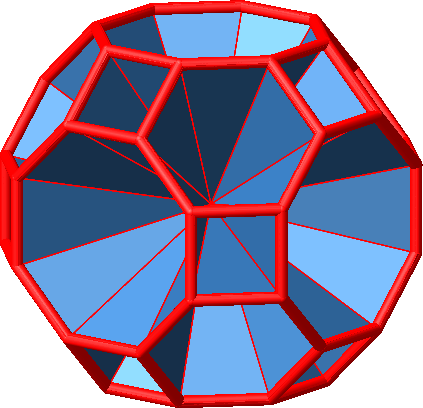
Abb. 4.51: Großes Rhombenkuboktaeder

Wir haben n = 4, n = 6 und n = 8, sowie

Abb. 4.52: Zusammenfügen

Abb. 4.53: Stern

Abb. 4.54: Rotation

4.3 Prismen

4.3.1 Siebenteiliges Prisma

Abb. 4.55: Siebenteiliges Prisma

Wir haben n = 4 und n = 7 sowie:

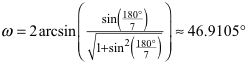
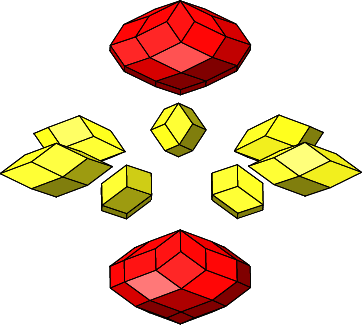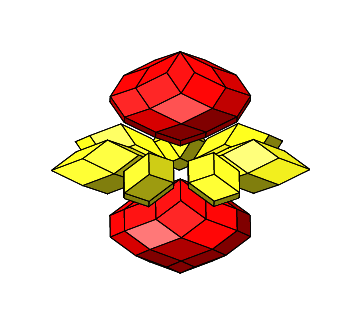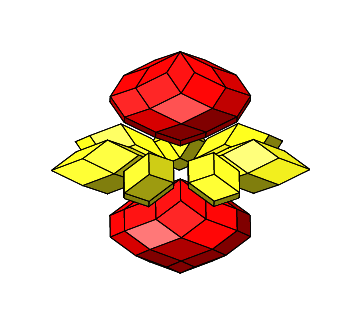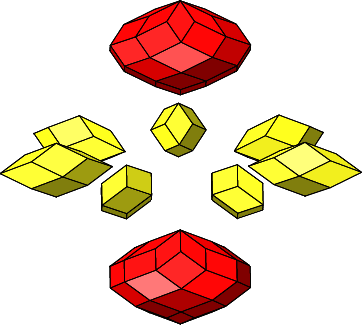
Abb. 4.56: Zusammenfügen

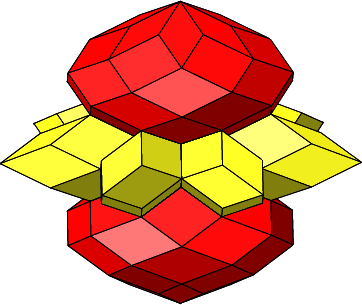
Abb. 4.57: Rhombenburger

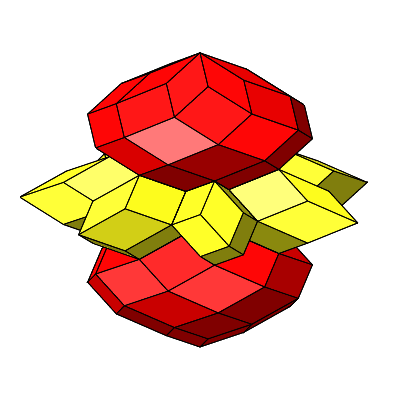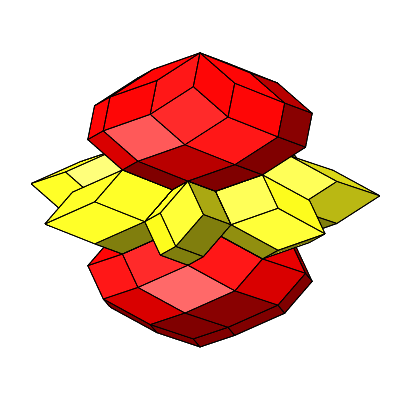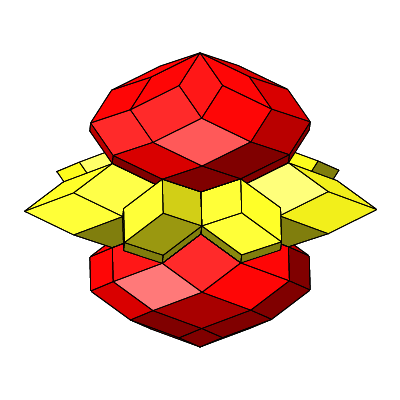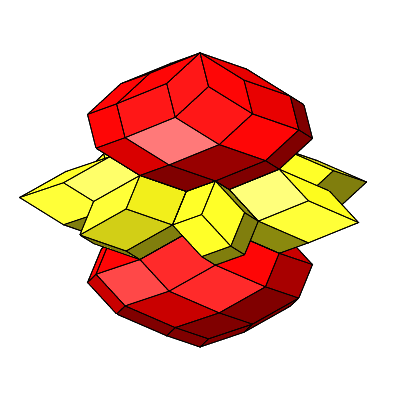
Abb. 4.58: Rotation

4.3.2 Asymmetrisches Beispiel

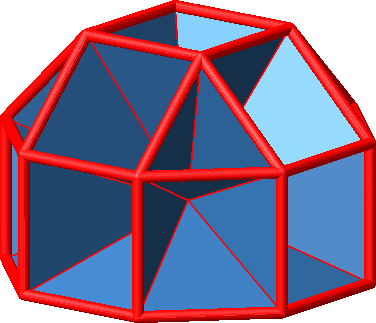
Abb. 4.59: Asymmetrisches Beispiel

Wir haben viermal n = 3, dreizehnmal n = 4 und einmal n = 8. Weiter ist:

Abb. 4.60: Zusammensetzung

Abb. 4.61: Osterei

Weblinks

Hans Walser: Kantenmodell des Würfels und des Tetraeders

http://www.walser-h-m.ch/hans/Miniaturen/K/Kantenmodell_Wuerfel/Kantenmodell_Wuerfel.htm

Hans Walser: Kuboktaeder-Kantenmodell

http://www.walser-h-m.ch/hans/Miniaturen/K/Kuboktaeder-Kantenmodell/Kuboktaeder-Kantenmodell.htm

Hans Walser: Kuboktaeder-Stern

http://www.walser-h-m.ch/hans/Miniaturen/K/Kuboktaeder-Stern/Kuboktaeder-Stern.html

Hans Walser: Langer Würfel

http://www.walser-h-m.ch/hans/Miniaturen/L/Langer_Wuerfel/Langer_Wuerfel.html

Hans Walser: Rhombendodekaeder

http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombendodekaeder/Rhombendodekaeder.htm

Hans Walser: Rhombendodekaeder

http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombendodekaeder2/Rhombendodekaeder2.htm

Hans Walser: Rhombendodekaeder aus zwölf Bauteilen

http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombendodekaeder3/Rhombendodekaeder3.htm

Hans Walser: Rhombendodekaederstern

http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombendodekaederstern/Rhombendodekaederstern.htm

Hans Walser: Rhombenfiguren

http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombenfiguren/Rhombenfiguren.htm

Hans Walser: Rhombenhexaeder

http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombenhexaeder2/Rhombenhexaeder2.html

Hans Walser: Rhombenhexaeder

http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombenhexaeder3/Rhombenhexaeder3.html

Hans Walser: Rhombentriakontaeder

http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombentriakontaeder/Rhombentriakontaeder.html

Hans Walser: Rhombic Dodecahedron in the Cube

http://www.walser-h-m.ch/hans/Miniaturen/R/Rhombic_Dodecahedron/Rhombic_Dodecahedron.htm

Hans Walser: Würfelstern

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelstern/Wuerfelstern.html