Hans Walser, [20220531]

Pyramide

Idee und Anregung: Maik Bleckmann, Bremen

1 Worum geht es?

Rekonstruktion einer Pyramide

2 Planimetrische Konstruktion

Wir beginnen mit einem Fächer von drei Strecken der Länge 1 und Zwischenwinkeln α (Abb. 1a).

Anschließend passen wir am unteren Ende einen Rhombus ein (Abb. 1b). Wir interpretieren nun die Figur als Bild einer räumlichen Pyramide (Abb. 1c und 2).

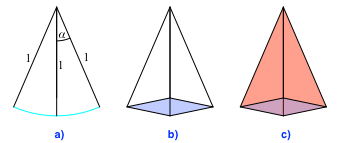
Abb. 1: Konstruktion

Die Abbildung 2 zeigt die zugehörige Animation.

Abb. 2: Animation

3 Pyramidendaten

Wir fragen nach den Ausmaßen der Pyramide der Abbildungen 1c und 2 unter der Annahme, dass es sich um eine gerade Pyramide mit quadratischer Grundfläche in einer orthografischen Parallelprojektion (Bildebene normal zur Projektionsrichtung, Normalaxonometrie) handelt. Dazu gleich ein Wort zur Vorsicht: Die wirklichen Längen der Pyramide im Raum werden bei dieser Projektion verkürzt. Die wirklichen Längen der schrägen Kanten sind also größer oder gleich eins, in der Regel größer als eins.

Um die wirklichen Längen zu sehen, gucken wir die Sache von der Seite an (Abb. 3b).

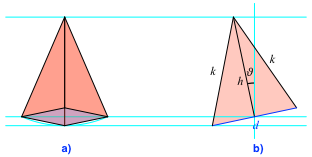
Abb. 3: Blick von vorne und von der Seite

In dieser Sicht von der Seite (sogenannter Seitenriss oder Kreuzriss) sehen wir die wirkliche Länge h der Pyramidenhöhe, die wirkliche Länge k der Schrägkanten und die wirkliche Länge d der Diagonale der quadratischen Grundfläche. Ebenso sehen wir, wie die Pyramide um den Winkel ϑ nach vorn gekippt ist. Für die Seitenlänge s der quadratischen Grundfläche erhalten wir:

Die Angaben s und h genügen, um die Pyramide zu rekonstruieren.

4 Variation von α

Die Abbildung 4 zeigt, wie sich die Situation bei Variation von α verändert.

Abb. 4: Variation von α

Mit der Vergrößerung des Winkels α wird auch der Kippwinkel ϑ vergrößert. Die Grundfläche der Pyramide wird entsprechend verdreht.

5 Formeln

Die relevanten Daten sowie das Volumen V der räumlichen Pyramide hängen wie folgt vom Winkel α ab:

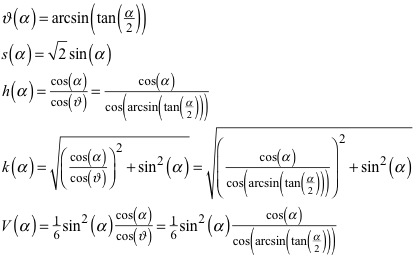
Herleitung: Trigonometrie

Wir sehen in der Formel für k(α), dass die Kantenlänge k nicht die Konstante 1 ist. Die Abbildung 5 zeigt den zugehörigen Funktionsgraf. Das Minimum 1 wird bei α_min = 0 angenommen, das Maximum 5/4 = 1.25 bei:

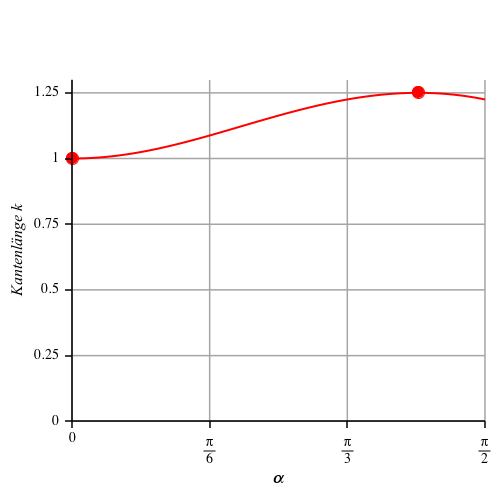
Abb. 5: Kantenlänge

Die Abbildung 6 zeigt die Pyramidenhöhe h in Abhängigkeit des Winkels α.

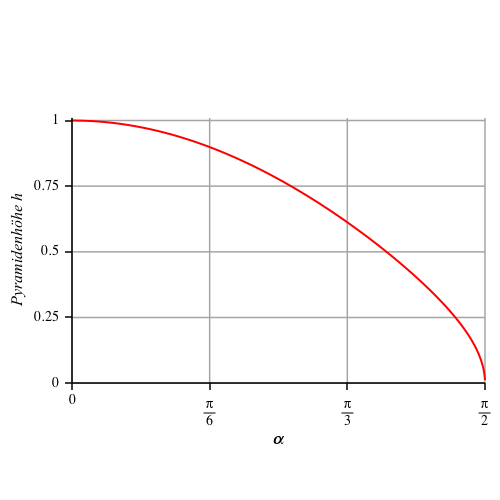
Abb. 6: Pyramidenhöhe

Die Abbildung 7 zeigt das Pyramidenvolumen V in Abhängigkeit des Winkels α. Das Maximum wird bei α = π/3 angenommen und beträgt:

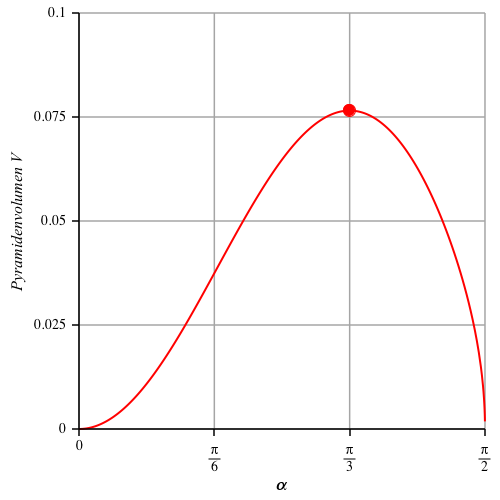
Abb. 7: Pyramidenvolumen

6 Die Pyramiden

In der Abbildung 8 zeigt die verschiedenen Pyramiden mit festbleibender Spitze in der immer gleichen Projektion. Es wird also gegenüber der Projektionsebene nichts verdreht.

Abb. 8: Pyramiden mit invarianter Spitze

In der Abbildung 9 bleibt die Grundebene der Pyramiden invariant. Die Spitze geht auf und ab.

Abb. 9: Invariante Grundebene

7 Sonderfälle

7.1 α = π / 4

Für α = π/4 wir s = 1.

7.2 α = π / 3

Für α = π/3 (Abb. 10) erhalten wir das maximale Volumen:

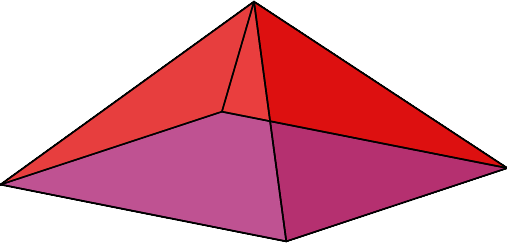
Abb. 10: Maximales Volumen

Weiter ist die Pyramidenhöhe h

und die Seitenlänge s der quadratischen Grundfläche:

Die Pyramidenhöhe h ist also halb so groß wie die Seitenlänge s der quadratischen Grundfläche. Daher lässt sich die Pyramide mit optimalem Volumen in einen Würfel so einpassen, dass die Spitze in der Würfelmitte liegt (Abb. 11). Es haben sechs solche Pyramiden Platz im Würfel.

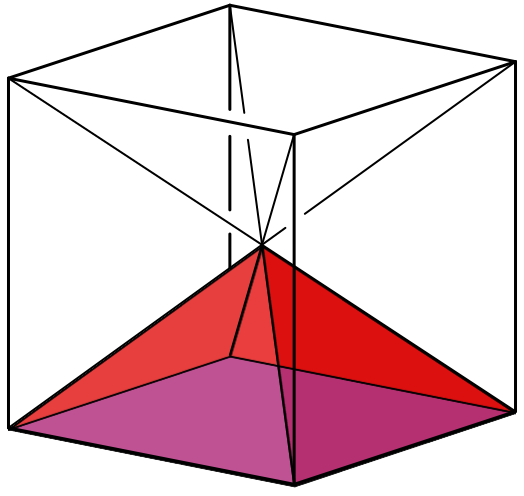
Abb. 11: Einpassen in den Würfel

Eine solche Pyramide lässt sich aus einem Papier im DIN-Format durch Falten herstellen.

Literatur

Bleckmann, Maik (2022): Pyramidenansatz zum Erstellen von Mustern (Manuskript)

Weblink

Hans Walser: Pyramide

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyramide/Pyramide.html

Hans Walser: Pyramidenoptimierung

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyramidenoptimierung2/Pyramidenoptimierung2.html

Hans Walser: Pyramidenoptimierung

http://www.walser-h-m.ch/hans/Miniaturen/P/Pyramidenoptimierung/Pyramidenoptimierung.htm

Hans Walser: Würfel aus sechs Bauteilen

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfel6/Wuerfel6.htm