Hans Walser, [20220601]
Pyramidenoptimierung
1 Problemstellung
Welche n-Seit- Pyramide mit gegebener Kantenlänge 1 hat den größten Volumeninhalt V ?
2 Beispiel
Die Abbildung 1 zeigt ein Beispiel für n = 5. Das Volumen wächst zuerst und nimmt dann wieder ab. Somit gibt es dazwischen ein Maximum.
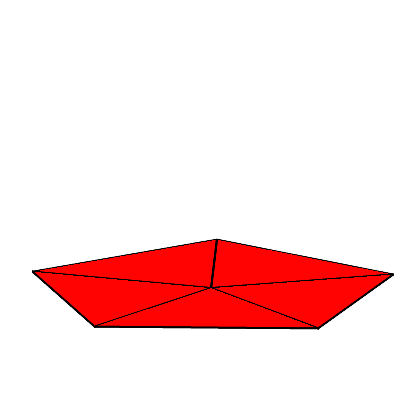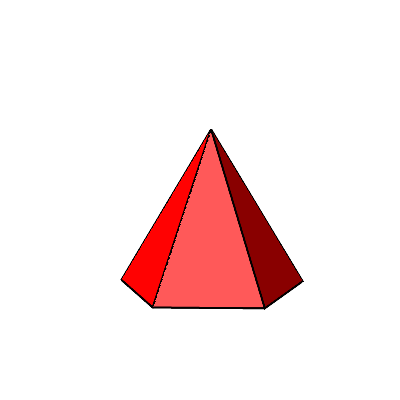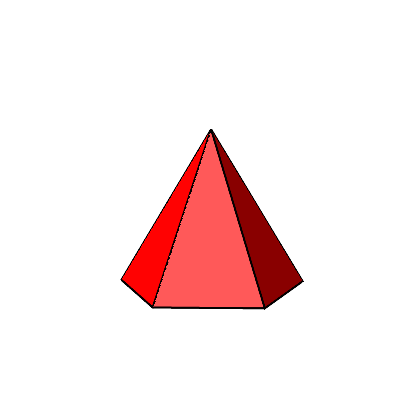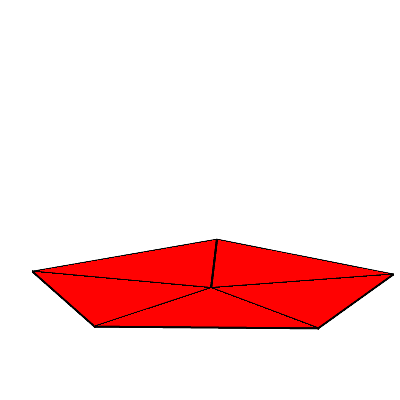
Abb. 1: Variables Volumen
3 Bearbeitung
Die Abbildung 2 zeigt für n = 5 die Bezeichnungen.

Abb. 2: Bezeichnungen
Wir wählen die Höhe h als Parameter der Optimierung. Es ist dann:
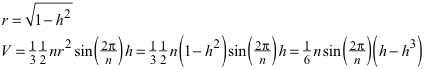
Der variable Koeffizient (h – h3) hat sein Maximum für (Herleitung mit Differentialrechnung wie in der Schule gelernt):
![]()
Für den Umkreisradius r des Boden-n-Eckes erhalten wir:
Die Abbildung 3 zeigt den optimalen Fall für n = 5.
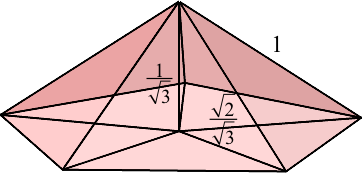
Abb. 3: Optimaler Fall
4 Bemerkungen
4.1 Unabhängigkeit von der Anzahl der Seitenflächen
Die optimalen Werte für h und r sind unabhängig von n. Die Abbildung 4 zeigt die optimale Lösung für n von 3 bis 30. Die Pyramidenspitze und eine Schrägkante bleiben invariant.

Abb. 4: Optimale Lösungen
4.2 DIN-Format
Die Höhe h und der Umkreisradius r stehen im Verhältnis h : r = 1 : √2. Das ist auch das Seitenverhältnis eines Rechteckes im DIN-Format (gelb in Abb. 5).
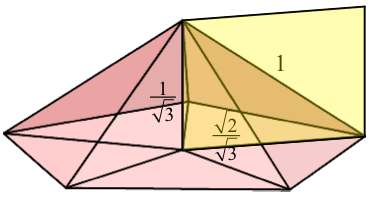
Abb. 5: DIN-Format
4.3 Sonderfälle
4.3.1 n = 3
Für n = 3 sind die Seitenflächen der Pyramide rechtwinklig gleichschenklige Dreiecke (Abb. 6). Zudem stehen die drei Seitenflächen paarweise senkrecht zueinander.
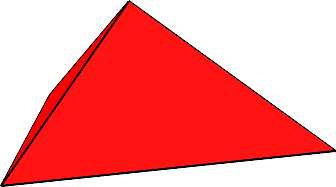
Abb. 6: Drei Seitenflächen
Die Pyramide ergibt sich auch durch Abschneiden einer Würfelecke (Abb. 7).

Abb. 7: Würfelecke abschneiden
Die Pyramide passt in ein Oktaeder (Abb. 8).

Abb. 8: Im Oktaeder
Insgesamt passen acht Pyramiden in das Oktaeder (Abb. 9). Diametral gegenüberliegende Pyramiden sind jeweils in derselben Farbe dargestellt.
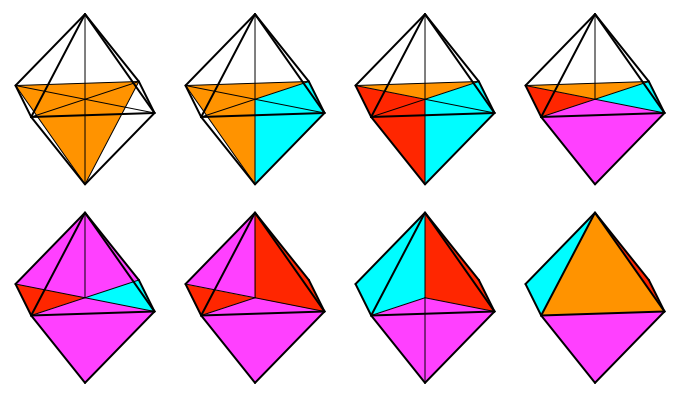
Abb. 9: Acht Pyramiden im Oktaeder
4.3.2 n = 4
Die Abbildung 10 zeigt die Situation für n = 4. Die Pyramidenhöhe ist genau halb so groß wie die Bodenkante. Zwei benachbarte Seitendreiecke schließen einen Winkel von 120° ein.
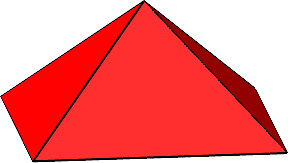
Abb. 10: Vier Seitenflächen
Pyramiden dieser Art können aus Papier im DIN-Format durch Falten hergestellt werden.
Die Pyramide kann in einen Würfel eingebaut werden, die Pyramidenspitze liegt im Würfelmittelpunkt (Abb. 11).
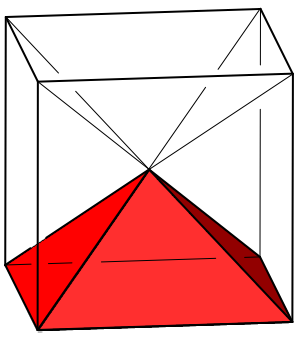
Abb.
11: Im Würfel
Es passen genau sechs Pyramiden in den Würfel (Abb. 12).
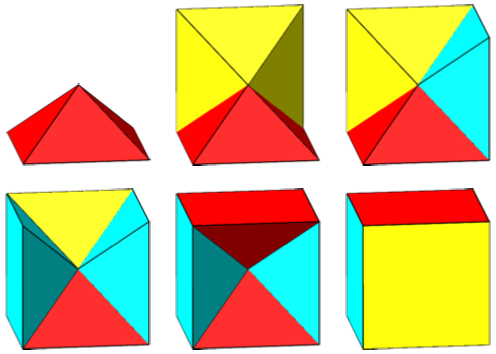
Abb. 12: Sechs Pyramiden
Literatur
Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.
Weblink
Hans Walser: Miniaturen: DIN-Format
http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/DIN_Format/index.html
Hans Walser: Pyramidenoptimierung
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyramidenoptimierung/Pyramidenoptimierung.htm
Hans Walser: Würfel aus sechs Bauteilen
http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfel6/Wuerfel6.htm