Hans Walser, [20221015]

Lemniskate

Anregung: K. H., Gö.

1 Worum geht es?

Spezielle Trapeze und Tangenten im Kontext der Lemniskate von Jacob Bernoulli. DIN-Format. Goldener Schnitt

2 Mechanisches Modell

Die Lemniskate von Jacob Bernoulli kann mit einem mechanischen Modell gezeichnet werden (Abb. 1). Das Modell besteht aus drei mit Gelenken verbundenen Stangen (magenta). Die beiden kurzen Stangen haben die Länge 1, die lange Stange die Länge √2. Die schwarzen Verankerungspunkte der beiden kurzen Stangen haben voneinander ebenfalls den Abstand √2. Der Schreibstift befindet sich in der Mitte der bewegten langen Stange.

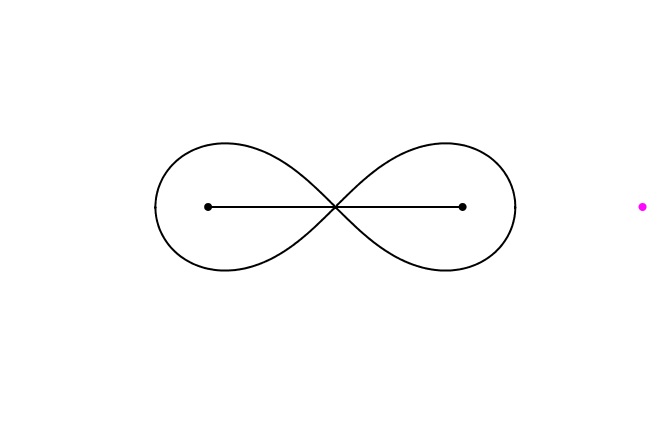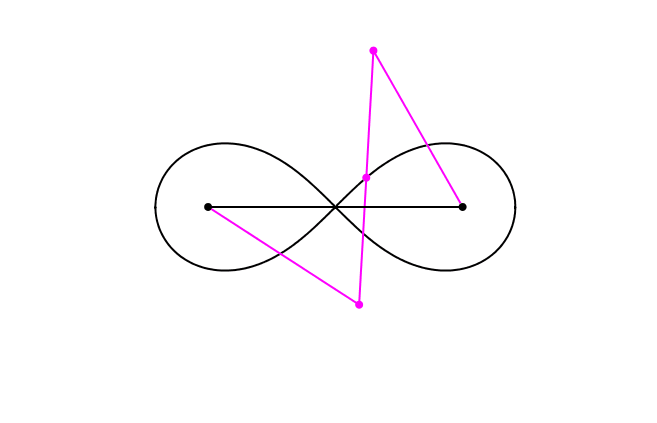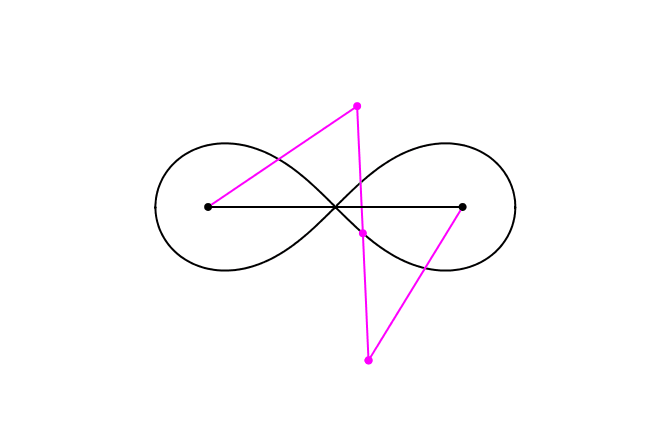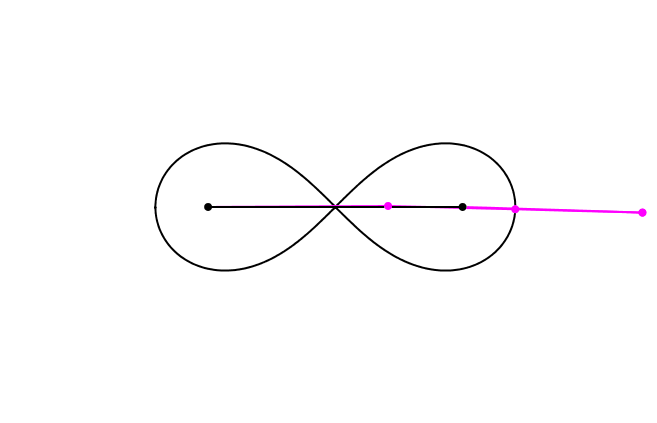
Abb. 1: Gelenkmodell

3 Gleichschenkliges Trapez

Das Gelenkmodell spannt ein gleichschenkliges Trapez auf (gelb in Abb. 2). Die beiden kurzen Stangen sind die Schenkel, die lange Stange und die Verbindung der Verankerungspunkte die Diagonalen des Trapezes.

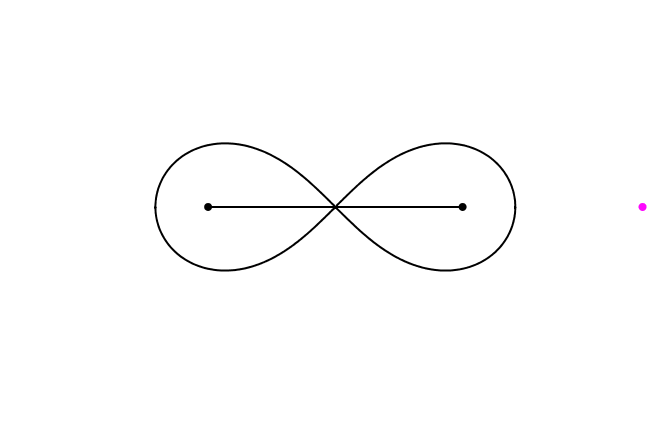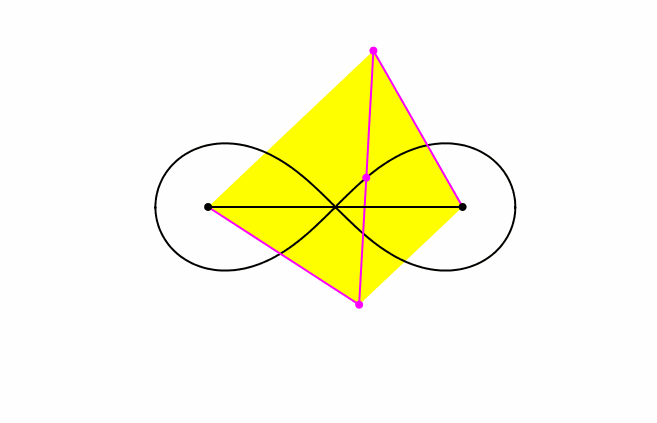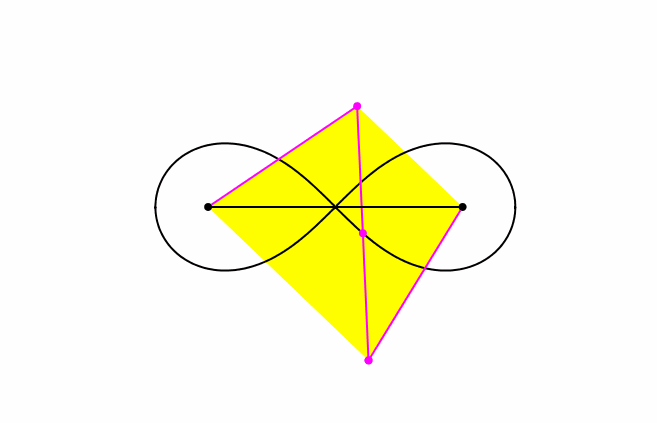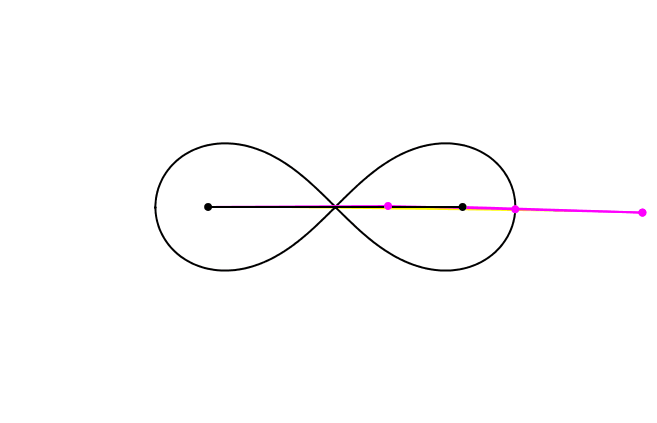
Abb. 2: Gleichschenkliges Trapez

Die beiden parallelen Seiten des Trapezes variieren in der Länge. Das Produkt der Längen ist aber 1. Die parallelen Seiten sind also Kehrwerte voneinander. Nachweis durch Rechnung.

4 Sonderfälle

Wir diskutieren drei Sonderfälle für das gelbe Trapez.

4.1 Quadrat

Wenn der Schreibstift über den Doppelpunkt der Lemniskate fährt, ist das gelbe Trapez ein Quadrat (Abb. 3). Die beiden Parallelseiten des Trapezes haben je die Länge 1.

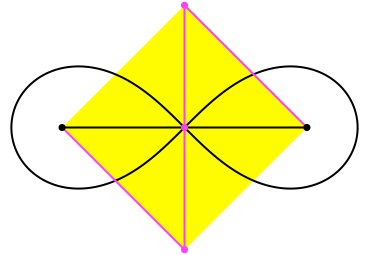
Abb. 3: Quadrat

4.2 DIN-Trapez

Das DIN-Trapez entsteht folgendermaßen. Wir falten ein Papier im DIN-Format, zum Beispiel DIN A4, längs einer Diagonale und nehmen die konvexe Hülle der Figur (Abb. 4).

Abb. 4: DIN-Trapez

Im DIN-Trapez schneiden sich die Diagonalen mit dem Winkel ω = arccos(1/3) ≈ 70.529°. Dies ist auch der Winkel, unter dem sich die Raumdiagonalen des Würfels schneiden. Weiter ist es der Winkel zwischen zwei benachbarten Seitenflächen des Tetraeders (Diederwinkel des Tetraeders). Sein Ergänzungswinkel 180° – ω ≈ 109.471° ist der Diederwinkel des Oktaeders. Diese beiden Winkel spielen in der Kristallografie eine wichtige Rolle.

Die lange Parallelseite des DIN-Trapezes hat die Länge √3, die kurze ein Drittel davon, also 1/√3.

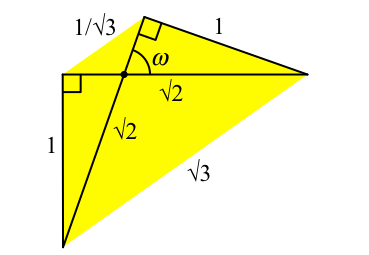
Abb. 5: Diagonalenschnittwinkel

Das DIN-Trapez können wir in die Lemniskate einbetten (Abb. 6). Der Mittelpunkt der einen Diagonalen ist im Doppelpunkt der Lemniskate, der Mittelpunkt der anderen Diagonalen liegt auf der Lemniskate.

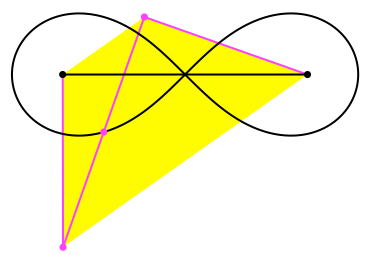
Abb. 6: DIN-Trapez und Lemniskate

Der Gag ist nun folgendes: Die Tangente im so konstruierten Punkt der Lemniskate verläuft durch einen der beiden schwarzen Verankerungspunkte (Abb. 7). Mit DGS erhärtet.

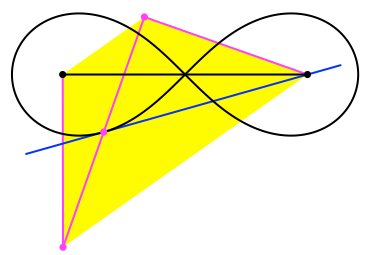
Abb. 7: Tangente

4.3 Goldenes Trapez

Das Goldene Trapez ist definiert wie folgt. Es ist gleichschenklig. Die Basiswinkel sind 60°, die Schenkellänge 1 und die Diagonalenlänge √2 (Abb. 8).

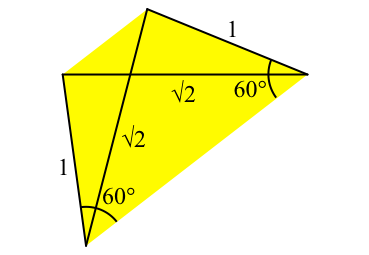
Abb. 8: Goldenes Trapez

Die Parallelseiten haben die Längen Φ = (1 + √5)/2 ≈ 1.618 (Goldener Schnitt) und 1/Φ = (–1 + √5)/2 ≈ 0.618. Daher der Name Goldenes Trapez.

Wir passen nun das Goldene Trapez in die Lemniskate ein (Abb. 9).

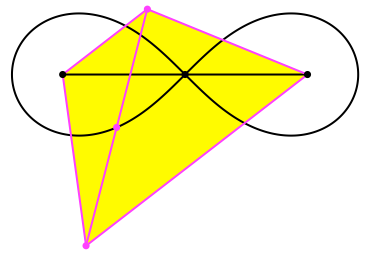
Abb. 9: Lemniskate und Goldenes Trapez

Der Mittelpunkt der magenta Diagonale liegt auf der Lemniskate.

Wir zeichnen nun zusätzlich das an der senkrechten Symmetrieachse der Lemniskate gespiegelte Goldene Trapez ein (rot in Abb. 10). Die Tangente im Lemniskatenpunkt verläuft durch den Diagonalenschnittpunkt des gespiegelten Trapezes. Mit DGS erhärtet.

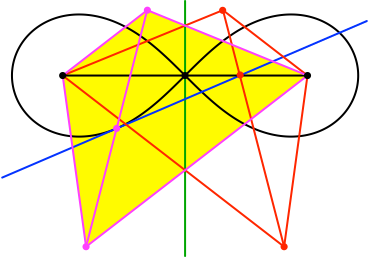
Abb. 10: Gespiegeltes Trapez. Tangente

Das gilt natürlich auch umgekehrt (Abb. 11).

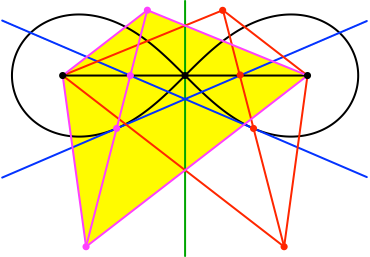
Abb. 11: Gespiegelte Tangente

Websites

Klaus-Anton’s Blog: Draw the Lemniscate of Bernoulli

https://artofproblemsolving.com/community/c2083h2928828_draw_the_lemniscate_of_bernoulli_in_asy

Hans Walser: Winkeldrittelung mit Lemniskate

www.walser-h-m.ch/hans/Miniaturen/W/Winkeldrittelung5/Winkeldrittelung5.htm

Hans Walser: Lemniskate

http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate/Lemniskate.htm

Hans Walser: Lemniskate

http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate2/Lemniskate2.htm

Hans Walser: Lemniskate

http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate3/Lemniskate3.htm

Hans Walser: Lemniskatoid

http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskatoid/Lemniskatoid.htm

Hans Walser: Lemniskate als Enveloppe von Kreisen

http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate4/Lemniskate4.htm

Literatur

Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.

Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.

Walser, Hans (2018): Die Acht in der Kugel. MU, Der Mathematikunterricht. Jahrgang 64. Heft 4-2018. S. 50-55. ISSN 0025-5807.