1 Problemstellung

Über den Höhen eines beliebigen spitzwinkligen Dreiecks zeichnen wir je einen Halbkreis (grün in Abb. 1). Vom Höhenschnittpunkt ausgehend zeichnen wir zu jeder Höhe eine Lotstrecke bis zum zugehörigen Halbkreis (rot in Abb. 1).

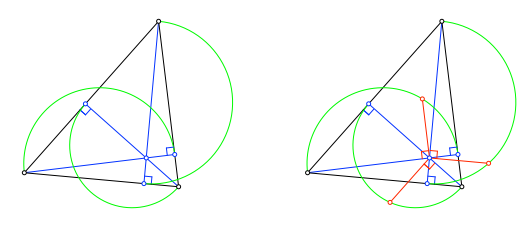
Abb. 1: Problemstellung

Die drei roten Lotstrecken sind gleich lang. Dies ist zu zeigen.

2 Beweise

2.1 Satz des Thales

Ein Beweis, der lediglich den Satz des Thales benötigt, spielt im Raum.

Wir zeichnen über zweien der drei Dreiecksseiten je die Thaleskugel, also eine Kugel mit der jeweiligen Dreiecksseite als Durchmesser. Die Abbildung 2 zeigt die Situation von oben.

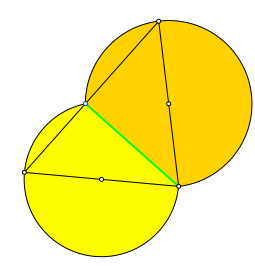
Abb. 2: Thaleskugeln. Sicht von oben

Die beiden Thaleskugeln schneiden sich in einem Kreis (grün), welcher senkrecht zur Dreiecksebene steht und eine Dreieckshöhe als Durchmesser hat. Die Abbildung 3 zeigt die obere Hälfte dieses Kreises in einer Ansicht. Über dem Höhenschnittpunkt ist zusätzlich die Lotstrecke (Lot zur Dreiecksebene) bis zum Halbkreis gezeichnet. Diese Lotstrecke ist gleich lang wie das Lot auf die entsprechende Höhe in der Abbildung 1 der Problemstellung.

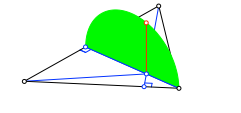
Abb. 3: Ansicht

Nun bringen wir noch die Thaleskugel der dritten Dreieckseite ins Spiel. Diese drei Thaleskugeln haben zwei Punkte gemeinsam, welche spiegelbildlich zur Dreiecksebene oberhalb und unterhalb des Höhenschnittpunktes liegen.

Die rote Lotstrecke ist für alle drei Höhen dieselbe. Dies war zu zeigen.

Bemerkung: Die Verbindungen von einem der beiden Schnittpunkte zu den Dreiecksecken ergeben ein orthogonales Dreibein (Abb. 4). Dies folgt aus der Konstruktion mit den Thaleskugeln.

Abb. 4: Orthogonales Dreibein

2.2 Planimetrischer Beweis

Der nachfolgende planimetrische Beweis benötigt die Ähnlichkeit und den Höhensatz.

Wir können mit zwei Dreieckshöhen zwei ähnliche rechtwinklige Dreiecke definieren (Abb. 5). Die Ähnlichkeit ergibt sich aus der Gleichheit von je zwei Dreieckswinkeln.

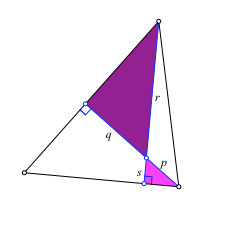
Abb. 5: Ähnliche Dreiecke

Aus der Ähnlichkeit ergibt sich mit den Bezeichnungen der Abbildung 5:

p/s = r/q

Daraus erhalten wir: pq = rs

Die Produkte der Höhenabschnitte sind also gleich. Wegen zyklischer Vertauschung gilt das auch mit Einbezug der dritten Höhe.

Satz: Das Produkt der Höhenabschnitte ist eine Invariante.

Bemerkung 1: Mathematik ist das Finden von Invarianten (Heinz Hopf).

Bemerkung 2: Der Satz gilt auch für das stumpfwinklige Dreieck. Im rechtwinkligen Dreieck ist die Invariante null.

Wir interpretieren nun die Höhenabschnitte als Hypotenusenabschnitte von rechtwinkligen Dreiecken (Abb. 6).

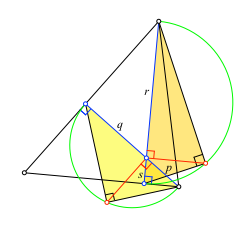
Abb. 6: Hypotenusenabschnitte

Nach dem Höhensatz sind die Höhen dieser rechtwinkligen Dreiecke die Quadratwurzeln aus den Hypotenusenprodukten, also ebenfalls invariant. Diese Höhen sind die roten Lotstrecken der Problemstellung (Abb. 1). Deren Längen sind also gleich. Dies war zu zeigen.

Weblinks

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte4/Hoehenabschnitte4.html

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte3/Hoehenabschnitte3.html

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte2/Hoehenabschnitte2.html

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte/Hoehenabschnitte.htm