Hans Walser, [20230524]

Höhenabschnitte

Anregung: Hans Humenberger, Wien

1 Worum geht es?

Rechnerische Behandlung eines elementargeometrischen Problems.

2 Problemstellung

Ein Dreieck ABC habe den Höhenschnittpunkt H und die Höhenabschnitte (von H zu den Ecken) AH, BH, CH.

Gegeben seien die Höhenabschnitte, gesucht ist das Dreieck.

3 Spitzwinkliges Dreieck

Wir behandeln zunächst den spitzwinkligen Fall.

3.1 Vom Dreieck zum Sechseck

Die Abbildung 1 zeigt ein spitzwinkliges Dreieck mit den drei farbig markierten Höhenabschnitten.

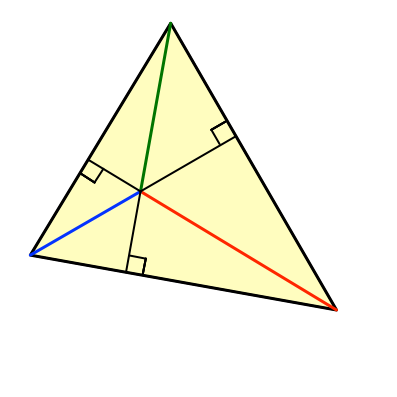
Abb. 1: Höhenabschnitte im Dreieck

Im hellblauen Viereck (Abb. 2) haben wir zwei gegenüberliegende rechte Winkel. Daher ergänzen sich die beiden anderen Winkel auf 180°.

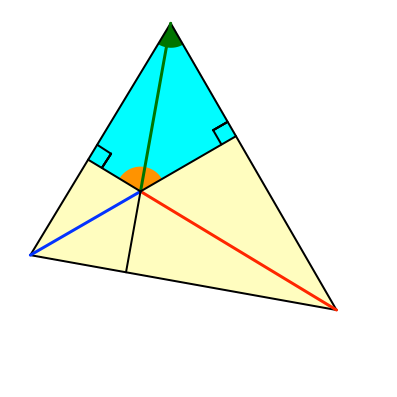
Abb. 2: Ergänzungswinkel

Diesen Ergänzungswinkel können wir weiterverfolgen (Abb. 3 und 4).

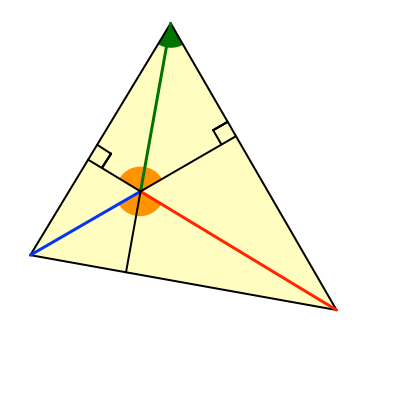
Abb. 3: Punktgespiegelter Ergänzungswinkel

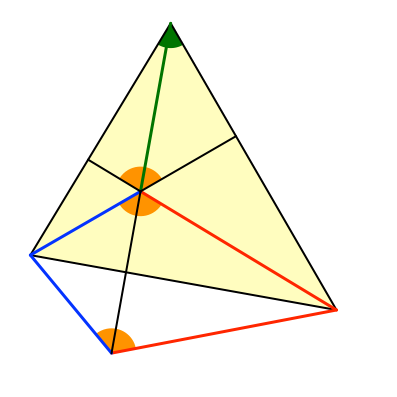
Abb. 4: Herausgeklappter Ergänzungswinkel

Nun haben wir aber ein Sehnenviereck (Abb. 5). Der herausgespiegelte Höhenschnittpunkt liegt auf dem Umkreis des Dreiecks.

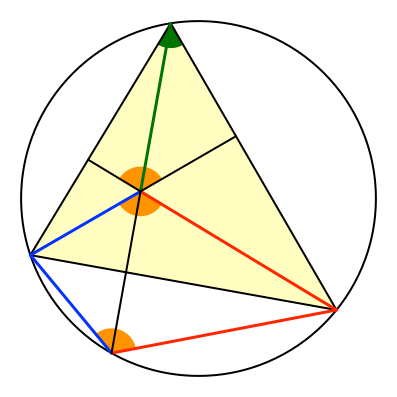
Abb. 5: Sehnenviereck

Analog können wir an den beiden anderen Seiten herausspiegeln (Abb. 6).

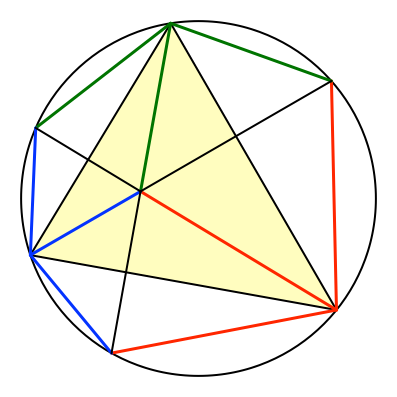
Abb. 6: Vollständiges Herausspiegeln

Wir erhalten ein Sehnensechseck. Sein Umkreis ist der Umkreis des Dreieckes, seine Seiten sind paarweise die Höhenabschnitte, in unserer Färbung also rot-rot-grün-grün-blau-blau (Abb. 7).

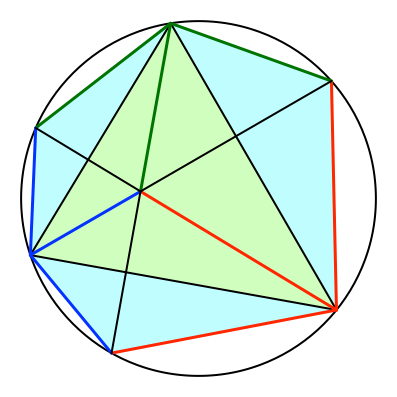
Abb. 7: Sehnensechseck

Wir kennen die Seiten des Sechseckes, nicht aber den Radius des Umkreises. Dazu eine rechnerische Behandlung.

3.2 Rechnerische Behandlung

Wir arbeiten mit den Bezeichnungen der Abbildung 8.

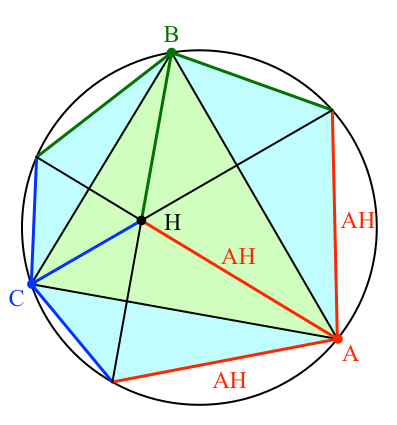
Abb. 8: Bezeichnungen

Der Trick besteht nun darin, das Sechseck in sechs gleichschenklige Sektordreiecke aufzuteilen (Abb. 9).

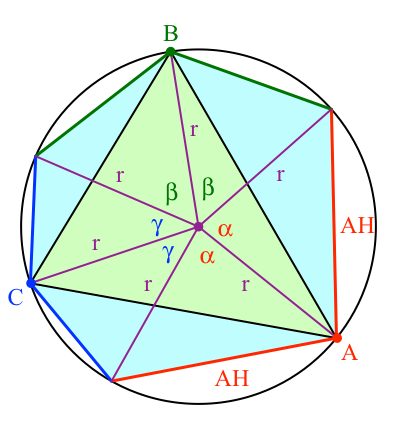
Abb. 9: Sektordreiecke

Nun ist:

Da die Summe der Winkel im Zentrum 2π ist, ergibt sich für den Umkreisradius r die Bedingung:

Diese Gleichung lösen wir mit CAS (Maple) nach r auf.

3.3 Beispiel

Wir arbeiten exemplarisch mit den Daten (vgl. Abb. 1 bis 9): AH = 8.08, BH = 6.02, CH = 4.49.

restart: with(plots): with(plottools): local gamma:

AH := 8.08:

BH := 6.02:

CH := 4.49:

Gleichung:= arcsin(AH/2/r) + arcsin(BH/2/r) + arcsin(CH/2/r) = Pi/2:

Loesung := solve(Gleichung, r):

r := Loesung;

Das Ergebnis ist r = 6.256851454.

Um die Figur sichtbar zu machen, fahren wir im Programm fort:

Umkreis := circle([0,0], r, thickness = 2, color = black):

alpha := 2*arcsin(AH/2/r):

beta := 2*arcsin(BH/2/r):

gamma := 2*arcsin(CH/2/r):

xA := r: yA := 0: A := [xA,yA]:

xB := r*cos(alpha + beta): yB := r*sin(alpha + beta): B := [xB,yB]:

xC := r*cos(alpha + 2*beta + gamma): yC := r*sin(alpha + 2*beta + gamma): C := [xC,yC]:

Punkt := proc(A, Farbe) local Punkt :

Punkt := point(A, symbol = solidcircle, symbolsize = 15, color = Farbe):

end proc:

Linie := proc(A, B, Farbe)local Linie :

Linie := line(A, B, thickness = 3, color = Farbe):

end proc:

xH := ((-yB + yC)*yA^2 + (yB^2 - yC^2 - (xB - xC)*xA)*yA - yB^2*yC + (yC^2 + (xA - xC)*xB)*yB - xC*yC*(xA - xB))/((-xB + xC)*yA + (xA - xC)*yB - yC*(xA - xB)):

yH := ((xB - xC)*xA^2 + (-xB^2 + xC^2 + yA*(yB - yC))*xA + xB^2*xC + (-xC^2 - yB*(yA - yC))*xB + xC*yC*(yA - yB))/((yB - yC)*xA + (-yA + yC)*xB + xC*(yA - yB)):

H := [xH, yH]:

TextA := textplot([xA,yA,"A"], color = red, font=[Times, 24, roman],'align' = {'above', 'right'}):

TextB := textplot([xB,yB,"B"], color = COLOR(RGB, 0, 0.5,0), font=[Times, 24, roman],'align' = {'above', 'right'}):

TextC := textplot([xC,yC,"C"], color = blue, font=[Times, 24, roman],'align' = {'above', 'right'}):

TextH := textplot([xH,yH,"H"], color = black, font=[Times, 24, roman],'align' = {'above', 'right'}):

display([Umkreis, Linie(B, C, black), Linie(C, A, black), Linie(A, B, black), Linie(A, H, red), Linie(B, H, COLOR(RGB, 0, 0.5,0)), Linie(C, H, blue), TextA, TextB, TextC, TextH, Punkt(A, red), Punkt(B, COLOR(RGB, 0, 0.5,0)), Punkt(C, blue), Punkt(H, black)],

scaling=constrained,

axes = normal);

Die Abbildung 10 zeigt die ausgegebene Figur. Sie entspricht bis auf die Lage den Abbildungen 1 bis 9.

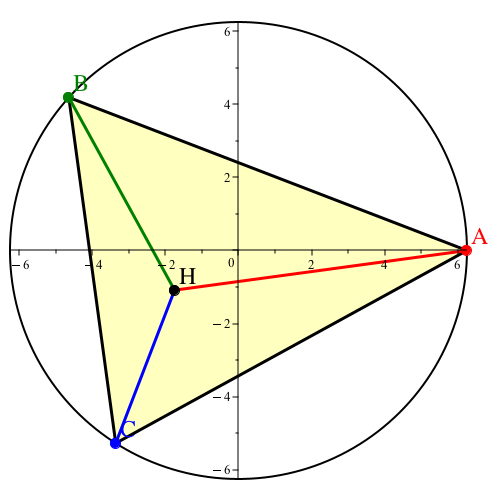
Abb. 10: Lösung im spitzwinkligen Fall

4 Stumpfwinkliges Dreieck

4.1 Vom Dreieck zum Sechseck

Die Abbildung 11 zeigt ein stumpfwinkliges Dreieck. Der Höhenschnittpunkt und die Höhenabschnitte liegen außerhalb des Dreiecks. Man beachte, dass die Höhenabschnitte gleich lang sind wie in der Abbildung 1.

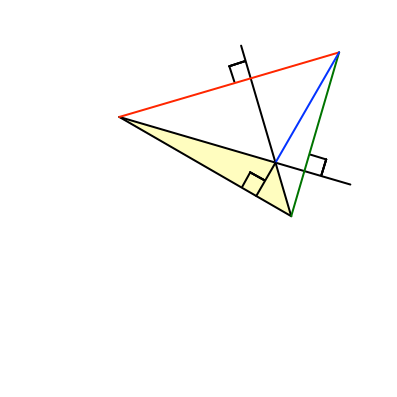
Abb. 11: Stumpfwinkliges Dreieck mit Höhenschnittpunkt

Wir zeichnen auch noch den Umkreis (Abb. 12).

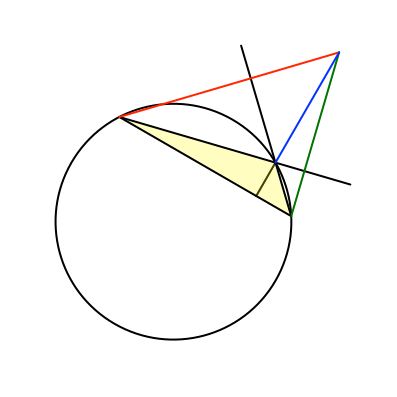
Abb. 12: Umkreis

Und nun spiegeln wir den Höhenschnittpunkt mit den Höhenabschnitten schrittweise an den drei Dreiecksseiten (Abb. 13 bis 15).

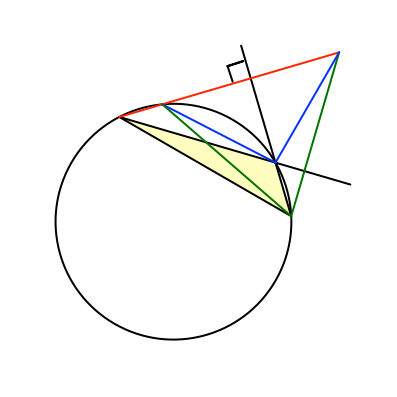
Abb. 13: Spiegeln an der ersten Seite

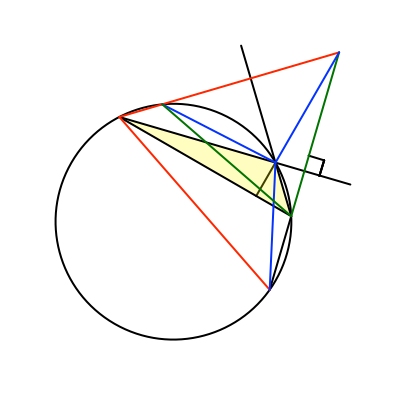
Abb. 14: Spiegeln an der zweiten Seite

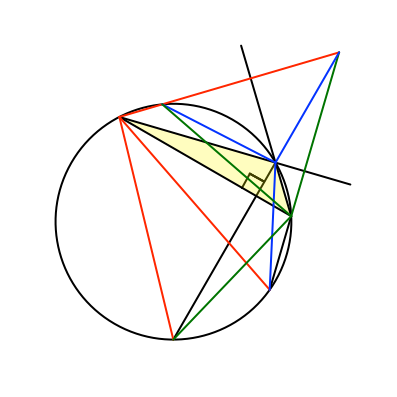
Abb. 15: Spiegeln an der dritten Seite

Die Spiegelpunkte des Höhenschnittpunktes liegen auf dem Umkreis. Wir erhalten im Umkreis eine Sehnensechseck, dessen Seiten je zwei Paare von Höhenabschnitten sind (Abb. 16 und 17). Es handelt sich um ein „überschlagenes“ Sechseck. Die Seiten überschneiden sich.

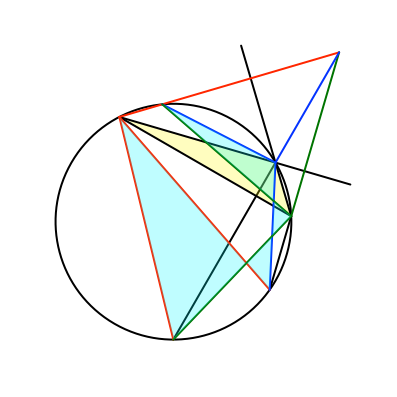
Abb. 16: Sehnensechseck

Abb. 17: Überschlagenes Sechseck

In unserer Problemstellung kennen wir die Seiten des Sehnensechseckes, nicht aber den Radius des Umkreises. Dazu eine rechnerische Behandlung.

4.2 Rechnerische Behandlung

Der Trick besteht nun darin, das Sechseck in sechs gleichschenklige Sektordreiecke aufzuteilen (Abb. 18). Die Sektordreiecke überlappen sich teilweisee.

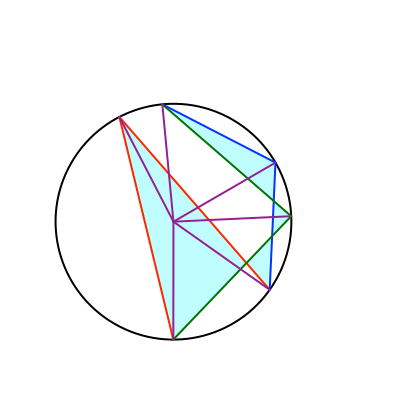
Abb. 18: Sektordreiecke

Wir arbeiten mit den Bezeichnungen der Abbildung 19.

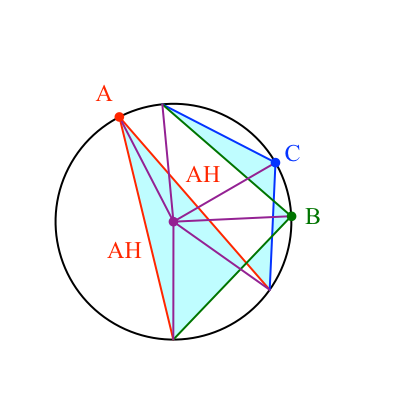
Abb. 19: Bezeichnungen

Die Frage der Winkel am Umkreismittelpunkt ist wegen der teilweisen Überlappung subtil. Wir zeigen das schrittweise (Abb. 20 bis 22). Wenn wir von 0 über 1 = A nach 2 gehen, drehen wir um einen Winkel von 2α (Abb. 20). Das sind die Spitzenwinkel der gleichschenkligen Sektordreiecke mit der roten Basis AH.

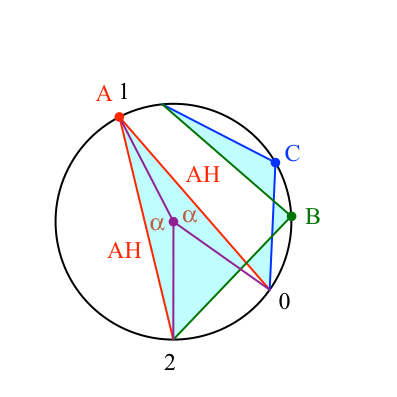
Abb. 20: 2 alpha

Wenn wir von 2 über 3 = B nach 4 gehen, drehen wir weiter um einen Winkel von 2β (Abb. 21). Das sind die Spitzenwinkel der gleichschenkligen Sektordreiecke mit der grünen Basis BH.

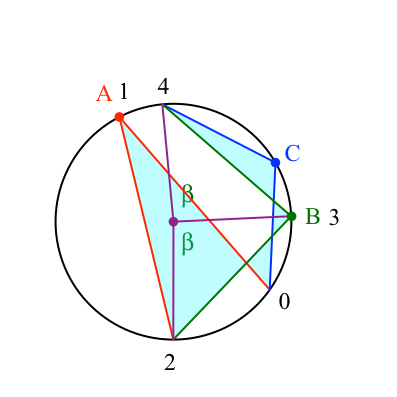
Abb. 21: 2 beta

Und jetzt wird es spannend. Bei den gleichschenkligen Sektordreiecken mit der blauen Basis CH geht es zurück. Wir drehen auf dem Weg von 4 über 5 = C nach 6 (beziehungsweise 0) um den Winkel 2γ zurück (Abb. 22).

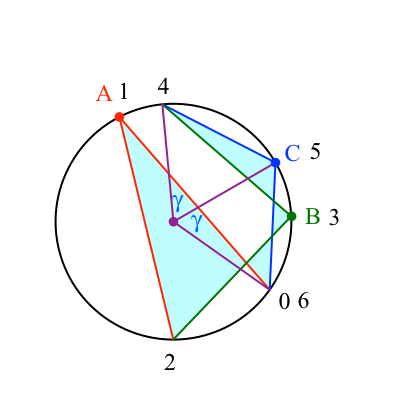
Abb. 22: minus 2 gamma

Die Summe aller Drehungen ist nun 2α + 2β – 2γ = 360° = 2π.

Nun ist:

Da die mit den richtigen Vorzeichen versehene Summe der Winkel im Zentrum 2π ist, ergibt sich für den Umkreisradius r die Bedingung:

Diese Gleichung lösen wir mit CAS (Maple) nach r auf.

4.3 Beispiel

Wir arbeiten wieder mit den Daten: AH = 8.08, BH = 6.02, CH = 4.49.

Für den Umkreisradius erhalten wir zwei Lösungen, nämlich r = 4.158271545 und r = 2.098579910.

Die Abbildung 23 zeigt die zu r = 4.158271545 gehörige Figur. Sie entspricht bis auf die Lage der Abbildung 11.

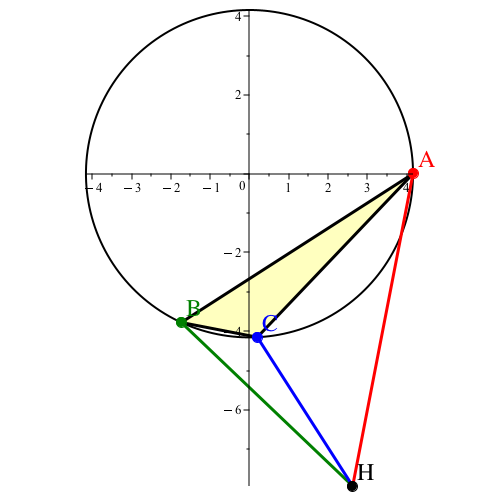
Abb. 23: Lösung

Für r = 2.098579910 erhalten wir komplexe Winkel:

α = 3.141592654 – 2.545198458 i

β = 3.141592654 – 1.802368916 i

γ = 3.141592654 – 0.7428295424 i

Es gibt kein Dreieck.

5 Rechtwinkliges Dreieck

Im rechtwinkligen Dreieck sind zwei Höhenabschnitte gleich je einer Kathete und der dritte null.

Im Beispiel mit den Daten AH = 4, BH = 3, CH = 0 ergibt sich das Lehrerdreieck (Abb. 24).

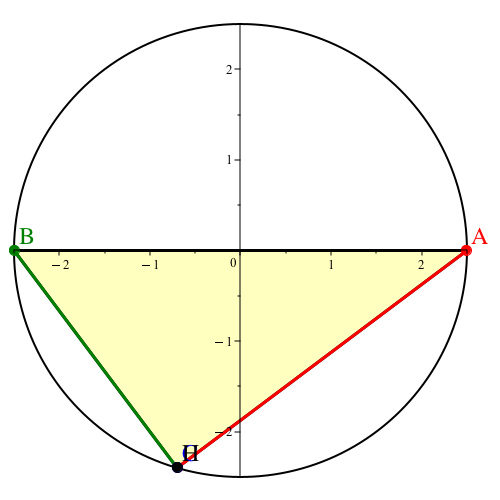
Abb. 24: Rechtwinkliges Dreieck

Weblinks

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte3/Hoehenabschnitte3.html

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte2/Hoehenabschnitte2.html

Hans Walser: Höhenabschnitte

http://www.walser-h-m.ch/hans/Miniaturen/H/Hoehenabschnitte/Hoehenabschnitte.htm