Hans Walser, [20220220]
Herzkurve
Idee und Anregung: Klaus-Anton’s Blog
1 Worum geht es?
Zwei herzförmige Kurven
2 Gleichschenkliges Dreieck
Wir halten bei einem gleichschenkligen Dreieck einen Schenkel fest und verdrehen den anderen (Abb. 1).
Für allfällige Berechnungen setzen wir die Schenkellänge 1 und die Spitze des gleichschenkligen Dreieckes in den Koordinatenursprung.

Abb. 1: Gleichschenkliges Dreieck
Nun kann man die Bahnkurven irgendwelcher „spezieller Punkte“ im Dreieck studieren.
3 Inkreis
In der Abbildung 2 ist der Inkreis mit den drei Berührungspunkten eingetragen. Der Berührungspunkt auf dem festgehaltenen Schenkel fährt hin- und her. Der Berührungspunkt auf der Basis des Dreiecks beschreibt den Thaleskreis über dem festgehaltenen Schenkel. Und was ist die Bahnkurve des roten Berührungspunktes auf dem gedrehten Schenkel (Abb. 3)?

Abb. 2: Inkreis

Abb. 3: Bahnkurve des roten Punktes
4 Inkreis-Herzkurve
Die Inkreis-Herzkurve (Abb. 4) hat die Polardarstellung:
![]() (1)
(1)
Ihre Bogenlänge s ist:
s = 4-2*5^(1/2)+8/3*3^(1/2)*arcsin(1/4)+4/9*3^(1/2)*Pi ≈ 3.113343306
Der Flächeninhalt A ist:
A = –4+3/2*Pi ≈ 0.712388981
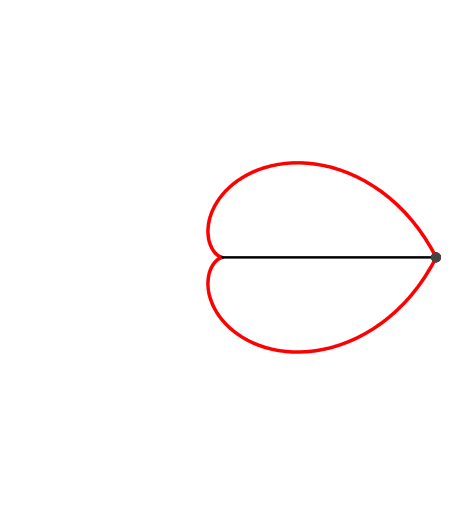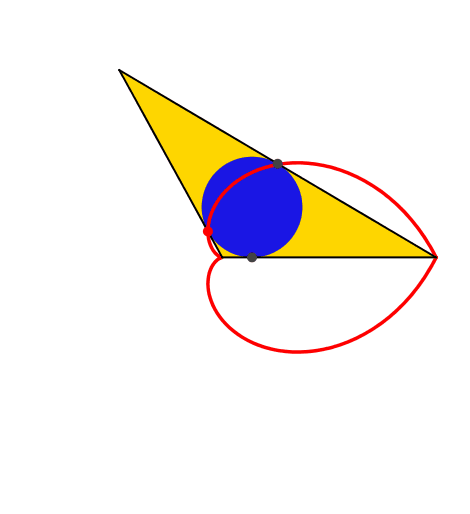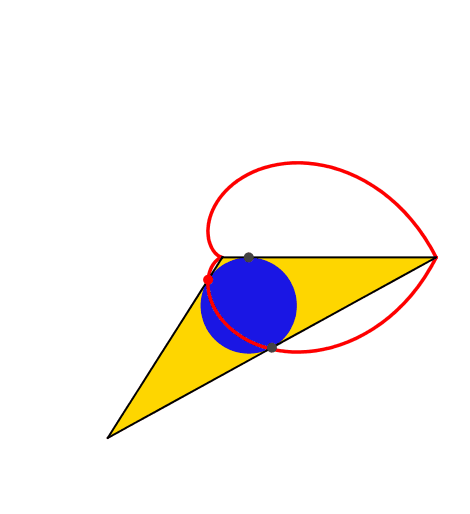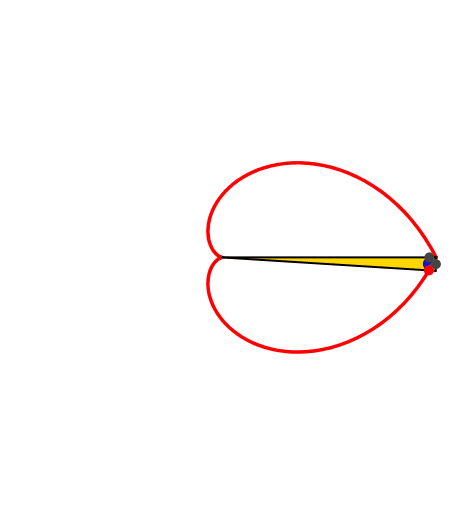
Abb. 4: Inkreis-Herzkurve
5 Ankreis-Herzkurve
Wir spiegeln den roten Punkt am Mittelpunkt eines Schenkels. Der hellblaue Spiegelpunkt ist der Berührungspunkt des Ankreises über diesem Schenkel. Seine Bahnkurve erinnert an die klassische Kardioide, ist sie aber nicht. Sie hat die Polardarstellung:
![]() (2)
(2)
Ihre Bogenlänge s ist ein elliptisches Integral mit dem numerischen Wert s ≈ 4.844224108.
Der Flächeninhalt A ist:
A = 1/2*Pi ≈ 1.570796327
Das ist die Hälfte des Flächeninhaltes des Einheitskreises.

Abb. 5: Ankreis-Herzkurve
6 Die beiden Kurven

Abb. 6: Die beiden Kurven
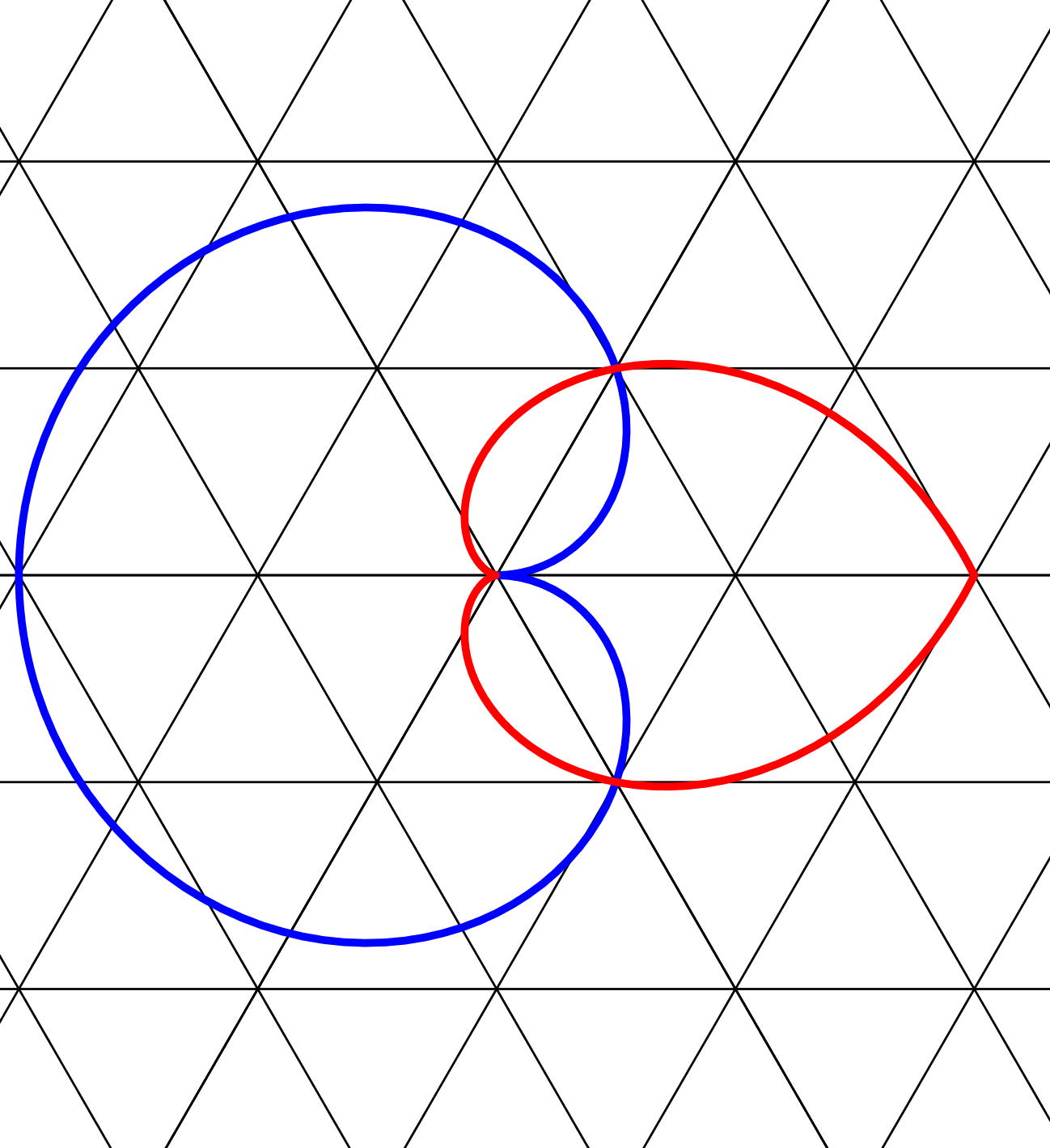
Abb. 7: Die beiden Kurven im Dreiecksraster
Die Schnittpunkte der beiden Kurven sind Rasterpunkte des Dreiecksrasters.
7 Winkel
Der Innenwinkel rechts bei der roten Inkreis-Herzkurve misst:
![]() (3)
(3)
Leider kein „schöner“ Winkel. Oder vielleicht doch. Die Hälfte davon, also der Winkel zur Horizontalen ist:
![]() (4)
(4)
Das ist der äußere Diederwinkel des regelmäßigen Dodekaeders.
Websites
Klaus-Anton’s Blog:
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve/Herzkurve.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve2/Herzkurve2.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve3/Herzkurve3.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve4/Herzkurve4.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve5/Herzkurve5.htm
Hans Walser: Herzkurve
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve6/Herzkurve6.html
Hans Walser: Die Herzkurve und die Möndchen des Hippokrates
www.walser-h-m.ch/hans/Miniaturen/H/Herzkurve_u_Hippokrates/Herzkurve_u_Hippokrates.htm
Hans Walser: Herzkurven
http://www.walser-h-m.ch/hans/Miniaturen/H/Herzkurven/Herzkurven.htm