Hans Walser, [20220810]

Würfelpuzzle

1 Problemstellung

Die sechs Quadrate (Abb. 1) sollen zu einem Würfel zusammengebaut werden. Wie viele Möglichkeiten gibt es?

Abb. 1: Sechs Quadrate

Die Abbildungen 2 bis 4 zeigen ein Beispiel in verschiedenen Darstellungsarten.

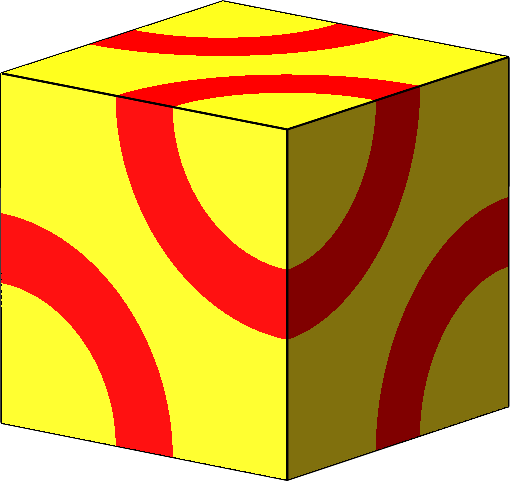
Abb. 2: Beispiel

Abb. 3: Beispiel von allen Seiten

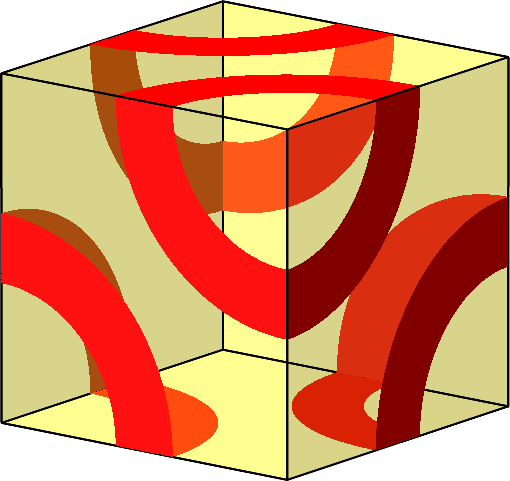
Abb. 4: Transparente Darstellung

2 Bearbeitung

Jedes Quadrat kann auf zwei Arten (Abb. 5) auf eine Würfelseite appliziert werden.

Abb. 5: Zwei Arten

Um sich ein Bild über die verschiedenen Möglichkeiten zu machen, können die sechs Quadrate der Abbildung 1 auf Karton aufgezogen und drehbar auf einen Holzwürfel geschraubt werden (Abb. 6). Durch Verdrehen der Quadrate um Vielfache von 90° ergeben sich die verschiedenen Möglichkeiten.

Abb. 6: Abgegriffenes Modell

3 Kombinatorik

Da also jedes Quadrat auf zwei Arten auf eine Würfelseite appliziert werden kann, gibt es 2⁶ = 64 Möglichkeiten (Abb. 7 und 8).

Abb. 7: Die 64 Möglichkeiten

Wir nummerieren die Möglichkeiten zeilenweise, links oben beginnend, mit 0 bis 63.

Abb. 8: Die 64 Möglichkeiten, sequentielle Darstellung

4 Würfelsymmetrien

In der Abbildung 7 sind die erste Möglichkeit links oben und die letzte Möglichkeit rechts unten gleich. Sie gehen durch eine Drehung des Würfels um eine Mittelachse um 90° auseinander hervor. Allgemein haben wir wegen der Symmetrien des Würfels viele Beispiele von gleichen Möglichkeiten.

Die Abbildung 9 gibt eine Übersicht. Die Anordnung entspricht der Abbildung 7. Jedes Feld enthält die Laufnummer dezimal und im sechsstelligen Binärcode sowie die Klassenangabe der gleichen Möglichkeiten.

Abb. 9: Übersicht

Bei Beispielen, die gegenüber dem blauen Mittelpunkt spiegelbildlich liegen, addieren sich die Laufnummern auf 63 und die Binärcodes auf 111111. Wir haben eine komplementäre Punktsymmetrie.

Jede Klasse enthält diejenigen Möglichkeiten, welche durch eine Bewegung (Drehung) ineinander übergeführt werden können. Es gibt acht Klassen (damit ist die Problemstellung beantwortet) mit den Häufigkeiten der Tabelle 1.

Klasse	A	B	C	D	E	F	G	H	total
Häufigkeit	2	12	6	24	6	6	4	4	64

Tab. 1: Klassen und Häufigkeiten

Die Abbildung 10 zeigt zu jeder Klasse den ersten Repräsentanten.

Abb. 10.A: Vier Bogendreiecke

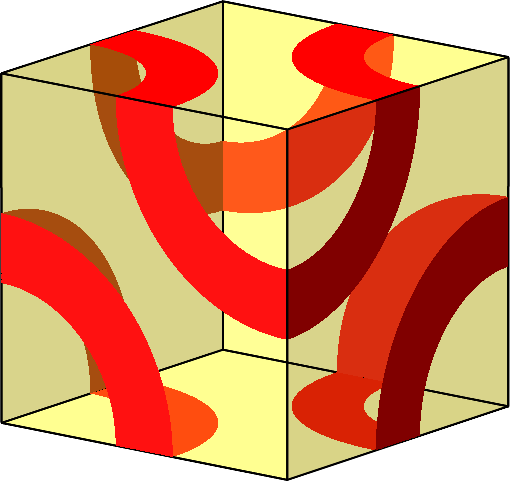
Abb. 10.B: Zwei Dreiecke und ein Sechseck mit bilateraler Symmetrie

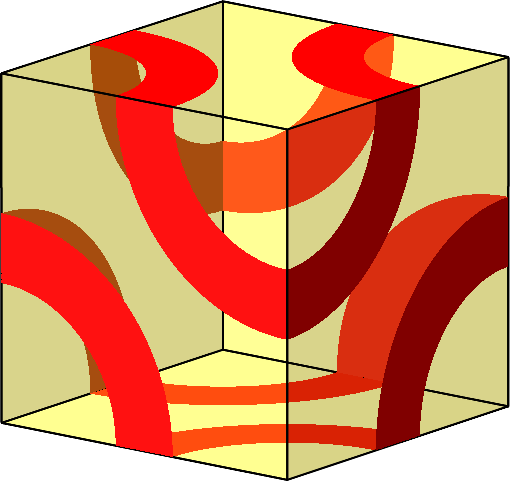
Abb. 10.C: Zwei Sechsecke mit bilateraler Symmetrie

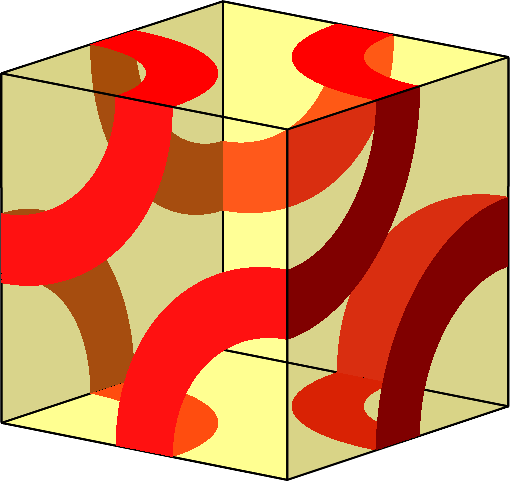
Abb. 10.D: Ein Dreieck und ein Neuneck mit bilateraler Symmetrie

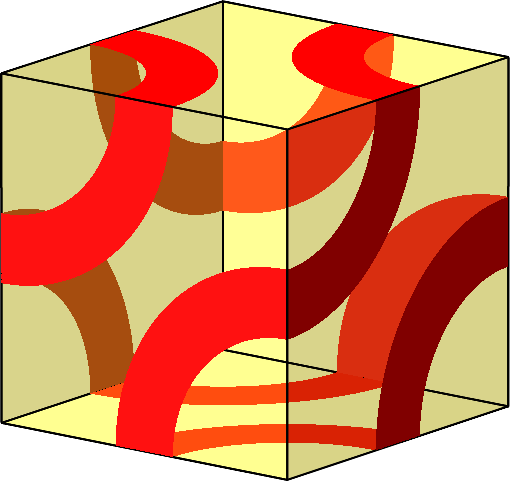
Abb. 10.E: Zwölfeck

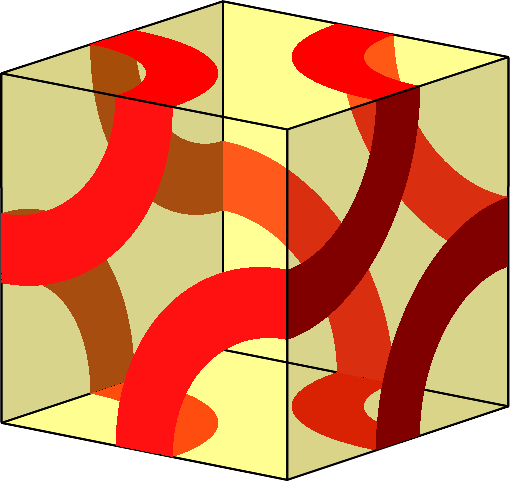
Abb. 10.F: Zwölfeck

Die Zwölfecke der Beispiele E und F sind nach geeigneten Drehungen (von E) spiegelbildlich (Abb. 10.EF).

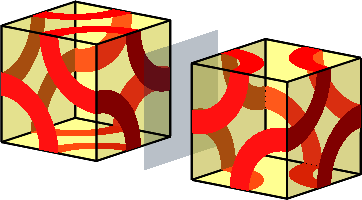
Abb. 10.EF: Spiegelbildliche Zwölfecke

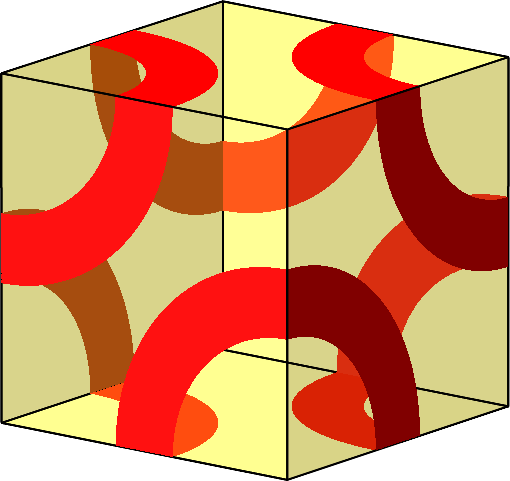
Abb. 10.G: Punktsymmetrisches Zwölfeck

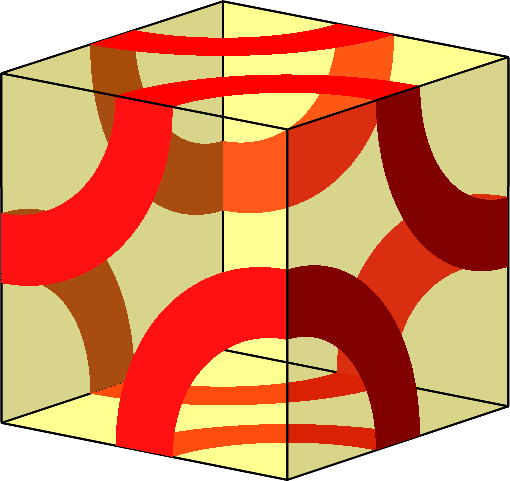
Abb. 10.H: Zwei Dreiecke und ein punktsymmetrisches Sechseck

Weblinks

Hans Walser: Schachbrett

http://www.walser-h-m.ch/hans/Miniaturen/S/Schachbrett2/Schachbrett2.html

Hans Walser: Ulam-Spirale

http://www.walser-h-m.ch/hans/Miniaturen/U/Ulam-Spirale/Ulam-Spirale.html