Hans Walser, [20220125]

Würfelecke

Idee und Anregung: Thomas Jahre, Wochenaufgabe 59-700

1 Problemstellung

Bau einer dreiseitigen Pyramide, eines (unregelmäßigen) Tetraeders also. Die Grundfläche ist ein gelbes gleichseitiges Dreieck. Die drei Seitenflächen sollen zueinander kongruente gleichschenklig rechtwinklige Dreiecke sein.

2 Versuche

2.1 Erster Versuch

Eine Anordnung gemäß Abbildung 1a mit zwei rechten Winkeln an einer Ecke hat zur Folge, dass das dritte Dreieck gleichschenklig sein muss. Also keine Lösung im Sinne der Problemstellung.

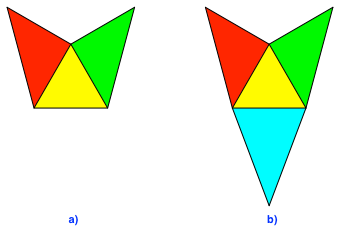
Abb. 1: Zwei rechte Winkel an einer Ecke

Wir erhalten eine schiefe Pyramide (Abb. 2).

Abb. 2: Schiefe Pyramide

Immerhin können wir zwölf solche schiefen Pyramiden lückenlos und überlappungsfrei zu einer geraden Doppel-Sechskantpyramide zusammenfügen (Abb. 3). Diese hat eine Umkugel.

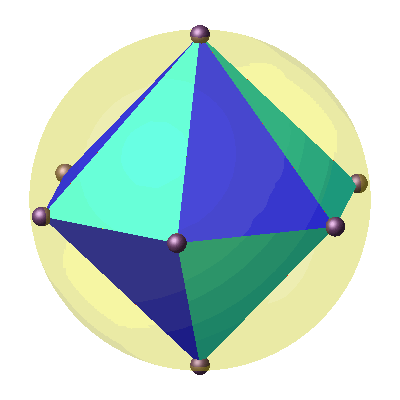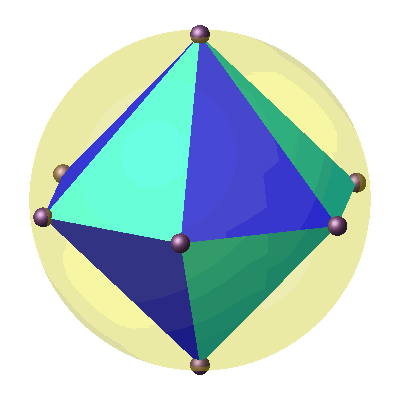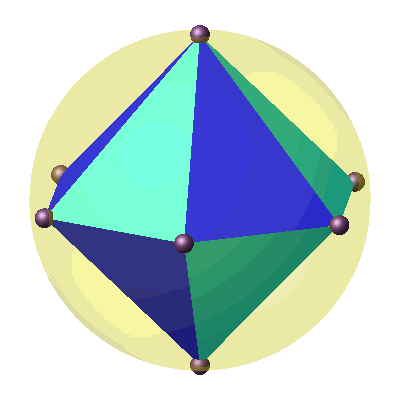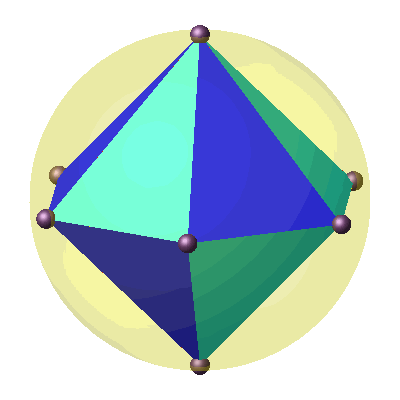
Abb. 3: Dodekaeder

2.2 Zweiter Versuch

Eine Anordnung gemäß Abbildung 4a mit zwei 45°-Winkeln an einer Ecke hat zur Folge, dass das dritte Dreieck gleichseitig sein muss. Also auch keine Lösung im Sinne der Problemstellung.

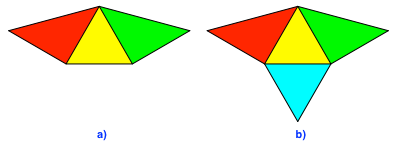
Abb. 4: Zwei 45°-Winkel an einer Ecke

Die Pyramide wird überhängend (Abb.5).

Abb. 5: Überhängende Pyramide

Der Körper kann als Gigampfi (Wippe) dienen (Abb. 6).

Abb. 6: Gigampfi

Die Mittelnormalebene der längsten Kante zerschneidet den Körper in zwei Körper, die Lösungen im Sinne der Problemstellung sind. Wir kommen der Sache näher.

Wir können vier Exemplare unseres Körpers längs der längsten Kante lückenlos und überlappungsfrei zu einem regelmäßigen Oktaeder zusammensetzen (Abb. 7).

Abb. 7: Oktaeder

2.3 Dritter Versuch

In der Anordnung der Abbildung 8a geht es natürlich nicht. Von den Bodenecken gehen ungleich lange Kanten aus, die zusammenkommen müssten. Andererseits hat die Abwicklung eine dreiteilige Drehsymmetrie.

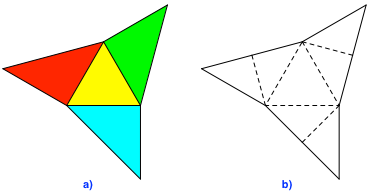
Abb. 8: Geht es noch?

Wenn wir es trotzdem probieren, kommen wir mit den heraufgedrehten Seitenflächen paarweise an den Anschlag (Abb. 9).

Abb. 9: Bis zum Anschlag

Allerdings: Wenn wir am Anschlag innehalten, haben wir genau die Lösung im Sinne der Problemstellung eingekastelt. Wir sind der Sache schon sehr nahe.

Natürlich ist man versucht, das was vorsteht einfach herunterzuklappen (Abb. 10). Wenn man die heruntergeklappten Teile mit Leim fixiert, hat man ein stabiles Modell im Sinne der Problemstellung.

Abb. 10: Herunterklappen

Nun ist der Autor aber ein Fan der Minimallösung. Wenn es ohne geht, macht man es ohne. Ohne Leim.

In der Endposition (Abb. 10) verschwindet der heruntergeklappte rote Teil scheinbar unter der hellblauen Pyramidenwand. Das führt auf folgende Lösungsidee: statt die vorstehenden Teile außen herunterzuklappen und anzuleimen, falten wir sie und stecken sie in die Pyramide hinein (Abb. 11 in zwei Ansichten). Die Abbildung 8b gibt das Schnitt- und Faltmuster dazu. Für das Modell kann gewöhnliches Druckerpapier verwendet werden. Das leimlose Papiermodell ist reversibel. Die Einstecklaschen können wieder herausgezogen werden und das Modell in die Ebene abgewickelt.

Abb. 11: Papiermodell

3 Die Lösung

Werden im Schnittmuster (Abb. 8b) die Einstecklaschen abgeschnitten, ergibt sich die Lösung im Sinne der Problemstellung (Abb.12). Die Symmetrien der Abwicklung sind mit denen der gesuchten Pyramide kompatibel. Natürlich hätten wir schon früher auf diese Lösung kommen sollen, es ist die einzige mit stimmigem Kantenschluss.

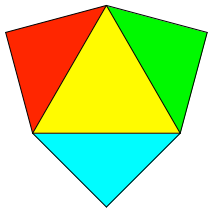
Abb. 12: Die Lösung

Abb. 13: Die Lösung

4 Rechnungen

4.1 Würfelecke

Die Pyramide kann als Würfelecke gesehen werden (Abb. 14).

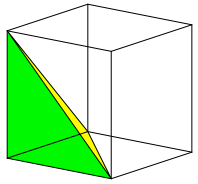
Abb. 14: Würfelecke

Im Einheitswürfel mit der Kantenlänge 1 hat die Würfelecke die Grundfläche ein Halb und daher das Volumen:

4.2 Gleichseitiges Dreieck

Die Endpunkte der drei von einer Würfelecke ausgehenden Kanten spannen ein gleichseitiges Dreieck mit der Seitenlänge sqrt(2) auf (gelb in Abb. 14). Es ist dies das ursprüngliche Bodendreieck der Pyramide (Abb. 12 und 13). Dieses Dreieck hat den Flächeninhalt:

Die drei von der Würfelecke ausgehenden Kanten spannen drei gleichschenklig-rechtwinklige Dreiecke auf. Diese haben je den Flächeninhalt:

Nun gilt folgende interessante Gleichheit:

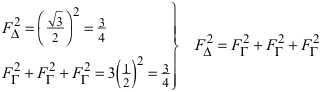
Das erinnert an den Satz von Pythagoras. Dabei werden hier nicht Streckenlängen quadriert, sondern Flächen. Wir operieren in der Dimension vier.

Die Sache hat System.

Das nächste Beispiel: Die Endpunkte der vier von einer Ecke eines 4d-Hyperwürfels ausgehenden Kanten spannen ein regelmäßiges Tetraeder mit der Kantenlänge sqrt(2) auf. Es hat gemäß Formelsammlung das Volumen:

Je drei von der 4d-Hyperürfel-Ecke ausgehende Kanten spannen eine Pyramide der Abbildung 14 auf. Da wir insgesamt vier ausgehende Kanten haben, ergeben sich vier solche Pyramiden. Sie haben je das Volumen:

Wir ahnen, was kommt:

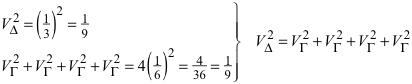
Nun werden Volumina quadriert, wir arbeiten also in der Dimension 6.

Man kann (induktiv) zeigen, dass Entsprechendes auch für höherdimensionale reguläre Simplexe gilt.

Websites

Thomas Jahre: Wochenaufgabe

https://www.schulmodell.eu/unterricht/faecher/mathematik/wochenaufgabe.html

Hans Walser: Simplex

http://www.walser-h-m.ch/hans/Miniaturen/S/Simplex/Simplex.htm

Hans Walser: Würfelecke und Davidstern

http://www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelecke/Wuerfelecke.htm