Hans Walser, [20221105]
Verhältnisinvarianz
Idee und Anregung: Stanley Rabinowitz, Maik Rentsch
1 Worum geht es?
Invariantes Längenverhältnis bei zwei sich berührenden Kreisen
2 Sehne und Tangente
Wir beginnen mit zwei sich berührenden Kreisen (Abb. 1). Auf dem einen (blauen) Kreis wählen wir einen beliebigen Punkt und zeichnen die (grüne) Sehne zum Berührungspunkt der beiden Kreise. Weiter zeichnen wir die (violetten) Tangentenabschnitte von diesem gewählten Punkt aus an den zweiten (roten) Kreis.

Abb. 1: Basisfigur
Dann gilt (Theorem von Stanley Rabinowitz): Das Längenverhältnis Tangentenabschnitt zu Sehne bleibt invariant, wenn der gewählte Punkt auf dem blauen Kreis zirkuliert (Abb. 2).
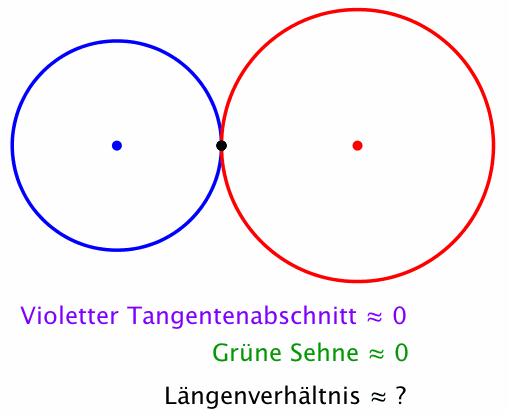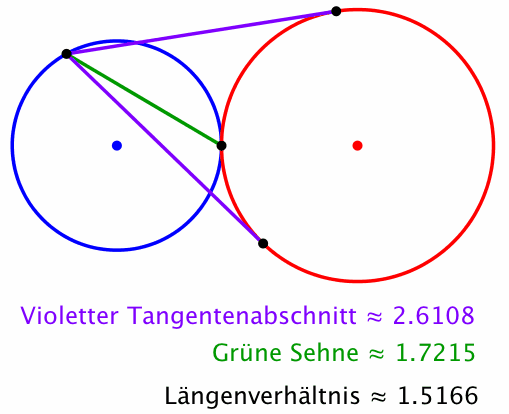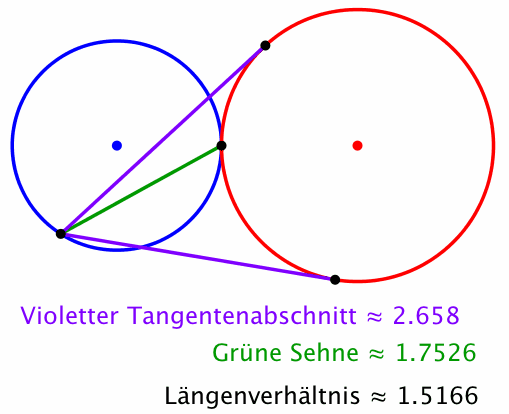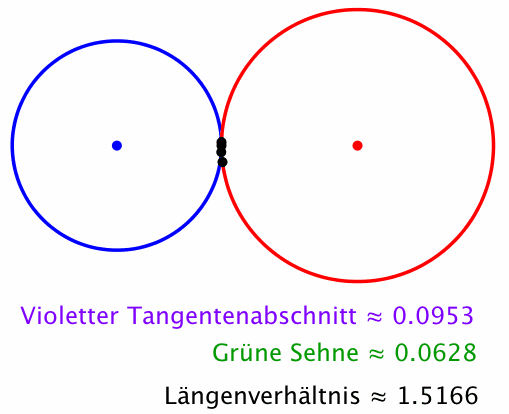
Abb. 2: Invariantes Längenverhältnis
3 Beweis
Rechnerischer Beweis mit den Bezeichnungen der Abbildung 3.
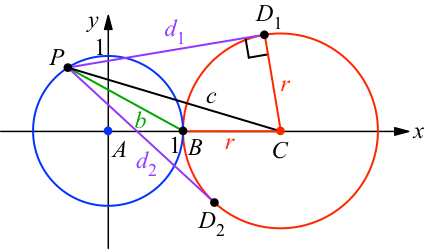
Abb. 3: Maße und Bezeichnungen
Der blaue Kreis habe den Mittelpunkt A im Ursprung den Radius 1, der rote Kreis den Mittelpunkt C und den Radius r.
Der Berührungspunkt B hat die Koordinaten:
![]()
Der Mittelpunkt C des roten Kreises hat die Koordinaten:
![]()
Für den Punkt P auf dem blauen Kreis verwenden wir die Schreibweise:
![]()
Aus Symmetriegründen können wir uns auf die Punkte P im ersten und zweiten Quadranten des Koordinatensystems (also mit y ≥ 0) beschränken.
Für die grüne Sehne b erhalten wir mit Pythagoras:
![]()
Für die Strecke c ergibt sich ebenfalls mit Pythagoras:
![]()
Für den Tangentenabschnitt d1 erhalten wir wiederum mit Pythagoras:
![]()
Der zweite Tangentenabschnitt d2 ist gleich lang.
Für das gesuchte Längenverhältnis ergibt sich:
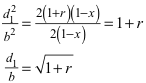
Diese Längenverhältnis hängt nur vom Radius r des roten Kreises ab, ist aber unabhängig von x und damit unabhängig von der Lage von P auf dem blauen Kreis. Dies war zu zeigen.
Im Beispiel der Abbildungen 1 und 3 ist r = 1.3. Daher erhalten wir für das Längenverhältnis:
![]()
4 Spezielle Beispiele
Wir diskutieren einige Beispiele bezüglich des Radius‘ r des roten Kreises. Dabei können wir einerseits das Längenverhältnis mit der Formel
![]()
berechnen. Andererseits können wir aber auch, nachdem die Verhältnisinvarianz gemäß dem Theorem von Rabinowitz etabliert ist, dieses Verhältnis in einem geeigneten geometrischen Sonderfall ablesen.
4.1 Zwei gleich große Kreise
Das Längenverhältnis ist die Quadratwurzel aus 2 (Abb. 4). Dies ist auch das Seitenverhältnis im DIN-Format.
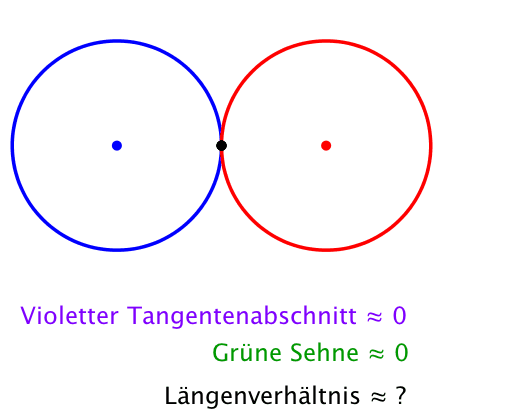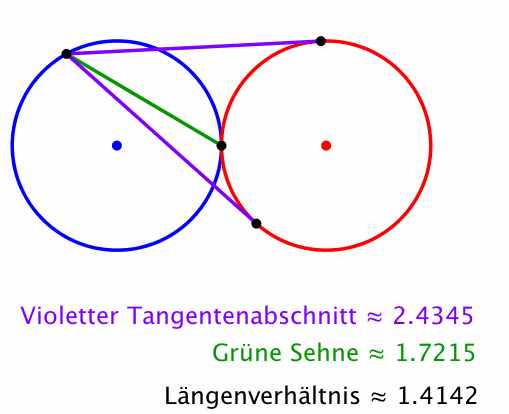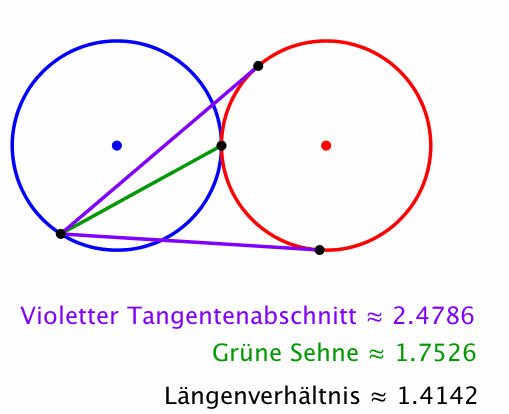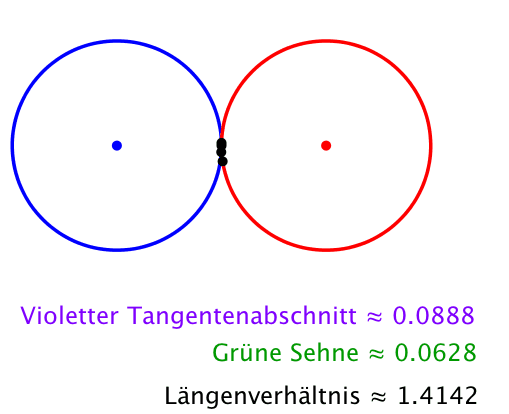
Abb. 4: Zwei gleich große Kreise
Das Längenverhältnis kann im Sonderfall eines rechtwinklig-gleichschenkligen Dreiecks (Abb. 5) sofort eingesehen werden.

Abb. 5: Sonderfall
4.2 Goldener Schnitt
Wir setzen:
Dies ist der Goldene Schnitt. Der Radius r des roten Kreises ist der Major, der Radius 1 des blauen Kreise der Minor.
In diesem Fall ist auch das Längenverhältnis im Goldenen Schnitt. Der violette Tangentenabschnitt ist der Major, die grüne Sehne der Minor.
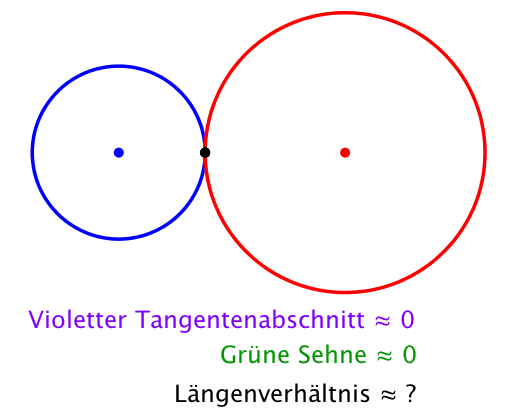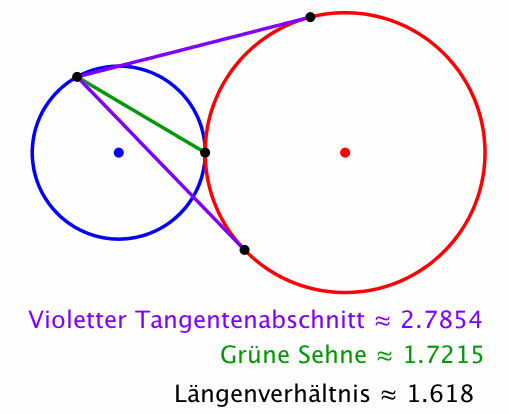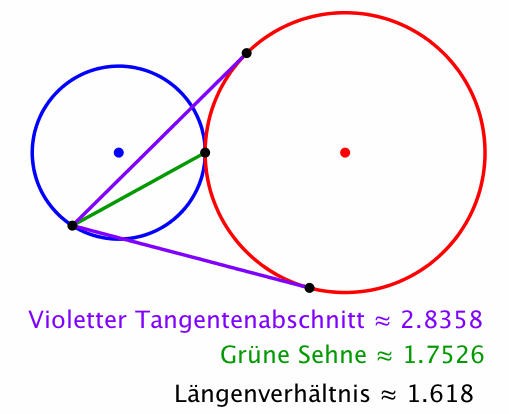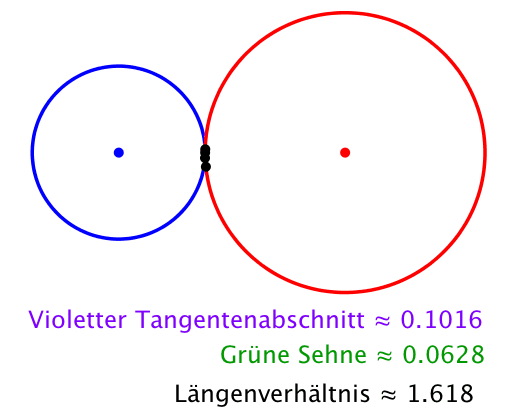
Abb. 6: Goldener Schnitt
Im Sonderfall (Abb. 7) erkennen wir eine klassische Konstruktion des Goldenen Schnittes.
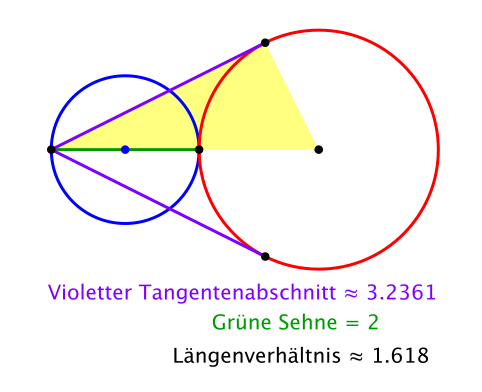
Abb. 7: Konstruktion des Goldenen Schnittes
4.3 Roter Kreis doppelt so groß wie der blaue
Wir setzen r = 2 (Abb. 8). Für das Längenverhältnis erhalten wir die Quadratwurzel aus 3.
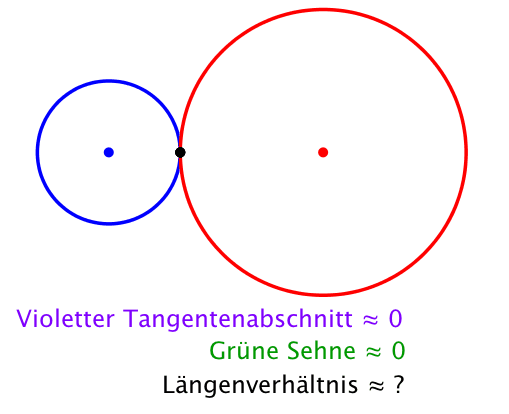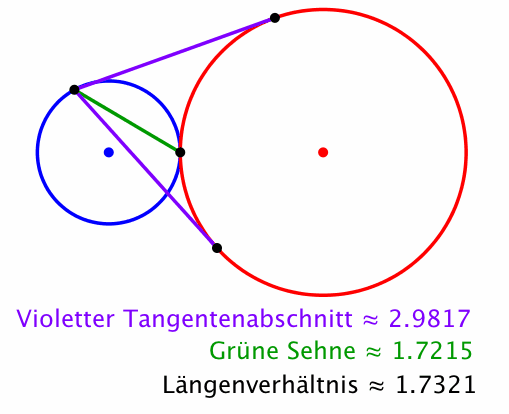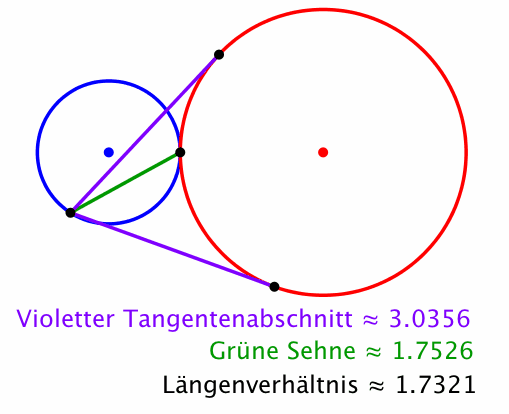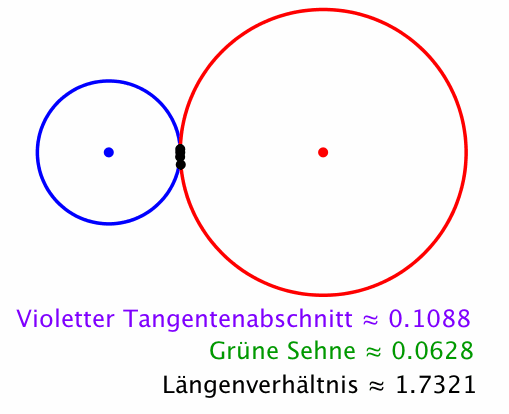
Abb. 8: Quadratwurzel aus 3
Im Sonderfall (Abb. 9) ergibt sich ein gleichseitiges Dreieck.
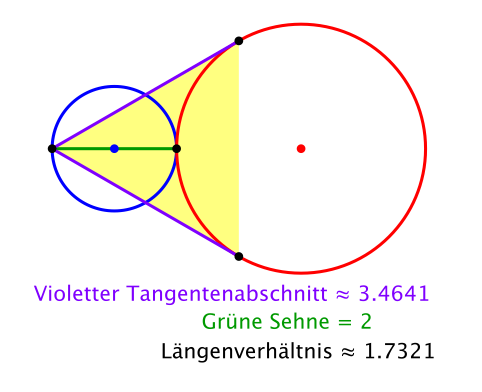
Abb. 9: Gleichseitiges Dreieck
Weblinks
Stanley Rabinowitz
Hans Walser: Goldener Schnitt
http://www.walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_5/Goldener_Schnitt_5.html
Hans Walser: Goldener Schnitt
http://www.walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_6/Goldener_Schnitt_6.html
Literatur
Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.