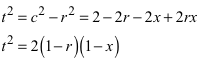Hans Walser, [20221104]
Goldener Schnitt
Anregung: Maik Rentsch
1 Worum geht es?
Im Kontext eines Invariantentheorems („Pfeiltheorem“) erscheint der Goldene Schnitt.
2 Das Pfeiltheorem
Wir zeichnen zwei Kreise, die sich von innen berühren (Abb. 1). Auf dem äußeren (roten) Kreis wählen wir einen beliebigen Punkt und zeichnen von diesem Punkt aus einerseits die Tangentenabschnitte (violett) zum inneren (blauen) Kreis und andererseits die Sehne zum Berührungspunkt der beiden Kreise. Diese Sehne schneidet aus dem inneren Kreis eine kleinere Sehne (grün) heraus.
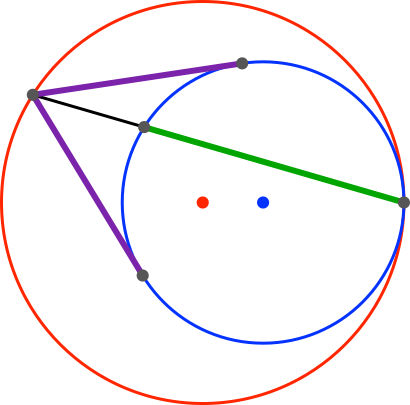
Abb. 1: Pfeil
Das Pfeiltheorem besagt nun, dass das Längenverhältnis der grünen Sehne zu einem violetten Tangentenabschnitt invariant bleibt, wenn der Punkt auf dem roten Kreis zirkuliert (Abb. 2, die Maßeinheit ist der Radius des roten Kreises).
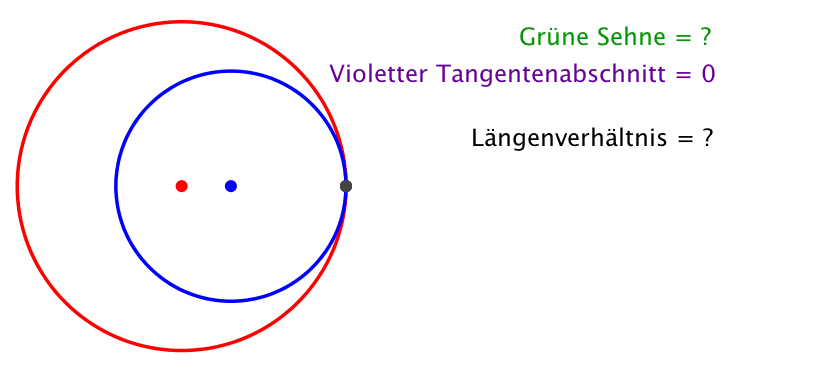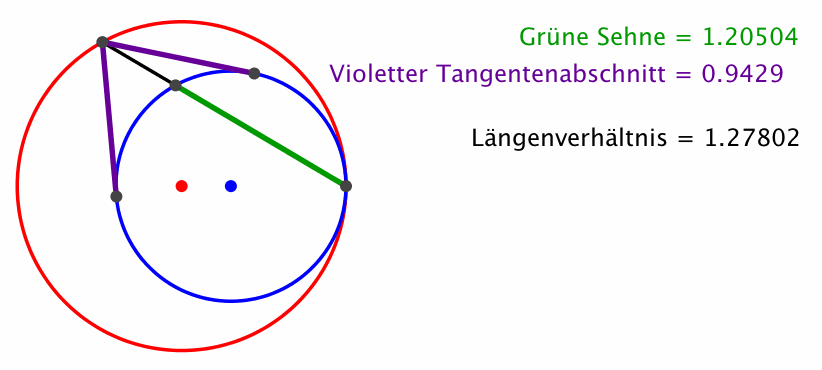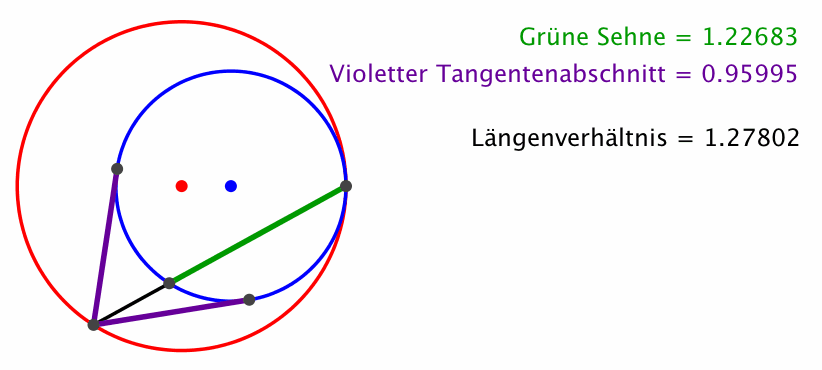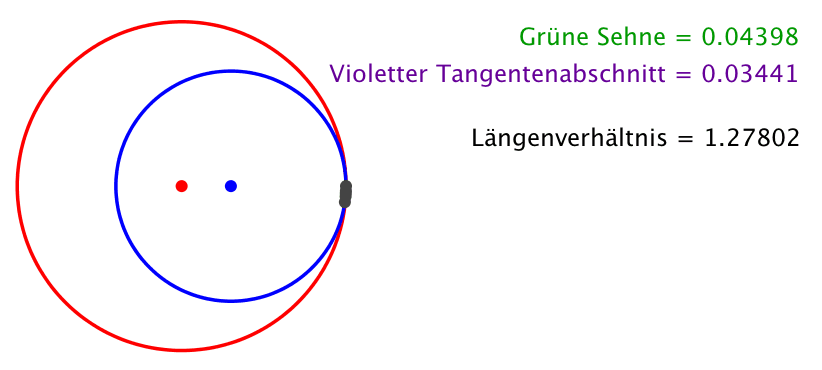
Abb. 2: Invariantes Längenverhältnis
3 Beweise
3.1 Stanley Rabinowitz
Die Invarianz des Längenverhältnisses kann aus einem Theorem von Stanley Rabinowitz gefolgert werden. Dabei wird die Perspektivähnlichkeit der beiden Kreise verwendet.
3.2 Rechnerischer Beweis
Für einen rechnerischen Beweis arbeiten wir mit den Bezeichnungen der Abbildung 3. Der äußere (rote) Kreis ist der Einheitskreis mit dem Zentrum im Ursprung. Der innere (blaue) Kreis hat das Zentrum C und den Radius r.
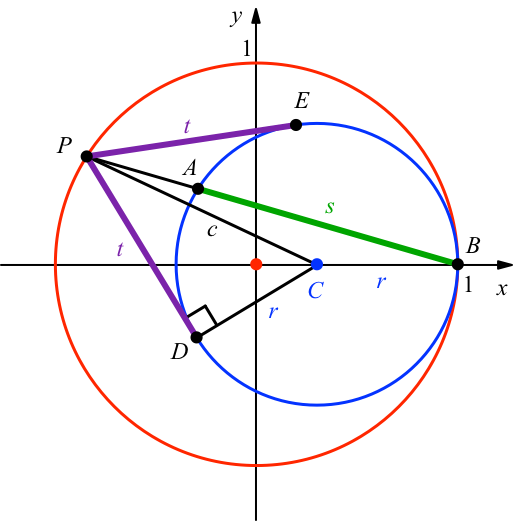
Abb. 3: Bezeichnungen
Aus Symmetriegründen können wir uns auf die obere Hälfte (P in den Quadraten mit y ≥ 0) beschränken.
Den Punkt P bezeichnen wir mit kartesischen Koordinaten:
![]()
Wir verwenden x als Parameter des Problems.
Für die grüne Sehnenlänge s erhalten wir:
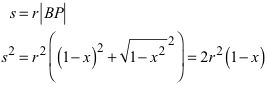
Weiter ist:
![]()
Und schließlich:
Für das gesuchte Verhältnis ergibt sich:
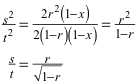
Dieses Längenverhältnis hängt nur von r ab, dem Radius des inneren (blauen) Kreises. Es ist unabhängig von x und damit von der Position des Punktes P auf dem äußeren (roten) Kreis. Dies war zu beweisen.
4 Verhältnis 1:1
Für welchen Radius r des inneren (blauen) Kreises erhalten wir das Längenverhältnis 1:1? Die grüne Sehne soll also gleich lang sein wie ein violetter Tangentenabschnitt.
Wir haben die Bedingung:
![]()
Die Bedingung führt auf die quadratische Gleichung:
![]()
Die positive Lösung dieser quadratischen Gleichung ist:
![]()
Dies ist der Kehrwert des Goldenen Schnittes:
![]()
Die Kreisradien sind nun im Verhältnis des Goldenen Schnittes (Abb. 4).
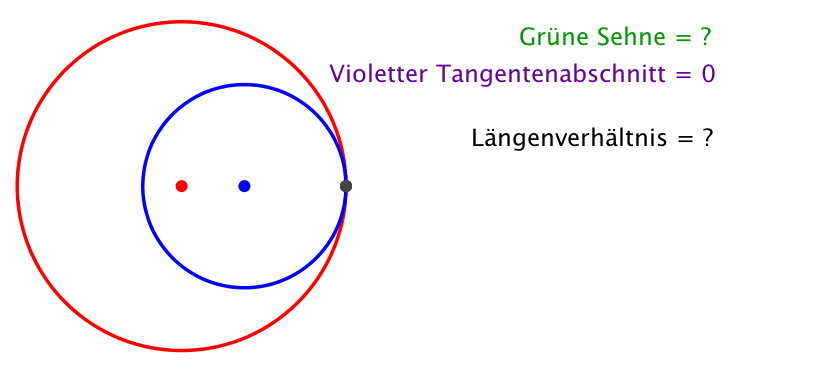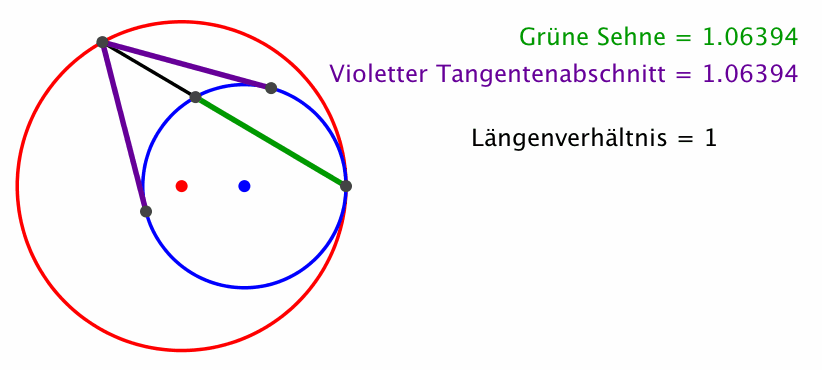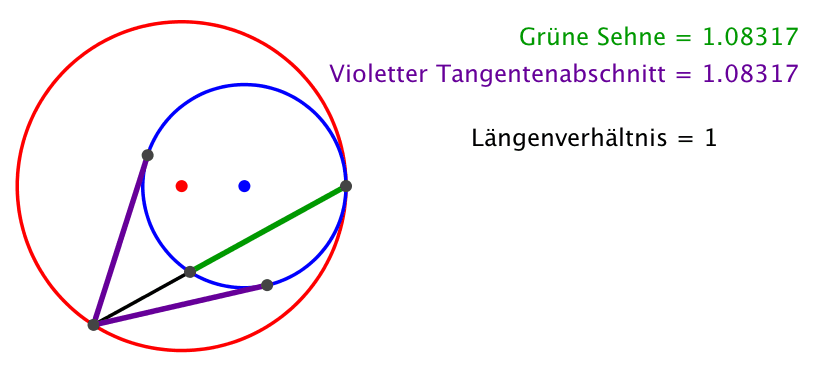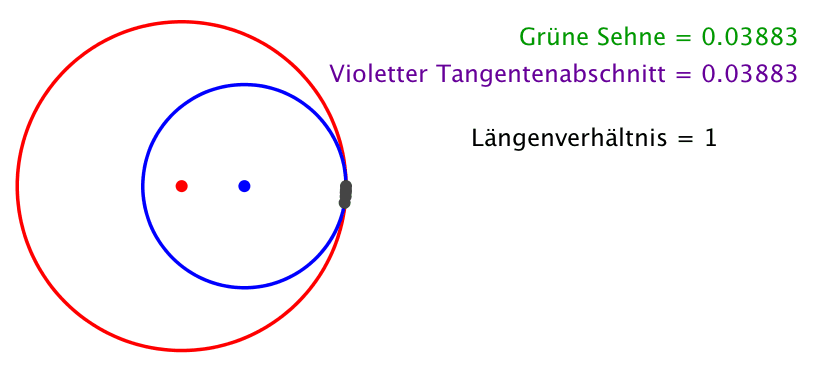
Abb. 4: Kreisradien im Goldenen Schnitt
Weblinks
Stanley Rabinowitz
Hans Walser: Goldener Schnitt
http://www.walser-h-m.ch/hans/Miniaturen/G/Goldener_Schnitt_5/Goldener_Schnitt_5.html
Literatur
Walser, Hans (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.