1 Worum es geht

Schönheit enthält Unschönheit, Unschönheit enthält Schönheit. Ein klassisches Dilemma.

2 Die kanonische Kreisfigur

Die Abbildung 1 zeigt die kanonische Kreisfigur. Sie besteht aus sieben kongruenten Kreisen. Die eingezeichneten Punkte sind die Kreiszentren.

Abb. 1: Kanonische Kreisfigur

Die kanonische Kreisfigur gilt als „schön“. Sie hat die Symmetriegruppe des regelmäßigen Sechsecks.

Sie ist auch Konstruktionsbasis anderer schöner Figuren, etwa der Blüte der Abbildung 2, welche allerdings keine Symmetrieachsen hat. Zum Zeichnen wegen der zyklischen Hackordnung der Blütenblätter leicht tricky.

Abb. 2: Blume

Zurück zur kanonischen Kreisfigur (Abb. 1). Sechs der sieben Kreise enthalten drei Kreiszentren, der siebte aber deren sechse. Sechs der Zentren sind Schnittpunkte von je drei Kreisen, das siebte aber Schnittpunkt von sechs Kreisen. Diese Ausnahme-Situation eines Kreises und eines Punktes ist unschön. Die Topologie der Inzidenzen ist ungleichmäßig.

So viel zur Unschönheit in der Schönheit.

3 Eine andere Kreisfigur

Die Abbildung 3 gibt eine Kreisfigur mit nun acht Kreisen. Diese Figur hat viel weniger Symmetrien als die kanonische Kreisfigur, sie hat nur noch die Symmetriegruppe des Rechteckes.

Abb. 3: Acht Kreise

Jedoch: alle acht Kreise enthalten nun genau drei Kreiszentren, und jedes Kreiszentrum ist Schnittpunkt von genau drei Kreisen. Die Inzidenztopologie ist regelmäßig.

So viel zur Schönheit in der Unschönheit.

Die Kreisfigur der Abbildung 3 gestattet Veränderungen, zum Beispiel die Kreisbewegung der Abbildung 4. Dabei bleibt die Inzidenztopologie invariant. Hingegen hat die Figur im Allgemeinen nur noch die Symmetriegruppe des Parallelogramms. Sie ist lediglich noch punktsymmetrisch.

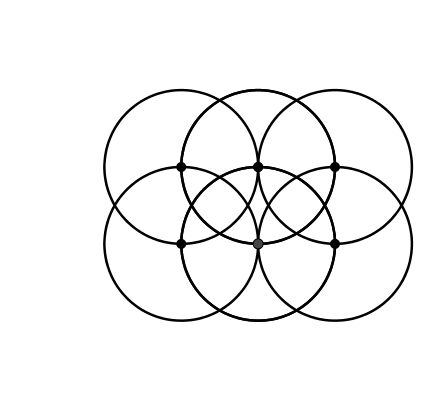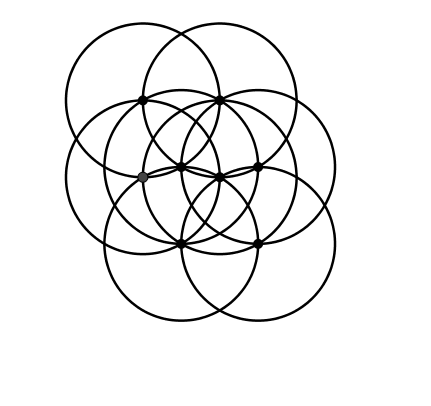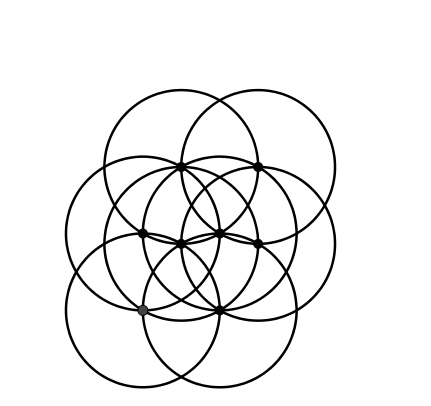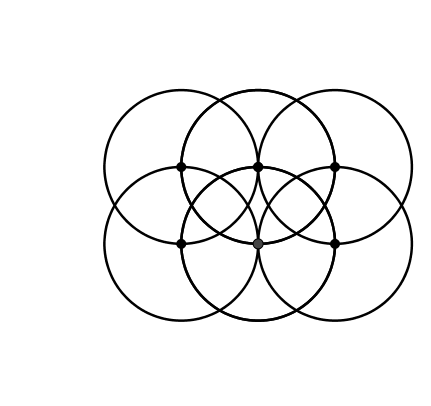
Abb. 4: Veränderung

4 Schönheit und Schönheit

Nun also das Problem: Gibt es eine Kreisfigur mit hoher Symmetrie und gleichzeitig regelmäßiger Inzidenztopologie?

Die Abbildung 5 zeigt eine Lösung.

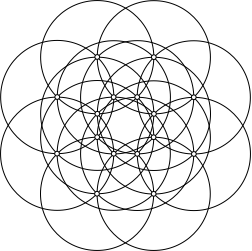
Abb. 5: Eine Lösung

Wir haben 16 Kreise. Die Kreisfigur hat die Symmetriegruppe des regelmäßigen Achteckes. Jeder Kreis enthält vier Kreiszentren, und jedes Kreiszentrum ist Schnittpunkt von genau vier Kreisen.

5 Hintergrund

Wir zeichnen alle Strecken der Länge des Kreisradius‘ ein. Für die kanonische Kreisfigur (Abb. 1) erhalten wir ein regelmäßiges Sechseck mit Mittelpunktdiagonalen (Abb. 6).

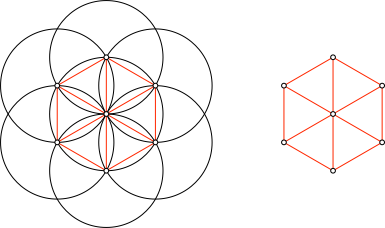
Abb. 6: Sechseck

Aus der Figur der Abbildung 3 ergibt sich eine Würfeldarstellung (Abb. 7 und 8).

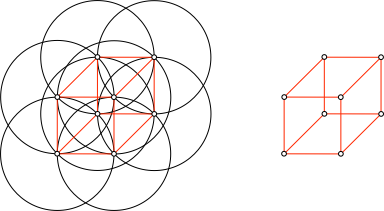
Abb. 7: Würfeldarstellung

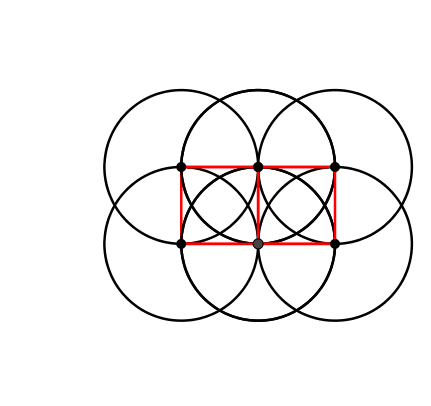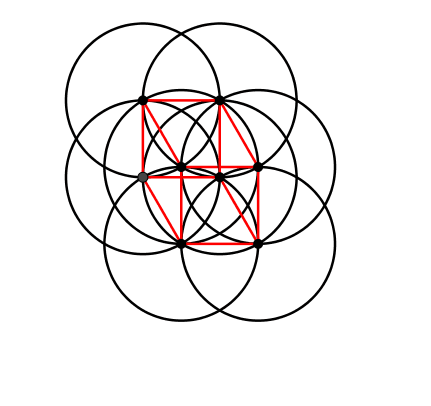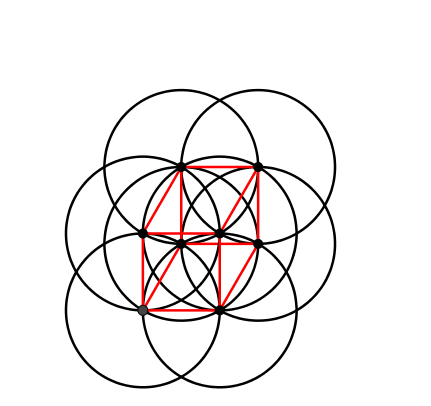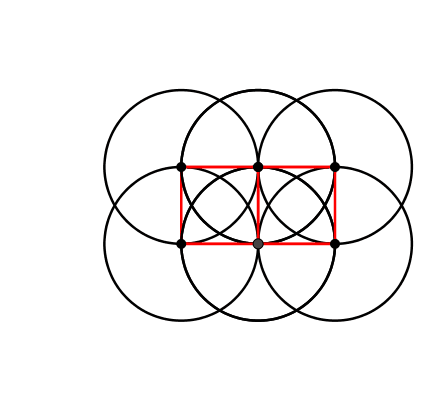
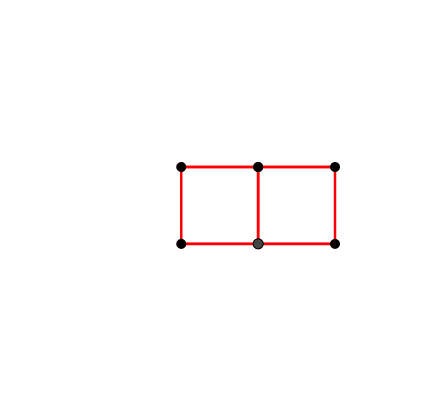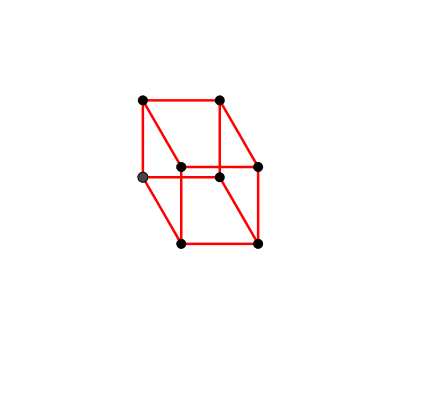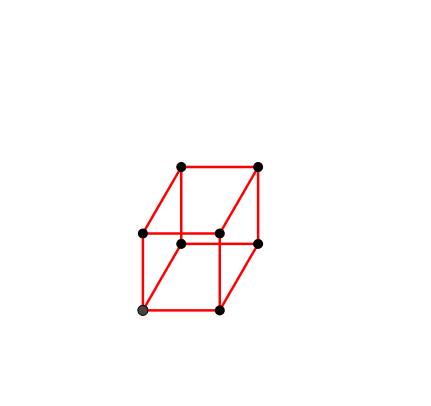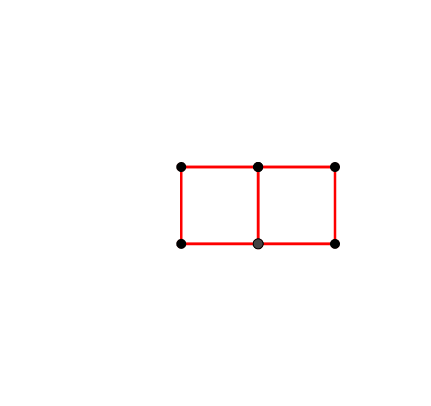
Ein Bild, das Reihe, Diagramm, Design enthält.

Automatisch generierte Beschreibung

Abb. 8: Kinematischer Würfel

Hinterher ist man immer klüger: das Sechseck aus der kanonischen Kreisfigur (Abb. 6) ist natürlich auch eine Würfeldarstellung, aber eine spezielle. Wir sehen den Würfel über eine Raumdiagonale. Der Punkt in der Mitte ist das Bild von zwei verschiedenen Punkten, zählt also doppelt. Daher die (scheinbaren) Unregelmäßigkeiten in der topologischen Inzidenzstruktur.

Aus der Lösung der Abbildung 5 ergibt sich eine Darstellung eines vierdimensionalen Hyperwürfels (Abb. 9).

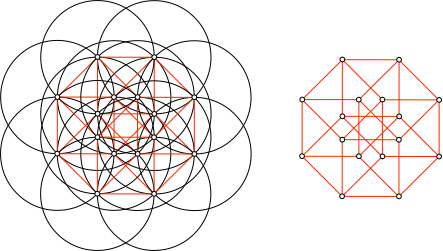
Abb. 9: Vierdimensionaler Hyperwürfel

6 Ausblick

Es gibt eine noch viel einfachere schön-schöne Lösung (Tipp: Dimension 2).

In welchen Dimensionen gibt es Lösungen?

Weblinks

Hans Walser: Hyperwürfel

http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel4/Hyperwuerfel4.html