Hans Walser, [20220908]
Hyperwürfel
1 Worum geht es?
Verschiede Darstellungsarten der Entstehung von Hyperwürfeln.
Die Kantenlänge ist jeweils 1.
2 Echt
Der nulldimensionale Hyperwürfel ist der Punkt.
2.1 Strecke
Der eindimensionale Hyperwürfel ist die Strecke. Man kann sie als Spur eines gradlinig bewegten Punktes sehen (Abb. 1).

![]()
Abb. 1: Strecke
2.2 Quadrat
Wird eine Strecke senkrecht zu ihrer Richtung bewegt, entsteht ein Quadrat (Abb. 2). Dies ist der zweidimensionale Hyperwürfel.


Abb. 2: Quadrat
3 Würfel
Ab jetzt wird geschummelt.
3.1 Allgemein
Der Würfel (Abb. 3) sieht recht echt aus. Allerdings sehen wir nur ein zweidimensionales Bild einer an sich dreidimensionalen Figur.

Abb. 3: Würfel
In der Abbildung 4 werden zusätzlich Inkreis und Inkugel ins Spiel gebracht.

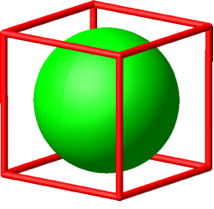
Abb. 4: Inkreis und Inkugel
3.2 Zentriert
In der Abbildung 5 ist das Bild mit den drei räumlichen Einheitsvektoren so angeordnet, dass planimetrisch eine Sternfigur mit dem Ursprung im Zentrum gesehen werden kann. Wegen der Beleuchtung sehen wir die Regelmäßigkeit etwas gestört.
Diese spezielle Sicht wird als isometrische Darstellung bezeichnet.
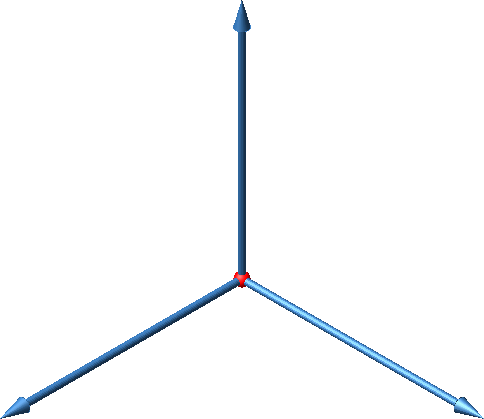
Abb. 5: Sternfigur. Isometrische Darstellung
Die Abbildung 6 zeigt die zugehörige Würfelfigur. Wir sehen ein regelmäßiges Sechseck. Von den acht Eckpunkten des Würfels fallen in der Abbildung zwei aufeinander, nämlich die beiden in der Mitte der planimetrischen Figur.
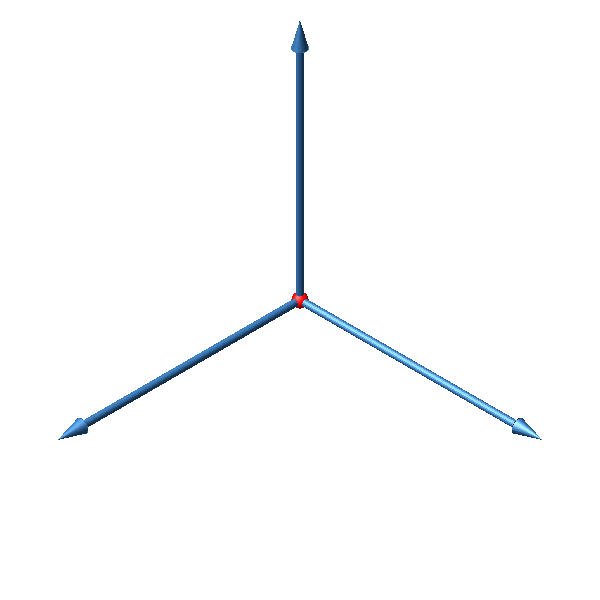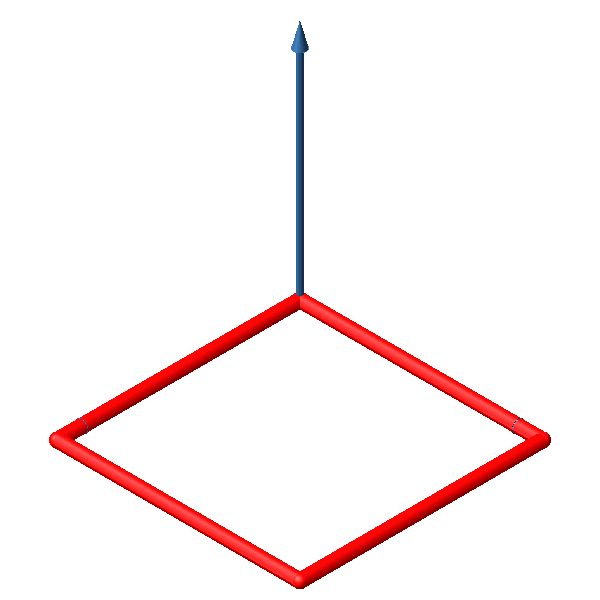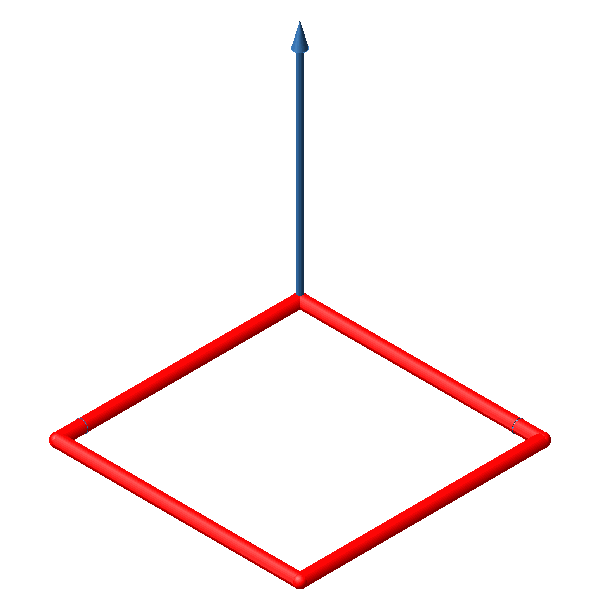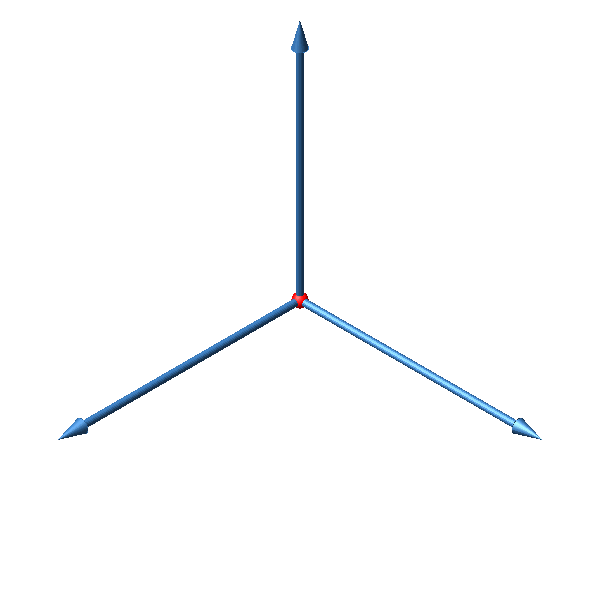
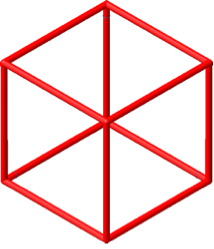
Abb. 6: Würfel in isometrischer Darstellung
3.3 Fächer
In der Abbildung 7 sind die drei räumlichen Einheitsvektoren scheinbar fächerförmig angeordnet.
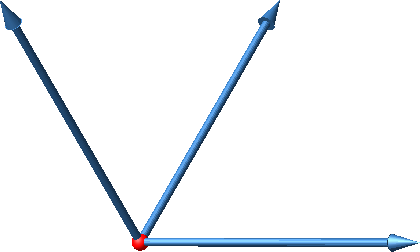
Abb. 7: Fächer
Die Abbildung 8 zeigt die zugehörige Würfelfigur. Sie erscheint ebenfalls als regelmäßiges Sechseck. Es handelt sich ebenfalls um eine isometrische Darstellung.

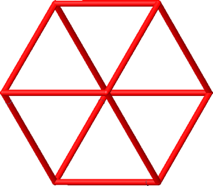
Abb. 8: Andere isometrische Darstellung
Die beiden Darstellungen (Abb. 6 und Abb. 8) unterscheiden sich im Startpunkt, haben aber (fast) dieselbe Endfigur. Mit scharfem Auge sieht man einen Unterschied im Mittelpunkt.
4 Verschiedene Dimensionen
Wir übertragen die Sternfigur und die Fächerdarstellung auf verschiedene Dimensionen n. Die Darstellung ist jeweils rein zweidimensional. Anstelle der drei räumlichen Einheitsvektoren arbeiten wir mit n beliebig wählbaren Vektoren.
Der erste Vektor wird jeweils horizontal nach rechts gezeichnet.
4.1 Strecke
Die Stern-Lösung (Abb. 9) und die Fächer-Lösung (Abb. 10) unterscheiden sich nicht.
![]()
![]()
Abb. 9: Stern-Lösung
![]()
![]()
Abb. 10: Fächer-Lösung
4.2 Quadrat
Beim Quadrat sieht die Stern-Lösung (Abb. 11) merkwürdig aus.
![]()
![]()
Abb. 11: Stern-Lösung
Bei der Fächer-Lösung (Abb. 12) sehen wir ein echtes Quadrat.


Abb. 12: Quadrat bei der Fächer-Lösung
Die merkwürdige Figur der Abbildung 11 bedarf einer Erklärung. So sieht eine Bewohnerin einer zweidimensionalen Welt ein Quadrat, wenn sie dieses über eine Ecke ansieht gemäß Abbildung 13. Vorstellung: Auf einem See ist mit vier Bojen ein Quadrat markiert. Eine Schwimmerin nähert sich der Figur.
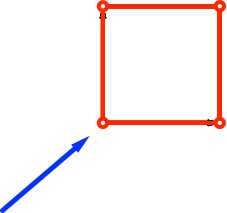
Abb. 13: Sicht über die Quadratecke
Der mittlere Punkt der Endfigur der Abbildung 11 ist doppelt zu zählen (Abb. 14). Aus der Sicht der zweidimensionalen Welt liegen zwei diametrale Eckpunkte des Quadrates hintereinander. Die Zahlenfolge 1 , 2, 1 erinnert an die zweite Zeile im Pascalschen Dreieck der Binomialkoeffizienten.
![]()
Abb. 14: In der Mitte zwei Punkte hintereinander
4.3 Würfel
Die Abbildung 15 entspricht der Abbildung 6 in modifizierter Darstellung.
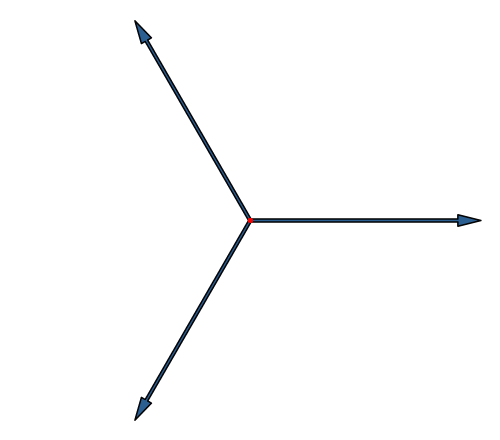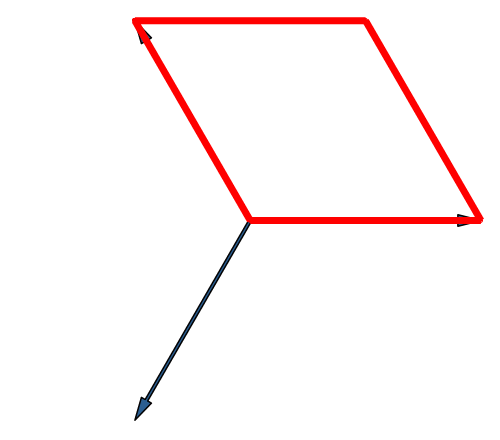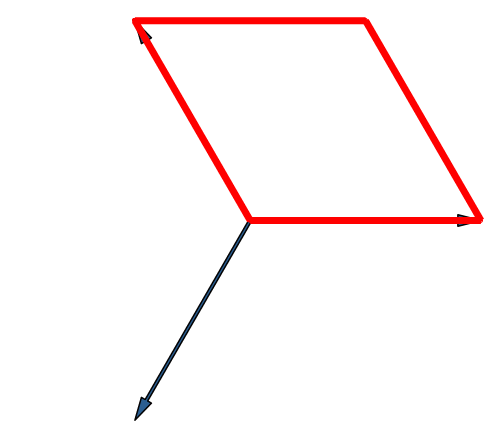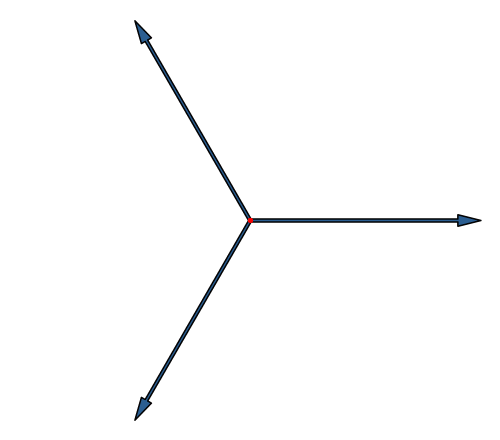
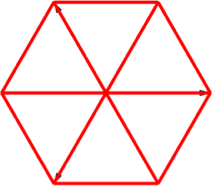
Abb. 15: Würfel in Stern-Lösung
Die Abbildung 16 entspricht der Abbildung 8 in modifizierter Darstellung.
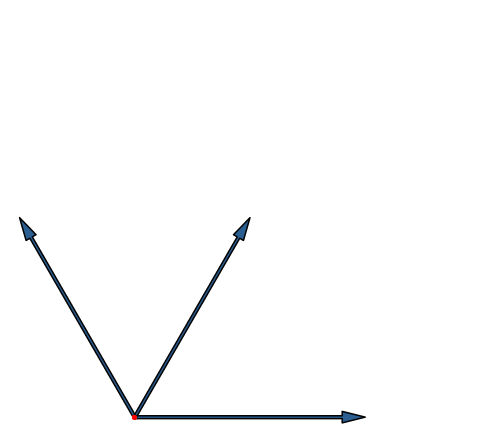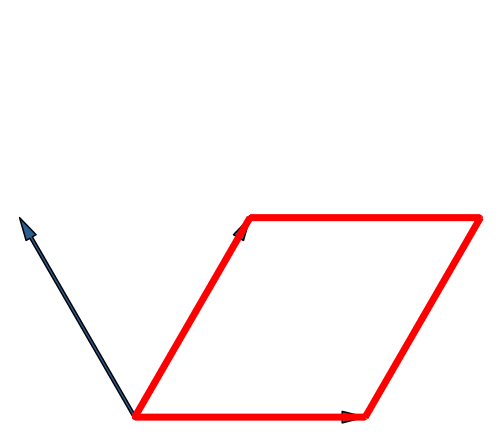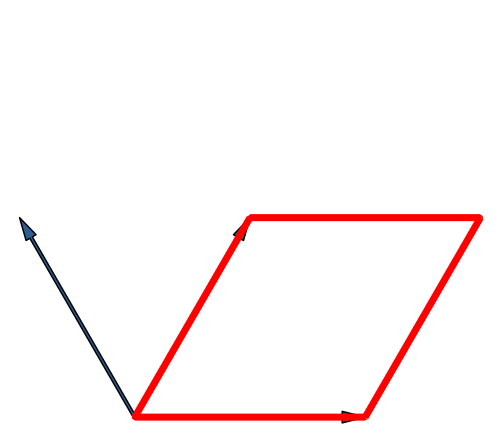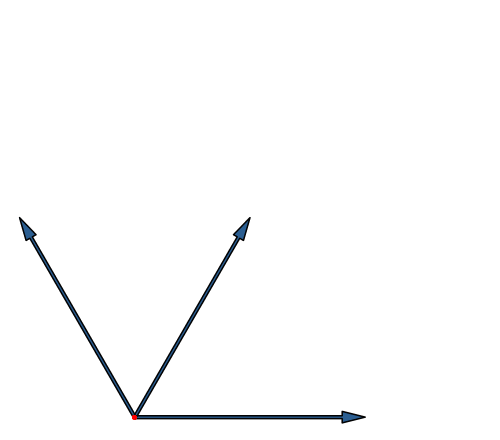
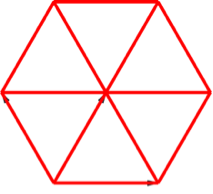
Abb. 16: Würfel in Fächer-Lösung
4.4 Vierdimensionaler Hyperwürfel
Und nun endlich der Sprung in höhere Dimensionen.
Die Abbildung 17 zeigt die Stern-Lösung für den vierdimensionalen Hyperwürfel. Die Endfigur ist ein Quadratgitter.
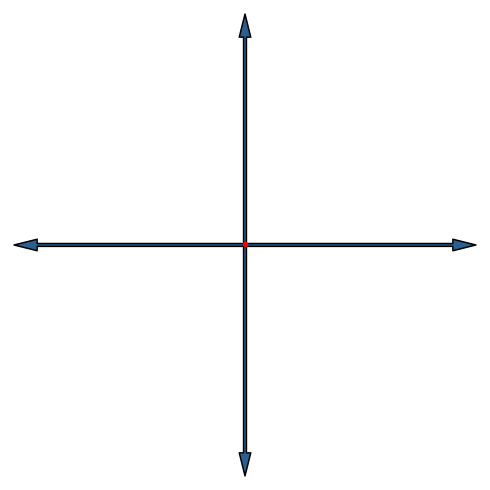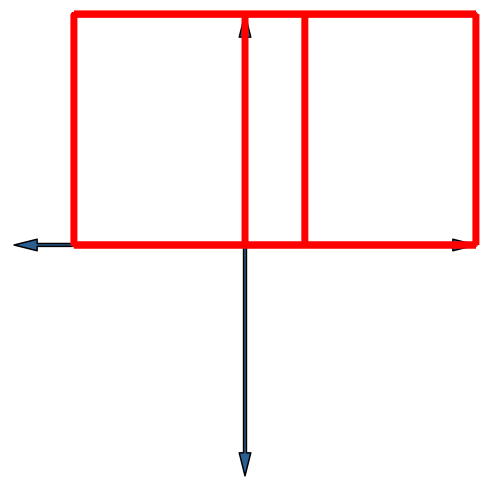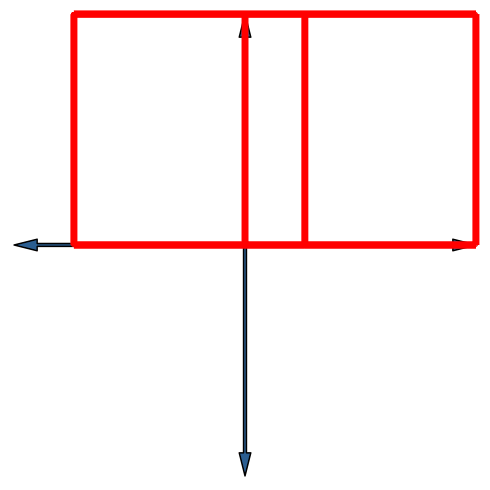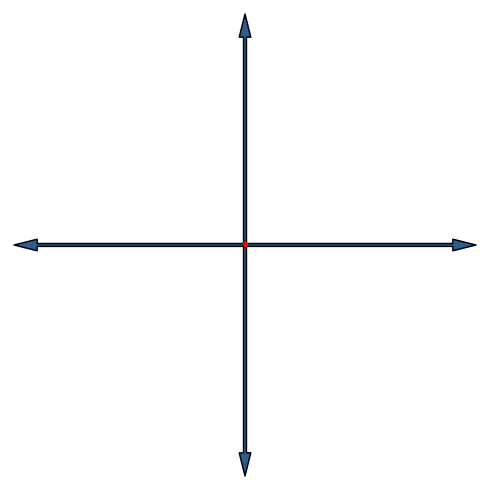
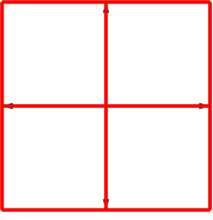
Abb. 17: Vierdimensionaler Hyperwürfel in Stern-Lösung
Der vierdimensionale Hyperwürfel hat 24 = 16 Eckpunkte. Die Abbildung 18 zeigt deren Vielfachheit in der Stern-Lösung.
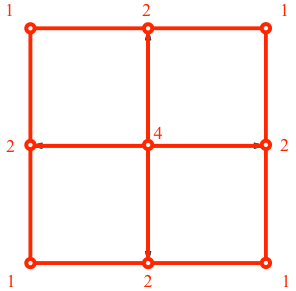
Abb. 18: Eckenzahlen
Die Abbildung 19 gibt die Fächer-Lösung. Der Umriss der Endfigur ist ein regelmäßiges Achteck. Wir sehen jeden der 16 Eckpunkte einzeln. In der Mitte der Figur ist ein Loch, also kein Eckpunkt des Hyperwürfels.
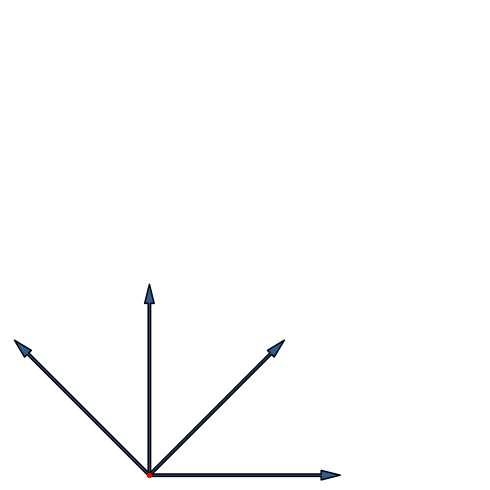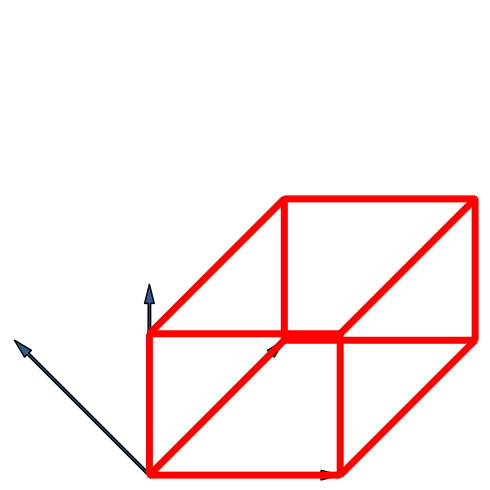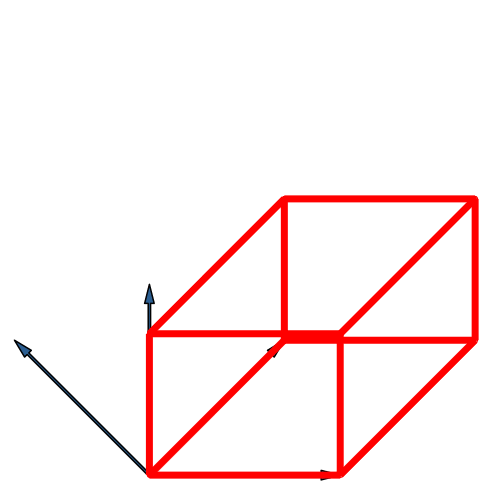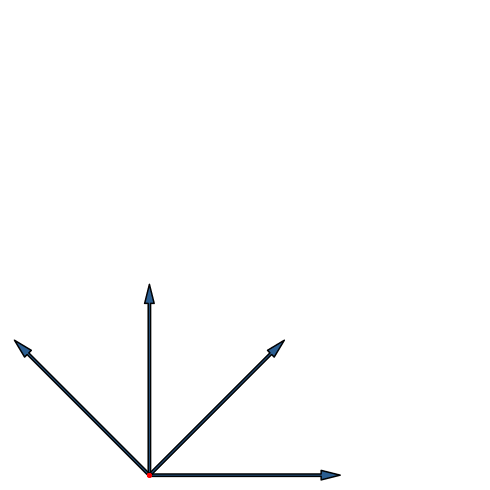
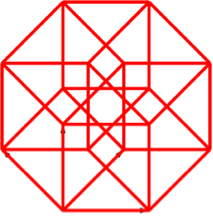
Abb. 19: Vierdimensionaler Hyperwürfel in Fächer-Lösung
4.5 Fünfdimensionaler Hyperwürfel
Die Abbildung 20 zeigt die Stern-Lösung, die Abbildung 21 die Fächer-Lösung. Wir sehen in der Endfigur keinen Unterschied.
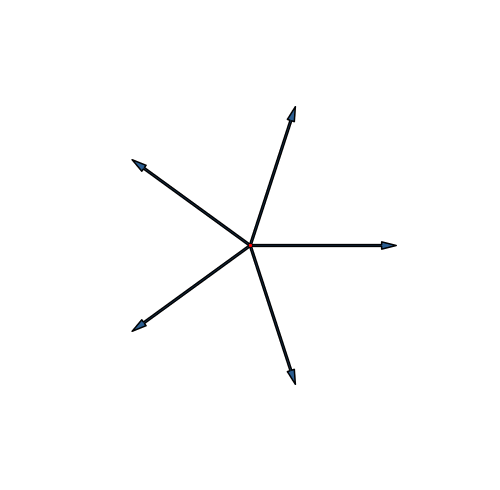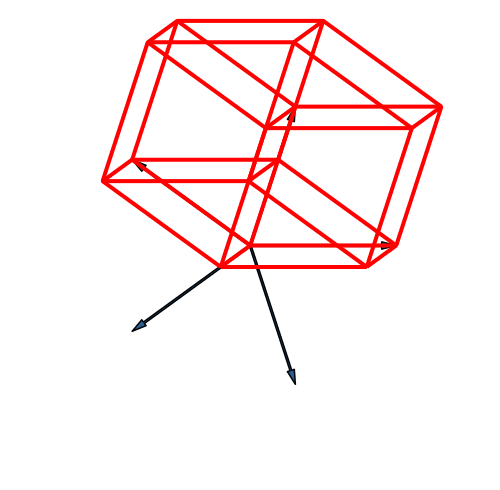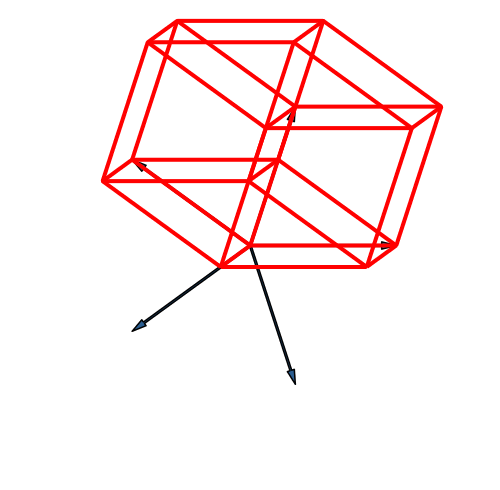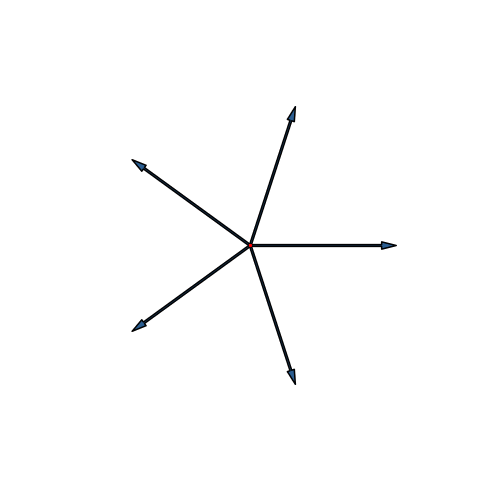
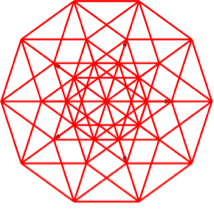
Abb. 20: Fünfdimensionaler Hyperwürfel. Stern-Lösung
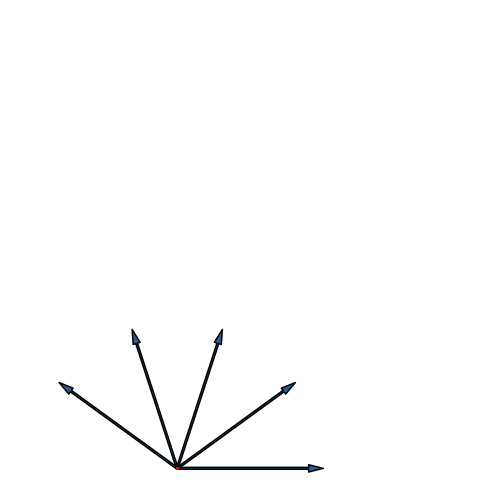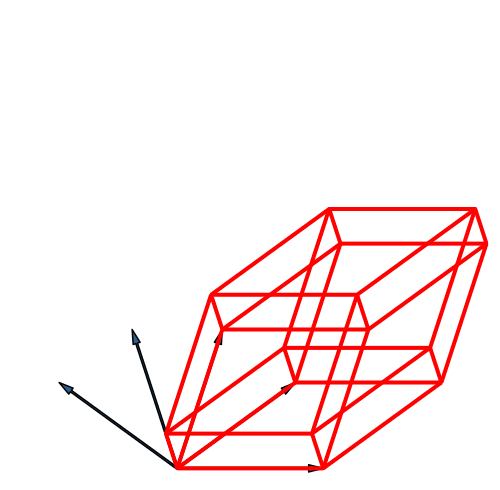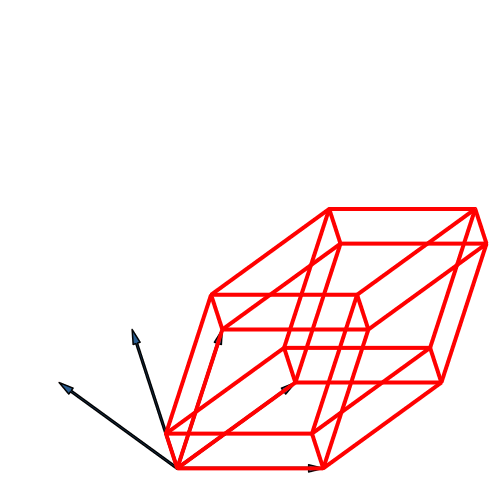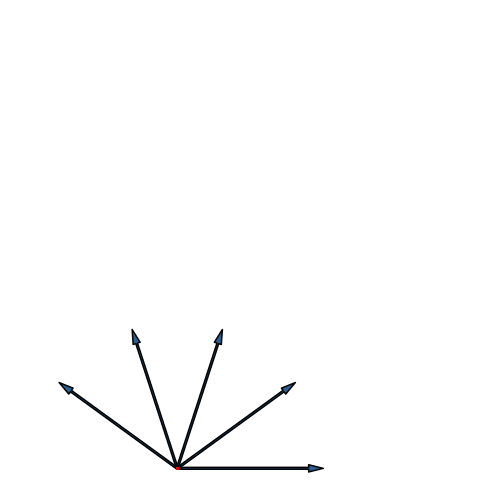
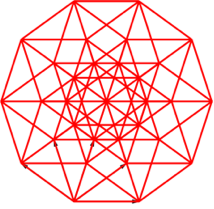
Abb. 21: Fünfdimensionaler Hyperwürfel. Fächer-Lösung
Der fünfdimensionale Hyperwürfel hat 25 = 32 Eckpunkte. Wir sehen zunächst drei Kreise mit je 10 Punkten, macht zusammen 30. Der Mittelpunkt zählt doppelt. Das sieht man auch daran, dass dort zehn Kanten einmünden, bei den übrigen Eckpunkten nur je fünf.
4.6 Sechsdimensionaler Hyperwürfel
Bei der Stern-Lösung (Abb. 22) entsteht ein Dreiecksraster.
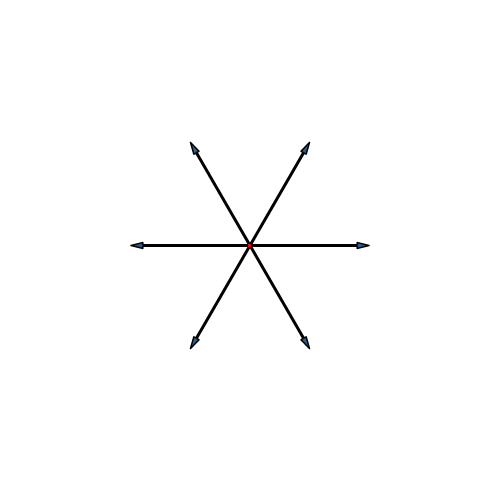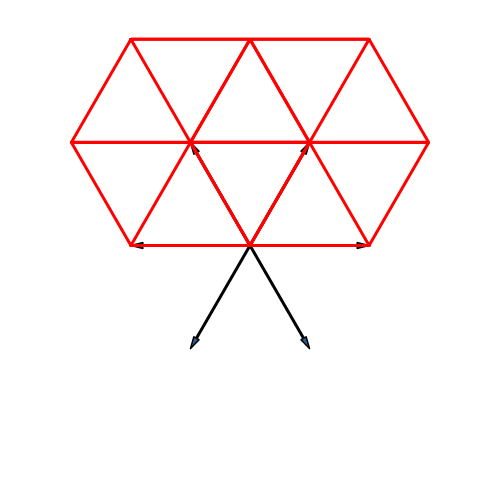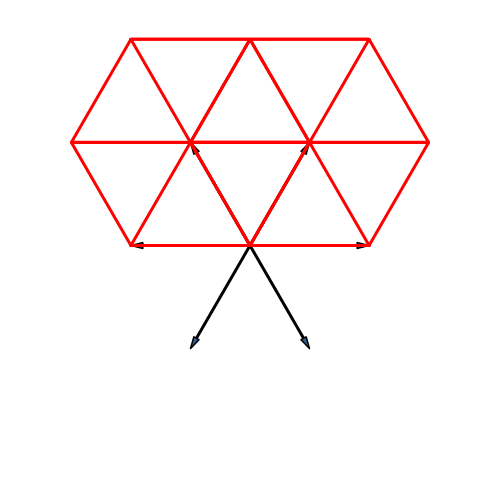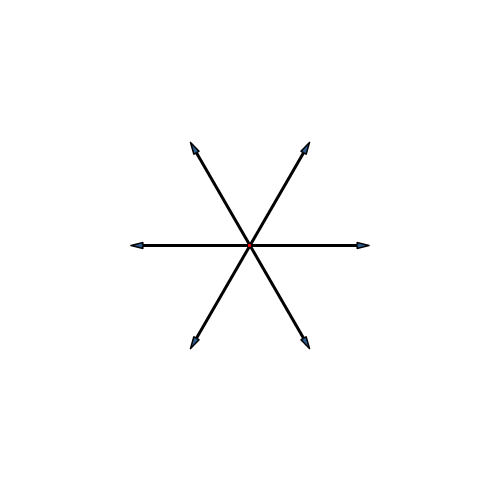
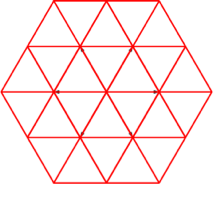
Abb. 22: Stern
Der sechsdimensionale Würfel hat 26 = 64 Eckpunkte. Die Verteilung der Punkte auf den Ecken des Dreiecksrasters finden wir wie folgt. Wir stören die Regelmäßigkeit etwas, aber nur so stark, dass die Rasterstruktur noch erkennbar bleibt (Abb. 23). Dazu habe ich die ersten fünf Winkel zwischen den sechs Pfeilen des Startsterns von 60° auf 55° reduziert.
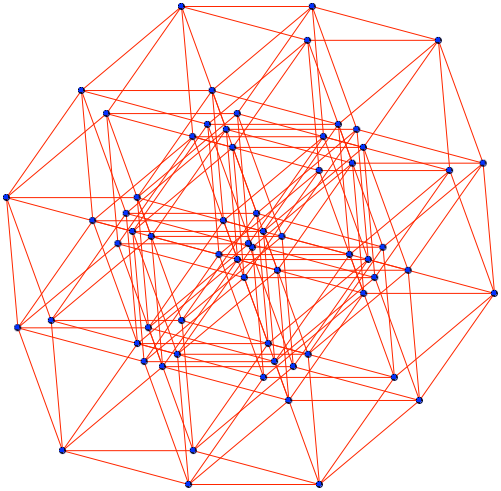
Abb. 23: Gestörte Regelmäßigkeit
Nun können wir die Vielfachheiten auszählen (Abb. 24). Mit etwas Fantasie können die Binomialkoeffizienten hineingesehen werden.
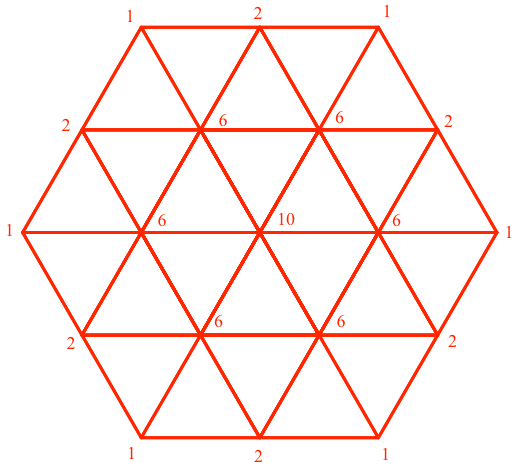
Abb. 24: Vielfachheiten
Die Fächer-Lösung sieht völlig anders aus (Abb. 25). Wir sehen drei Kreise mit je zwölf Eckpunkten und einen Kreis mit 24 Eckpunkten. Der zentrale Punkt ist vierfach zu zählen.
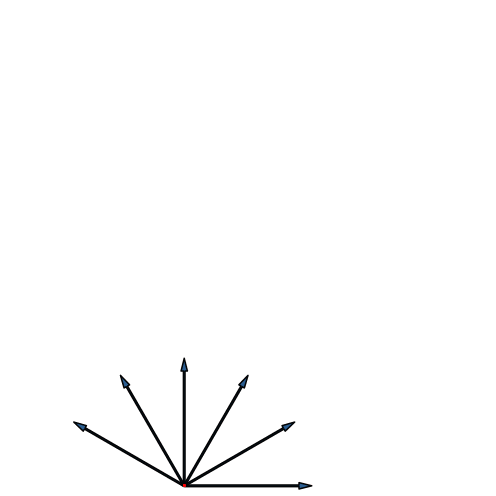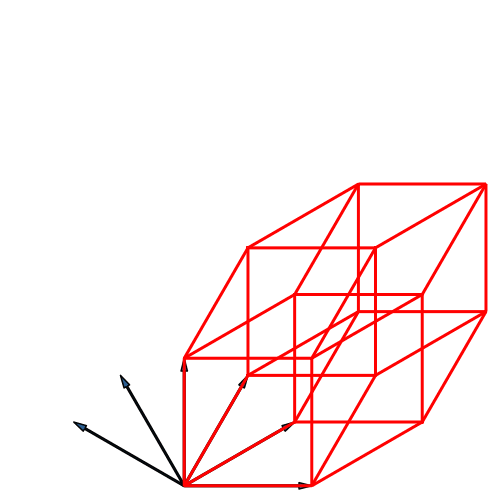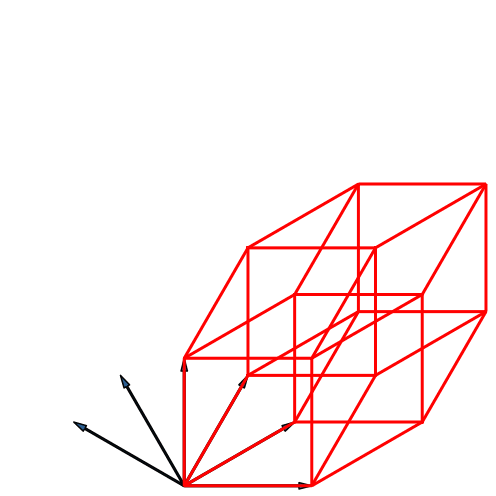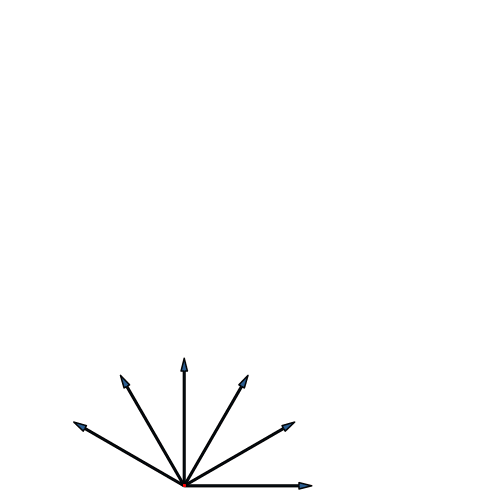
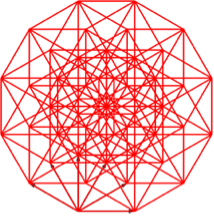
Abb. 25: Fächer-Lösung
4.7 Siebendimensionaler Hyperwürfel
In der Dimension sieben ist es wie in den Dimensionen drei und fünf. Die Endfiguren der Stern-Lösung (Abb. 26) und der Fächer-Lösung (Abb. 27) unterscheiden sich nicht.
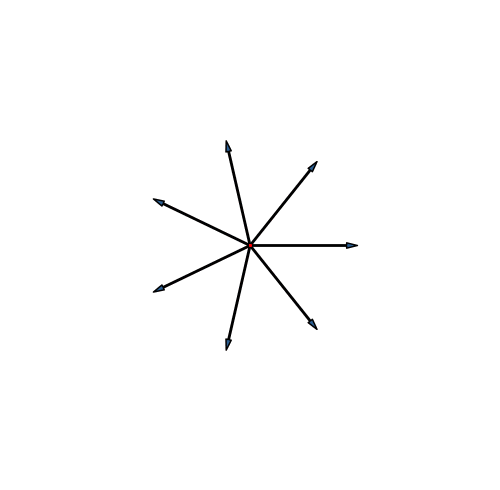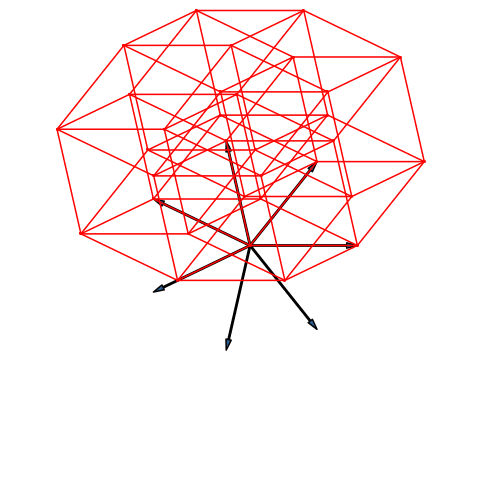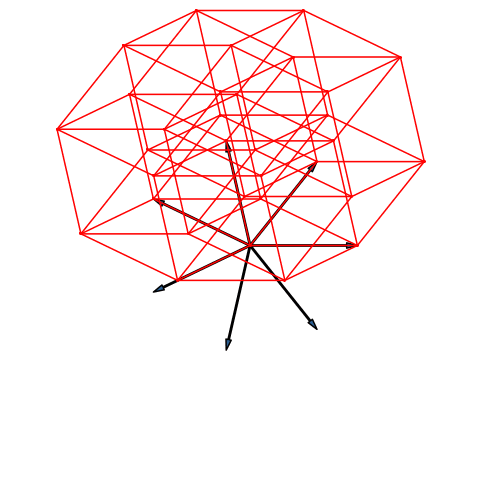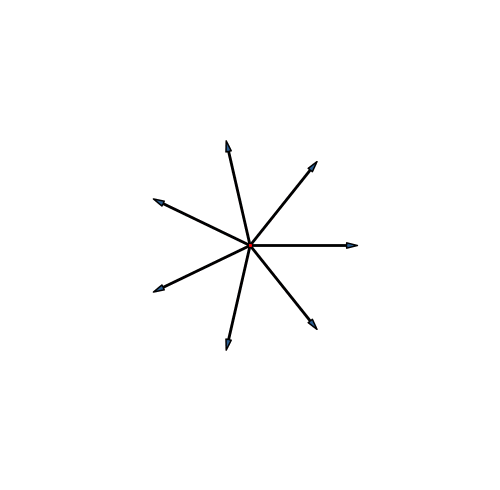
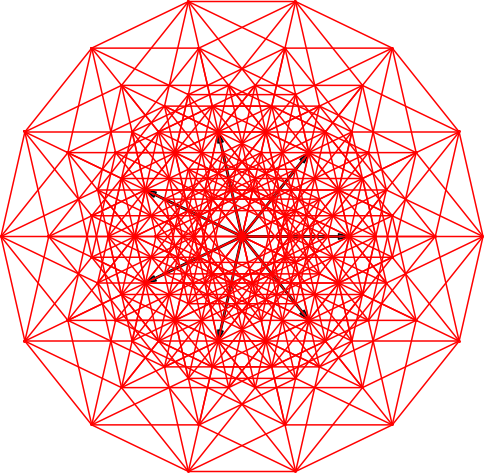
Abb. 26: Stern

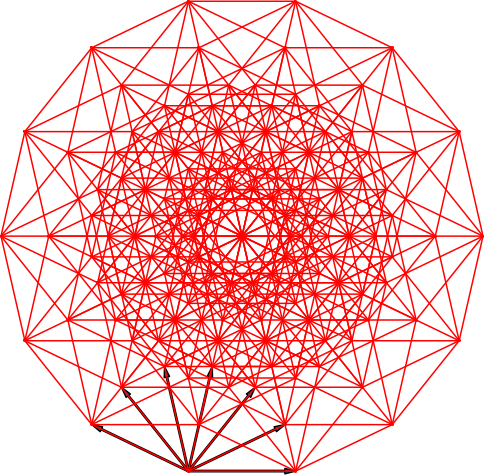
Abb. 27: Fächer
4.8 Achtdimensionaler Hyperwürfel
Die Abbildung 28 zeigt die Stern-Lösung für den achtdimensionalen Hyperwürfel. Der Umriss ist ein regelmäßiges Achteck.
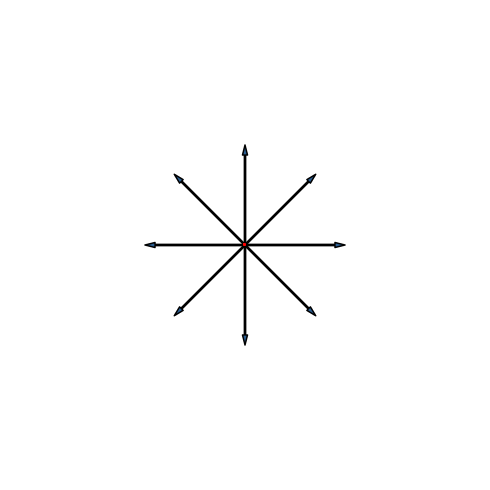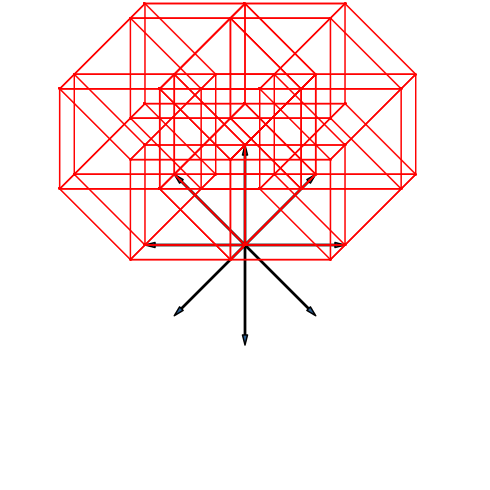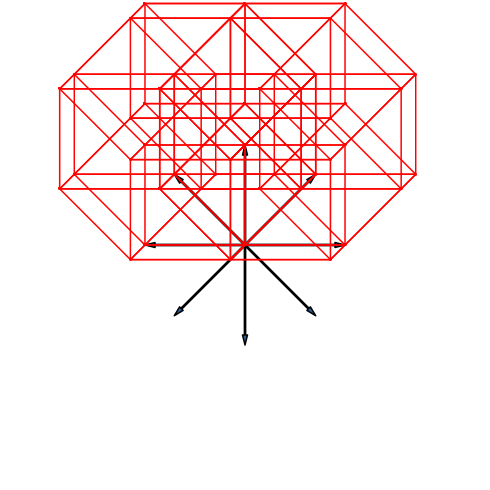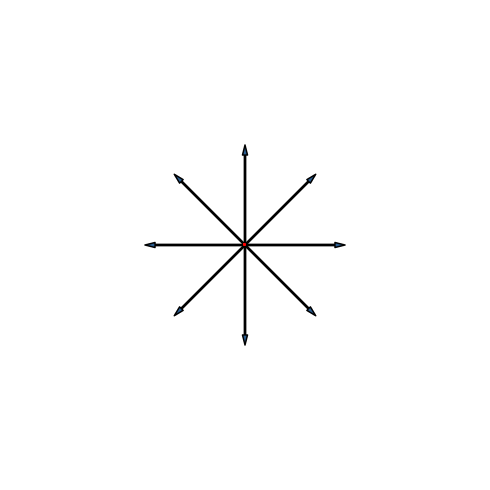
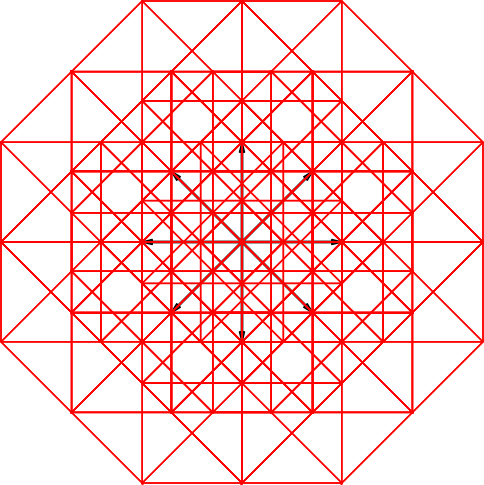
Abb. 28: Stern-Lösung
Die Stern-Lösung unterscheidet sich von der Fächer-Lösung (Abb. 29). Der Umriss ist ein regelmäßiges 16-Eck.

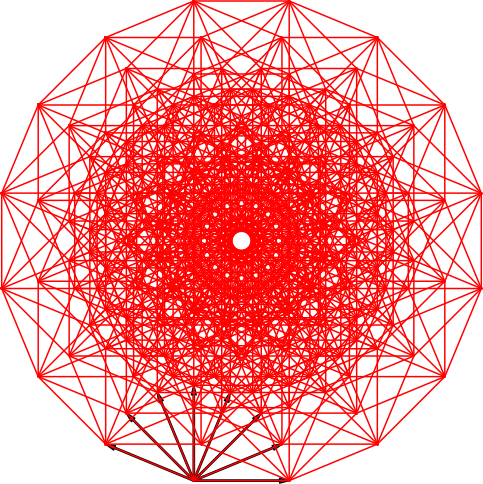
Abb. 29: Fächer-Lösung
4.9 Paritätsfrage
Wir haben ein unterschiedliches Verhalten bei gerader beziehungsweise ungerader Dimension n.
4.9.1 Gerade Dimension
Die Stern-Lösung ist anders als die Fächer-Lösung.
Die Stern-Lösung hat als Umriss ein regelmäßiges n-Eck.
Die Fächer-Lösung hat als Umriss ein regelmäßiges 2n-Eck.
4.9.2 Ungerade Dimension
Endfigur von Stern-Lösung und Fächer-Lösung sind gleich.
Der Umriss ist ein regelmäßiges 2n-Eck
5 3d-Darstellung von Hyperwürfeln
Wir können Hyperwürfel der Dimension n > 3 auch im dreidimensionalen Raum darstellen. Dazu wählen wir im Raum n möglichst symmetrisch angeordnete Vektoren und verfahren wie in der Ebene. Im Folgenden einige Beispiele.
5.1 Vierdimensionaler Hyperwürfel
Wir wählen die vier Vektoren vom Mittelpunkt eines regelmäßigen Tetraeders ausgehend zu den vier Ecken (Abb. 30). Diese Vektoren sind gleich lang und schließen paarweise den Winkel arccos(–⅓) ≈ 109.471° („kristallografischer Winkel“) ein.
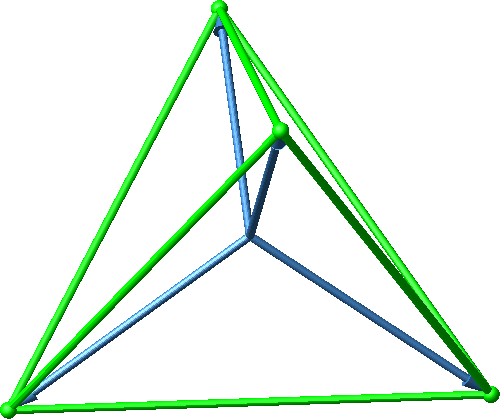

Abb. 30: Vier regelmäßig angeordnete Vektoren
Die Abbildungen 31 und 32 zeigen den Hyperwürfel. Es handelt sich hier sozusagen um die Stern-Lösung.
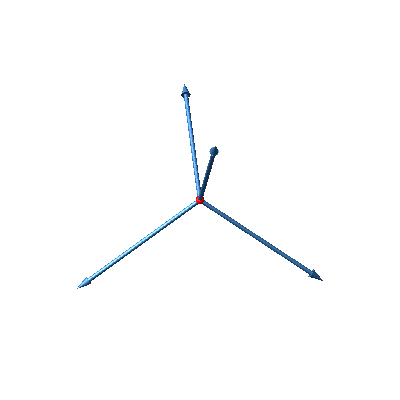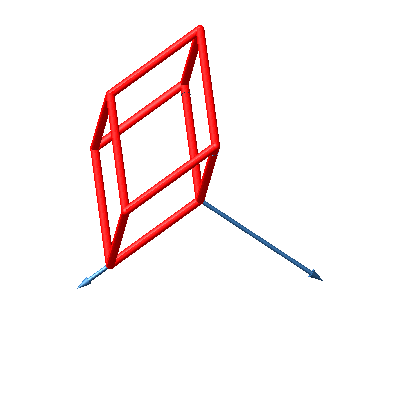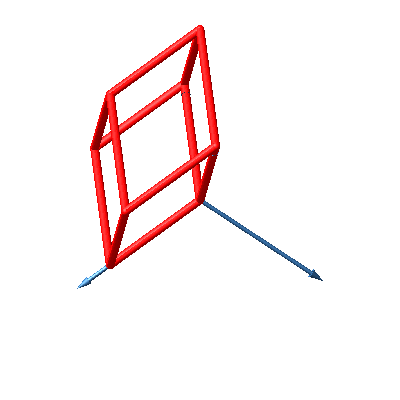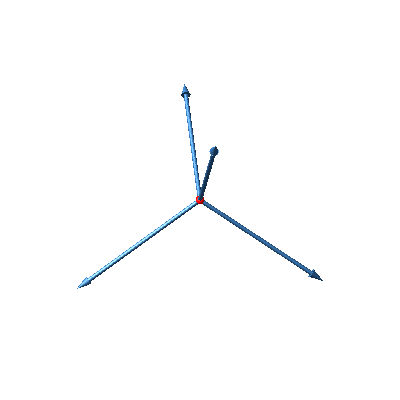
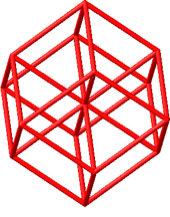
Abb. 31: Hyperwürfel

Abb. 32: Hyperwürfel
Die konvexe Hülle des Hyperwürfelmodells ist das Rhombendodekaeder. Zusätzlich geht von denjenigen Rhombendodekaeder-Ecken, bei denen nur drei Kanten zusammenkommen, eine vierte Kante zum Mittelpunkt. Das Rhombendodekaeder hat 8 + 6 = 14 Außenecken. Für den Hyperwürfel mit 24 = 16 Ecken muss zusätzlich der Mittelpunkt doppelt gezählt werden.
Die Abbildung 33 zeigt drei spezielle Sichten.
Das erste Beispiel ist die Sicht von oben (Drohnenperspektive). Wir erkennen den vierdimensionalen Hyperwürfel der Abbildungen 17 und 18.
Beim zweiten Beispiel haben wir die Sicht längs einer Mittelpunktsdiagonalen des Rhombendodekaeders. Das Beispiel sieht aus wie der dreidimensionale Würfel der Abbildungen 15 oder 16. Dabei besteht allerdings ein Dimensionsunterschied.
Beim dritten Beispiel sehen wir frontal einen unverzerrten Rhombus des Rhombendodekaeders.


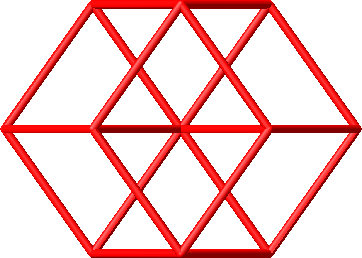
Abb. 33: Spezielle Sichten
Wir können die vier Vektoren statt in ein Tetraeder in einen Würfel einpassen (Abb. 34). Allerdings erscheinen jetzt zwei verschiedene Winkel als Zwischenwinkel zwischen den Winkelpaaren. Die beiden Winkel ergänzen sich aber auf 180°.
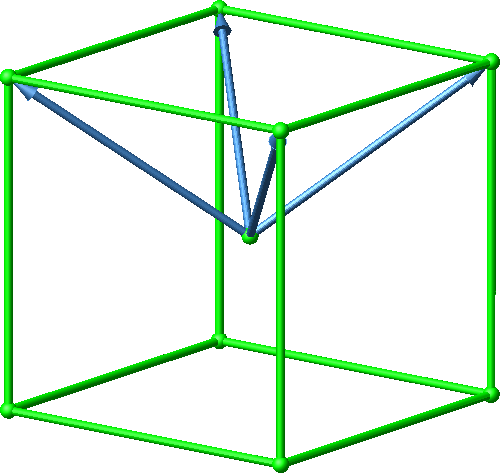
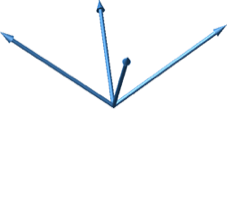
Abb. 34: Anordnung der vier Vektoren im Würfel
Die Abbildung 35 zeigt den zugehörigen Hyperwürfel. Die Endfigur ist wiederum das Rhombendodekaeder.
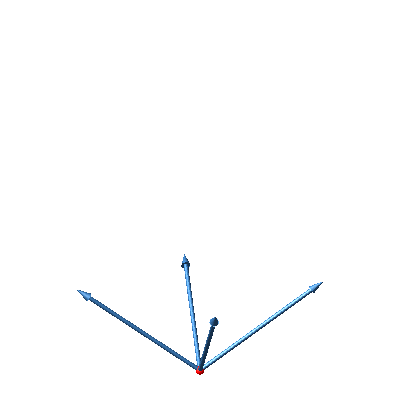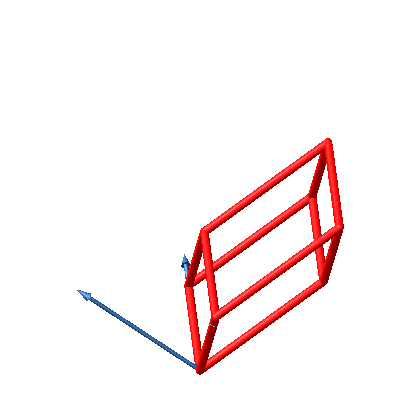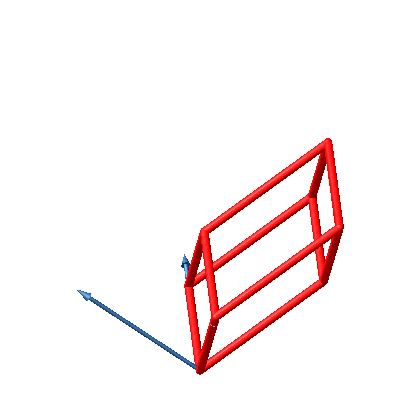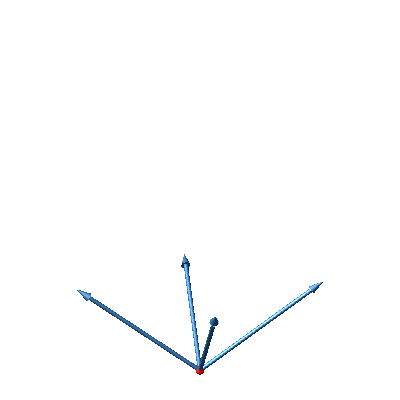
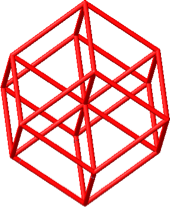
Abb. 35: Fächer-Lösung
5.2 Fünfdimensionaler Hyperwürfel
Es ist nicht möglich, fünf Vektoren im dreidimensionalen Raum so anzuordnen, dass sie paarweise denselben Winkel einschließen.
Wir wählen fünf Vektoren wie folgt (Abb. 36). Gegenüber der Horizontalebene haben sie die Steigung ½ . Von oben gesehen sind sie gleichmäßig verteilt.
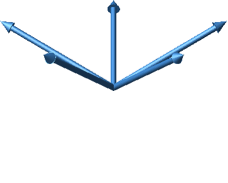
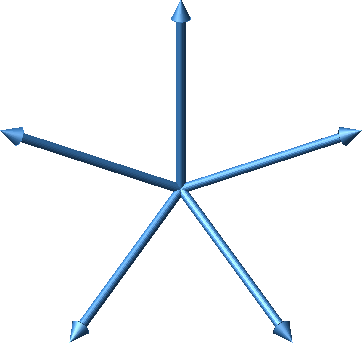
Abb. 36: Die fünf Vektoren
Die Abbildung 37 zeigt den zugehörigen fünfdimensionalen Hyperwürfel.
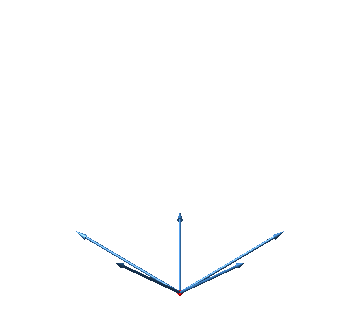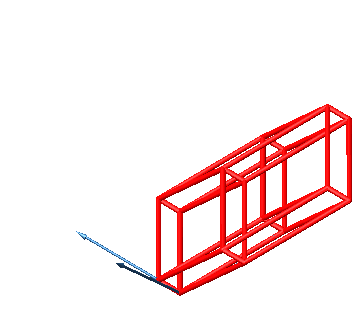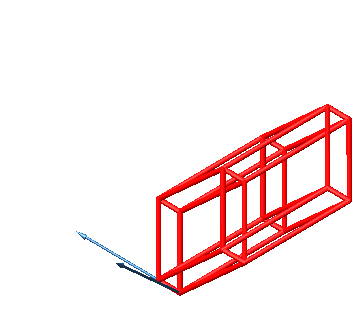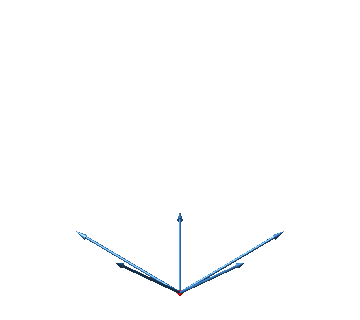

Abb. 37: Fünfdimensionaler Hyperwürfel im dreidimensionalen Raum
Die konvexe Hülle der Figur ist das Rhombenikosaeder. Seine Seitenflächen sind Rhomben, deren Diagonalen im Verhältnis des Goldenen Schnittes stehen.
Die Abbildungen 38 und 39 zeigen vier spezielle Sichten. Bei der Sicht von oben (Abb. 38, erstes Beispiel) sehen wir dieselbe Figur wie bei der zweidimensionalen Darstellung des fünfdimensionalen Hyperwürfels (Abb. 20 und 21). Das zweite Beispiel der Abbildung 38 zeigt eine Sicht von der Seite.
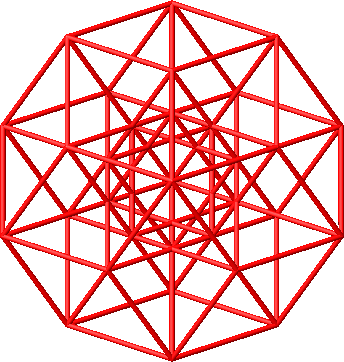
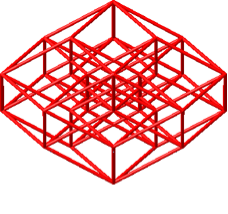
Abb. 38: Sicht von oben und von der Seite
Das erste Beispiel der Abbildung 39 zeigt ebenfalls eine Sicht von der Seite, die Figur wurde aber um 18° gedreht. Im zweiten Beispiel der Abbildung 39 haben wir die Sicht in Richtung eines der fünf Vektoren.
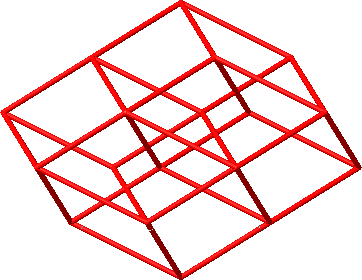
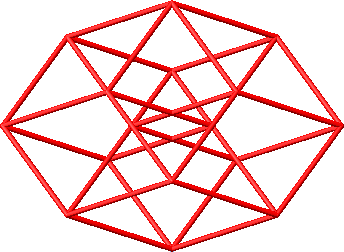
Abb. 39: Spezielle Sichten
Nun wählen wir die fünf Vektoren steiler, mit der Steigung 1 gegenüber der Horizontalebene (Abb. 40).
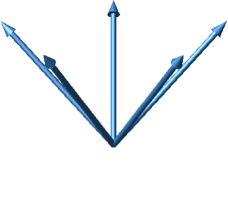
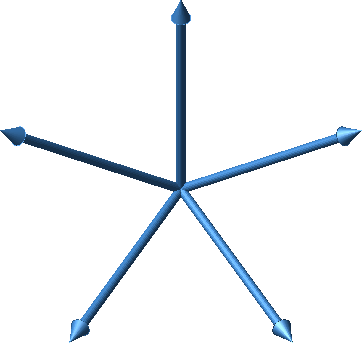
Abb. 40: Steile Vektoren
Die Abbildung 41 zeigt die entsprechende Darstellung des fünfdimensionalen Hyperwürfels.
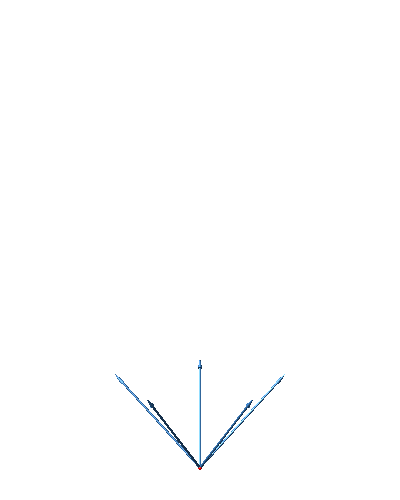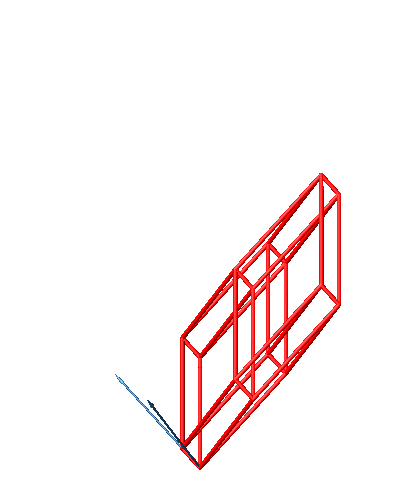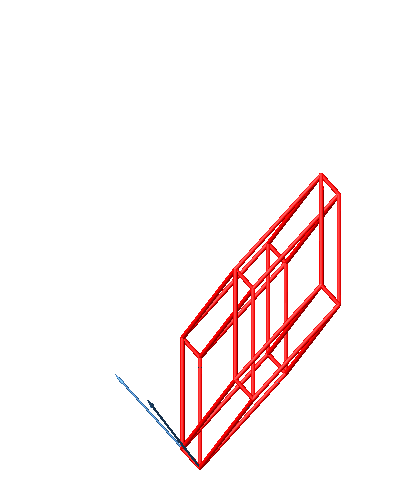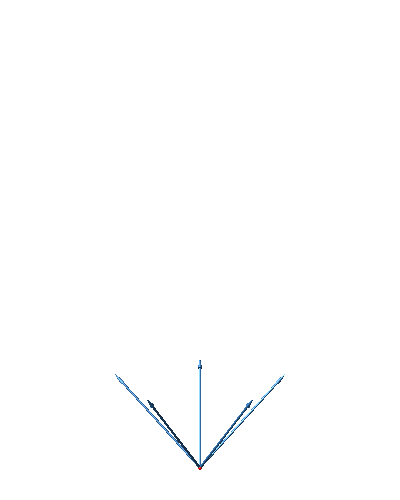
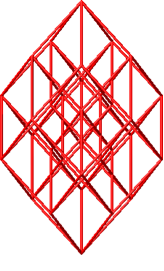
Abb. 41: Fünfdimensionaler Hyperwürfel
5.3 Sechsdimensionaler Hyperwürfel
Wir wählen sechs Vektoren so, dass sie vom Mittelpunkt ausgehend die Richtungen der sechs Mittelpunktdiagonalen des Ikosaeders haben (Abb. 42).
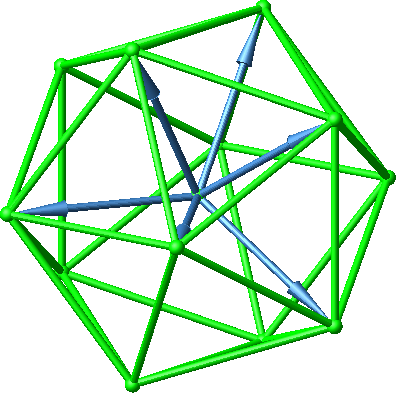

Abb. 42: Sechs Vektoren im Ikosaeder
Die Abbildung 43 zeigt die zugehörige Darstellung des sechsdimensionalen Hyperwürfels. Die konvexe Hülle ist das Rhombentriakontaeder.
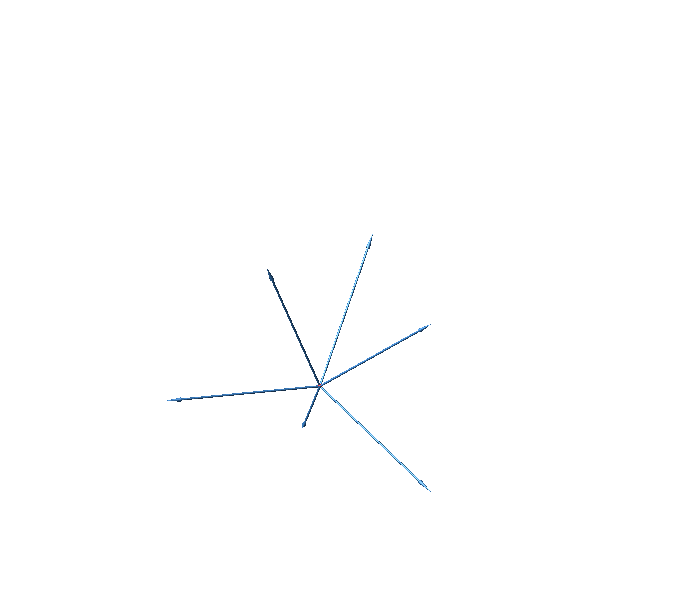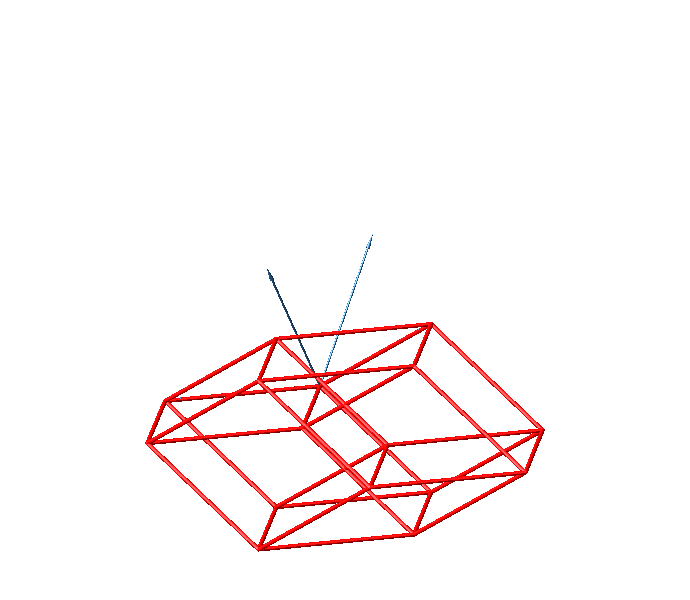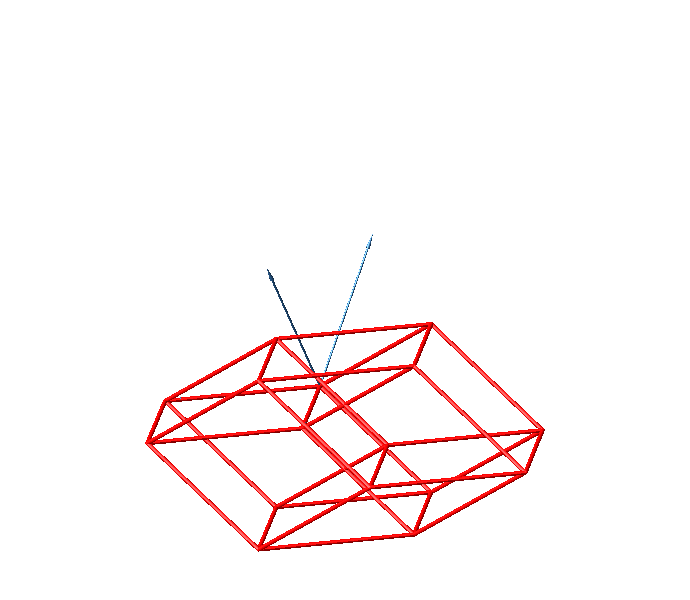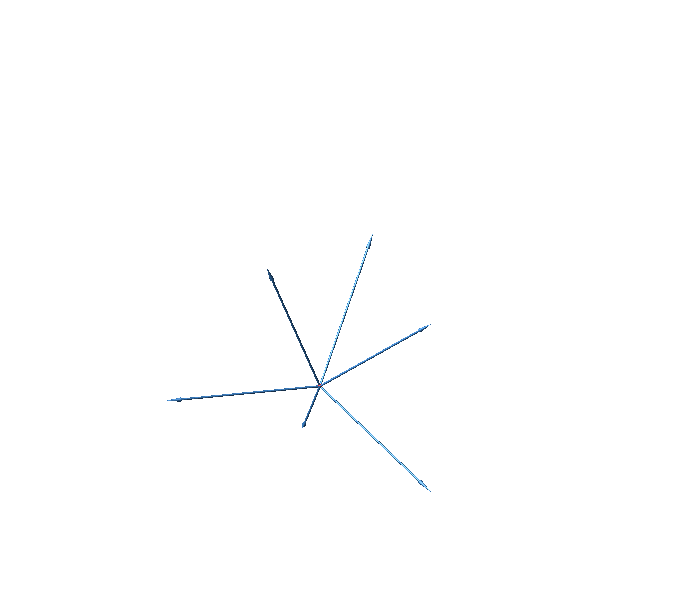
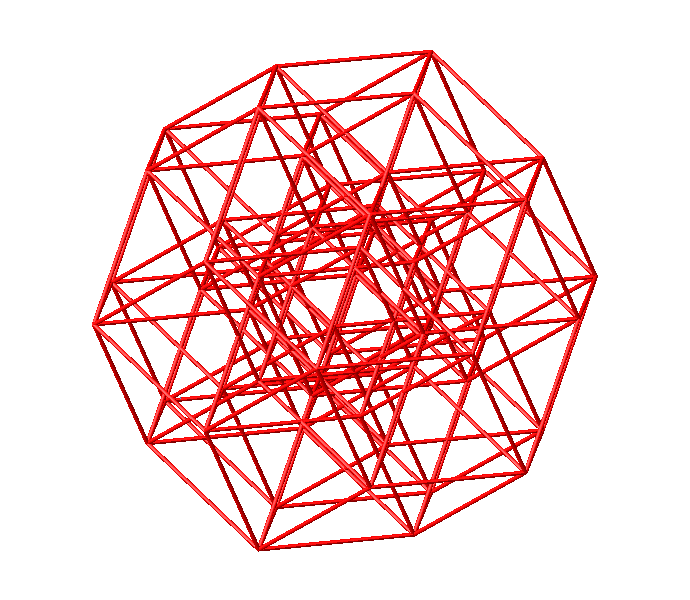
Abb. 43: Sechsdimensionaler Hyperwürfel
Im Folgenden einige spezielle Sichten.
Die Abbildung 44 zeigt die Sicht von oben, bezogen auf das für die Vektoren relevante Ikosaeder.
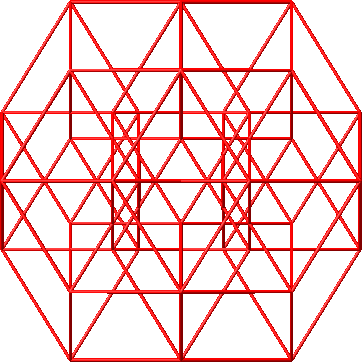
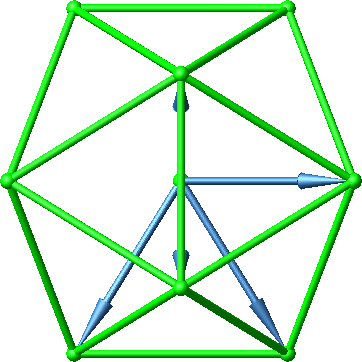
Abb. 44: Sicht von oben
Die Abbildung 45 zeigt die Sicht auf eine Dreiecksfläche des definierenden Ikosaeders.

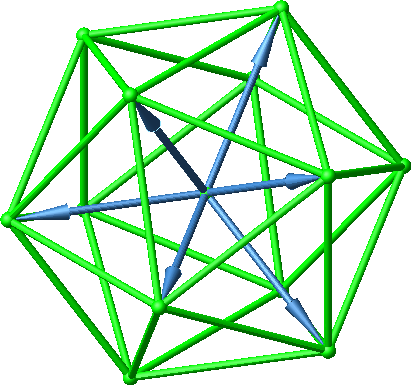
Abb. 45: Sicht auf eine Dreiecksfläche
Die Abbildung 46 schließlich zeigt die Sicht in Richtung eines der Vektoren, also einer Mittelpunktdiagonalen des Ikosaeders. Dabei geht fürs Auge eine Dimension verloren, wir daher meinen einen fünfdimensionalen Hyperwürfel (Abb. 20, 21, 38) zu sehen.
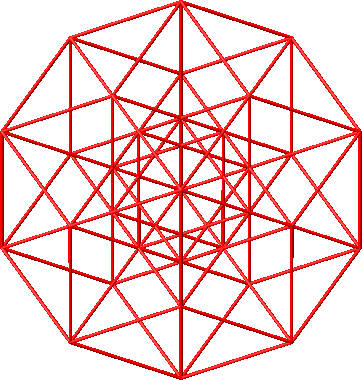
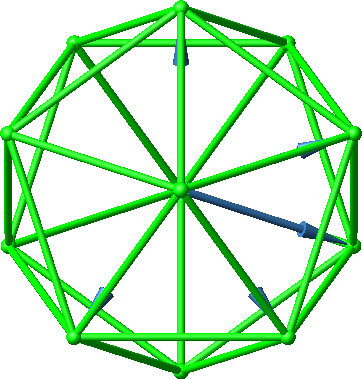
Abb. 46: Sicht in einer Vektorenrichtung
Weblinks
Hans Walser: Hyperwürfel
http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel3/Hyperwuerfel3.html
Hans Walser: Diagonalen im Hyperwürfe
Hans Walser: Hyperwürfel
http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel2/Hyperwuerfel2.htm
Hans Walser: Hypercubus
http://www.walser-h-m.ch/hans/Miniaturen/H/Hyperwuerfel/Hyperwuerfel.pdf