Hans Walser, [20221111]
Pythagoreische Dreiecke
Idee und Anregung: Maik Rentsch
1 Worum geht es?
Visualisierung der üblichen Parametrisierung der pythagoreischen Dreiecke mit Hilfe einer Ellipse.
2 Erinnerung
Mit
ist
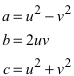
ein primitives pythagoreisches Tripel. Die Zahlen u und v heißen die Parameter des pythagoreischen Tripels und des zugehörigen pythagoreischen Dreieckes.
Die Tabelle 1 zeigt die ersten Werte.
|
u |
v |
a |
b |
c |
|
2 |
1 |
3 |
4 |
5 |
|
3 |
2 |
5 |
12 |
13 |
|
4 |
1 |
15 |
8 |
17 |
|
4 |
3 |
7 |
24 |
25 |
|
5 |
2 |
21 |
20 |
41 |
|
5 |
4 |
9 |
40 |
41 |
Tab. 1: Pythagoreische Tripel
3 Konstruktionsweg
Der folgende Konstruktionsweg gilt für beliebige Parameter u und v, in den Abbildungen wird mit u = 2 und v = 1 gearbeitet.
Wir beginnen mit einem rechtwinkligen Dreieck PQR mit den Katheten u und v gemäß Abbildung 1.
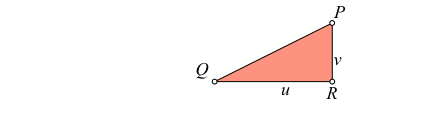
Abb. 1: Start mit einem rechtwinkligen Dreieck
Wir zeichnen nun einen Kreis k um Q mit dem Radius der Hypotenuse des Dreiecks PQR (Abb. 2). Diesen Kreis schneiden wir mit der Geraden QR. Die beiden Schnittpunkte F und G werden später als Brennpunkte einer Ellipse verwendet.
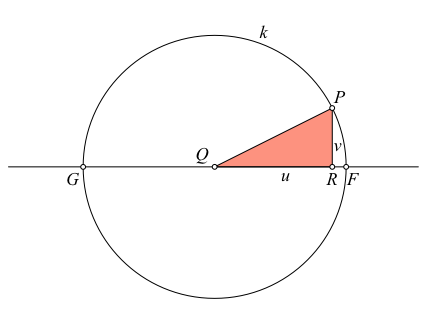
Abb. 2: Konstruktion der Brennpunkte
Mit dem Kreis i um R mit dem Radius v konstruieren wir die auf der Geraden QR die beiden Punkte E und H (Abb. 3). Der Punkt E wird zum Scheitelpunkt der Ellipse.
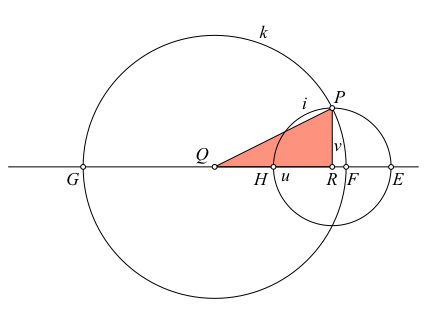
Abb. 3: Scheitelpunkt
Wir zeichnen nun die Ellipse e mit den Brennpunkten F und G und dem Scheitelpunkt E (Abb. 4). Diese Ellipse e schneiden den Kreis k in vier Punkten A, B, C, D.
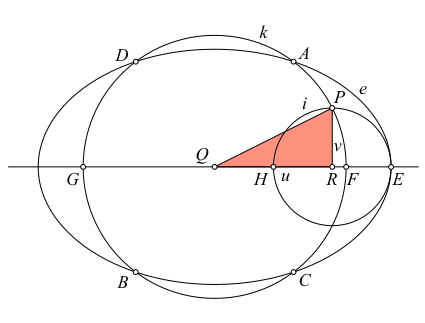
Abb. 4: Ellipse und vier Schnittpunkte
Exkurs: Alternativ können wir auch mit der Hyperbel h mit denselben beiden Brennpunkten F und G, aber dem Scheitelpunkt H arbeiten (Abb. 5). Es ergeben sich dieselben vier Schnittpunkte mit dem Kreis k. Ende Exkurs.
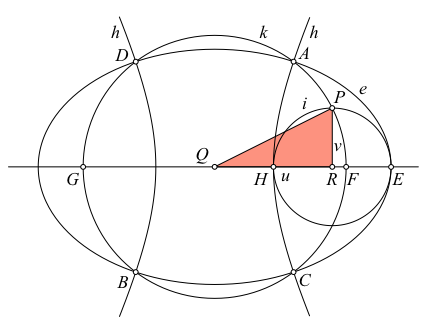
Abb. 5: Variante mit Hyperbel
Drei der vier Schnittpunkte definieren das zu den Parametern u und v gehörende pythagoreische Dreieck (Abb. 6).
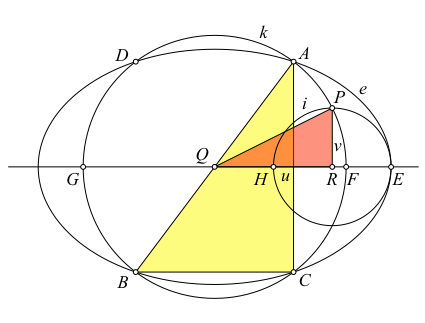
Abb. 6: Pythagoreisches Dreieck
4 Beweis
Wir arbeiten im kartesischen Koordinatensystem gemäß Abbildung 7.
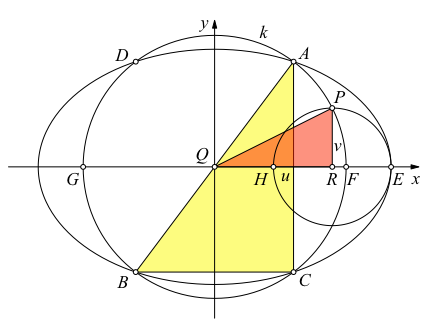
Abb. 7: Koordinatensystem
Die Ecken P, Q, R des rechtwinkligen Dreieckes haben die Koordinaten:
![]()
Die Hypotenuse, und das ist auch der Radius des Kreises k, hat die Länge:
![]()
Damit ergibt sich für den Kreis k die Kreisgleichung:
![]()
Für die Brennpunkte F und G ergeben sich die Koordinaten:
![]()
Für den Scheitelpunkt E erhalten wir:
![]()
Die Ellipse e hat die lange Halbachse u + v und die halbe Brennpunktweite:
![]()
Damit ergibt sich für die kurze Halbachse der Ellipse:
![]()
Die Ellipse e hat also die Gleichung:
![]()
Mit einiger Rechnung erhalten wir aus der Kreisgleichung und der Ellipsengleichung für die Schnittpunkte die Koordinaten:
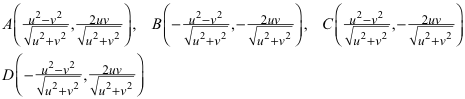
Somit ist:
![]()
Dies entspricht nicht den eingangs erwähnten Formeln für das pythagoreische Dreieck. Aber nach Skalierung mit dem Faktor
![]()
erhalten wir:
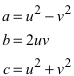
Unser Dreieck hat also dieselbe Form wir das pythagoreische Dreieck.
Weblinks
Hans Walser: Pythagorean Triangles
http://www.walser-h-m.ch/hans/Miniaturen/P/Pythagorean_Triangles/Pythagorean_Triangles.htm
Hans Walser: Pythagoreische Dreiecke
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke/Pyth_Dreiecke.htm
Hans Walser: Pythagoreische Dreiecke
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke2/Pyth_Dreiecke2.htm
Hans Walser: Pythagoreische Dreiecke
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke3/Pyth_Dreiecke3.htm
Hans Walser: Pythagoreische Dreiecke
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke4/Pyth_Dreiecke4.htm
Hans Walser: Pythagoreische Dreiecke
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dreiecke5/Pyth_Dreiecke5.html
Hans Walser: Pythagoreische Dreiecke falten
http://www.walser-h-m.ch/hans/Miniaturen/P/Pyth_Dr_falten/Pyth_Dr_falten.htm