Hans Walser, [20160915], [20180205]

Kreisausschöpfung

Anregung: Chr. H., O.

1 Worum geht es?

Es werden falsche und richtige Methoden der Kreis- und Kugelberechnung besprochen.

2 Kreis

2.1 Kreisfläche

Ein altgedienter Trick zur approximativen Bestimmung der Kreisfläche besteht darin einen Kreis auf Karopapier zu zeichnen und die Karos auszuzählen.

Die Abbildung 1.1 zeigt die Situation für 1, 2 und 3 Karolängen als Radius.

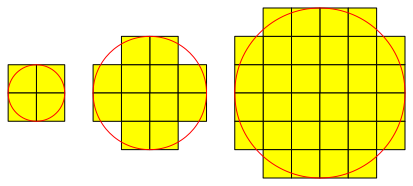
Abb. 1.1: Radien 1, 2, 3

Wir zählen jeweils diejenigen Quadrate, deren Mittelpunkt innerhalb des Kreises liegen. Dabei stellt sich die Frage nach den Mittelpunkten, die genau auf dem Kreis liegen. Hier kann Entwarnung gegeben werden: Dieser Fall kann nicht vorkommen. Mathematisch: Es gibt keinen Punkt mit zwei echt halbzahligen Koordinaten, der vom Ursprung einen ganzzahligen Abstand hat (Walser 2016).

In der Abbildung 1.2 haben wir die Radien 4 und 5.

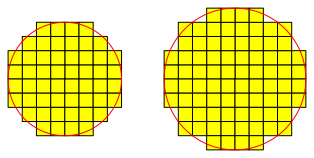
Abb. 1.2: Radien 4 und 5

In der Abbildung 1.3 haben wir den Radius 10.

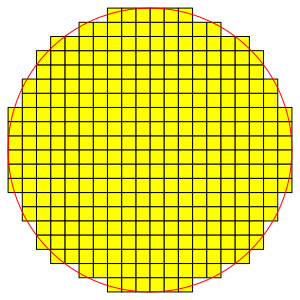
Abb. 1.3: Radius 10

Die Tabelle 1 zeigt die Resultate des Auszählens.

Um die Kreiszahl π approximativ zu bestimmen, müssen wir die Anzahl der Karos durch das Quadrat des Radius dividieren.

Radius	Anzahl Karos	Approx. π
1	4	4.
2	12	3.
3	32	3.555555556
4	52	3.250000000
5	80	3.200000000
6	112	3.111111111
7	156	3.183673469
8	208	3.250000000
9	256	3.160493827
10	316	3.160000000
100	31428	3.142800000
1000	3141676	3.141676000
10000	314159388	3.141593880

Tab. 1: Approximation der Kreiszahl π

2.2 Innensumme und Außensumme

Unser Zählkriterium für ein einzelnes Karo war die Position seines Mittelpunktes. Deshalb haben wir Karos, die nur teilweise im Kreis liegen und mitgezählt wurden, und andererseits auch Karos, die nicht mitgezählt wurden, obwohl sie teilweise im Kreis liegen.

Nach den Regeln der Kunst hätten wir mit Innensumme und Außensumme arbeiten müssen. Die Innensumme ist die Anzahl derjenigen Karos, die im Kreis enthalten sind. Die Außensumme ist die Anzahl derjenigen Karos, die als Gesamtfigur den Kreis enthalten. Die Abbildung 2 illustriert für den Radius 10 Innen- und Außensumme.

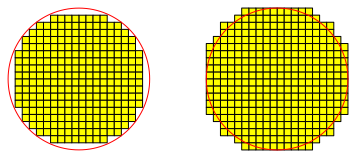
Abb. 2: Innen- und Außensumme

Die Tabelle 2 zeigt die entsprechenden Anzahlen und Approximationen von π.

Radius	Innensumme	Approx. π	Außensumme	Approx. π
1	0	0.	4	4.
2	4	1.	16	4.
3	16	1.777777778	36	4.
4	32	2.	60	3.750000000
5	60	2.400000000	88	3.520000000
6	88	2.444444444	132	3.666666667
7	120	2.448979592	172	3.510204082
8	164	2.562500000	224	3.500000000
9	216	2.666666667	284	3.506172840
10	276	2.760000000	344	3.440000000
100	31016	3.101600000	31796	3.179600000
1000	3137548	3.137548000	3145520	3.145520000
10000	314119052	3.141190520	314199016	3.141990160

Tabelle 2: Innen- und Außensumme

Da der Kreis keine pathologische Kurve ist, dürfen wir ruhig nach dem ersten Verfahren mit den Karomittelpunkten arbeiten.

2.3 Kreisumfang

Nachdem sich die Flächenbestimmung mit den Karos recht bewährt hat, könnte man in Versuchung geraten, dieselben Karofiguren für die Bestimmung des Kreisumfanges zu verwenden.

Wir zählen dazu die Umfangstrecken bei den Abbildungen 1.1 bis 1.3 und berechnen das Verhältnis zum Kreisdurchmesser (Tab. 3).

Radius	Umfang	Approx. π
1	8	4.
2	16	4.
3	24	4.
4	32	4.
5	40	4.
6	48	4.
7	56	4.
8	64	4.
9	72	4.
10	80	4.
100	800	4.
1000	8000	4.
10000	80000	4.

Tab. 3: Falsche Umfangberechnung

Da ist etwas schief gelaufen, oder vielmehr waagerecht und senkrecht statt schräg. Das erklärt auch den Fehler.

Wir erhalten viermal die Querschnittslänge (Durchmesser) als Umfang statt nur π-mal. Das ist die Sicht von links, rechts, oben und unten.

3 Kugel

3.1 Kugelvolumen

Wir arbeiten mit Einheitswürfeln. Die Abbildung 3.1 zeigt die Situation für den Radius 10. Das Kriterium für die Aktivierung eines Würfelchens ist die Position seines Mittelpunktes.

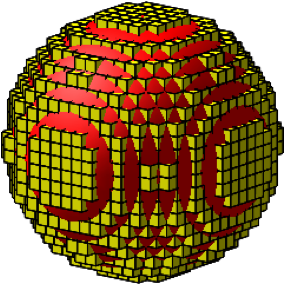
Abb. 3.1: Kugel im Würfelraster

In der Abbildung 3.2 sind die Würfel im Sinne eines dreidimensionalen „Schachbrettes“ mit verschiedenen Farben eingetragen. Würfel mit gemeinsamer Seitenfläche haben unterschiedliche Farben. Würfel mit gemeinsamer Kante haben gleiche Farben. Würfel mit gemeinsamer Ecke haben unterschiedliche Farben.

Abb. 3.2: Kugel im dreidimensionalen Schachbrett

In der Abbildung 4 ist die Kugel weggelassen worden. Wer Lust hat, kann das mit Würfelchen nachbauen. Wir brauchen dazu 4224 Würfelchen (Tab. 4)

Abb. 4.1: Nur Würfelchen

Abb. 4.2: Im dreidimensionalen Schachbrett

Die Abbildung 4.3 zeigt eine Kugel mit dem Radius 30 im dreidimensionalen Schachbrett approximiert.

Abb. 4.3: Kugel mit Radius 30

Nun geht’s wieder ans Auszählen (Tab. 4). Das Zählkriterium ist die Position des jeweiligen Würfelmittelpunktes.

Radius	Anzahl Würfelchen	Quotient
1	8	8.
2	32	4.
3	136	5.037037037
4	280	4.375000000
5	552	4.416000000
6	912	4.222222222
7	1472	4.291545190
8	2176	4.250000000
9	3112	4.268861454
10	4224	4.224000000
100	4188896	4.188896000
1000	4188806000	4.188806000

Tab. 4: Anzahl Würfelchen

Wenn wir die Anzahl der Würfelchen durch die dritte Potenz des Radius dividieren, approximieren wir den Wert . Unsere ausgezählten Werte sind fast alle etwas zu hoch.

3.2 Kugeloberfläche

Wiederum falsch ist es, die Oberfläche des Polyeders der Abbildung 4 mit der Kugeloberfläche gleichzusetzen. Das Polyeder der Abbildung 4 hat als Oberfläche sechsmal die Werte der Tabelle 1. Wir sehen von vorne, hinten, links, rechts, unten und oben je den Kreis im Karoraster. Diese falsche Methode liefert also sechsmal die Querschnittsfläche der Kugel als deren Oberfläche. Die richtige Kugeloberfläche ist nur viermal die Querschnittsfläche.

4 Ausblick

Für das nd-Volumen funktioniert die Auszählmethode. Für die Hyperoberfläche wird sie falsch.

Die Tabelle 5 gibt die Anzahlen für die Dimension 4. Der Quotient mit der vierten Potenz des Radius sollte ergeben (man beachte das Quadrat beim π).

Radius	Anzahl Hyperwürfelchen	Quotient
1	16	16.
2	80	5.
3	512	6.320987654
4	1312	5.125000000
5	3312	5.299200000
6	6480	5.
7	12288	5.117867555
8	20352	4.968750000
9	33392	5.089468069
10	49648	4.964800000
11	73408	5.013865173
12	102176	4.927469136
13	142256	4.980777984
14	190544	4.960016660
15	253088	4.999269136
16	324448	4.950683594
17	414768	4.966032495
18	517776	4.932327389
19	645888	4.956131399
20	790400	4.940000000

Tab. 5: Anzahl Hyperwürfelchen

Im vierdimensionalen Fall gibt es Hyperwürfelmittelpunkte die exakt auf der Hypersphäre liegen. So ist etwa:

(1)

Websites

Hans Walser: Unmögliche pythagoreische Dreiecke (17. 09. 2016):

www.walser-h-m.ch/hans/Miniaturen/U/Unmoegl_pyth_Dreiecke/Unmoegl_pyth_Dreiecke.htm