Hans Walser, [20160916], [20161009]
Unmšgliche pythagoreische Dreiecke
Ideen: Chr. Z., B.
1 Schwarze Quadrate
Woher kommen die beiden schwarzen Quadrate?
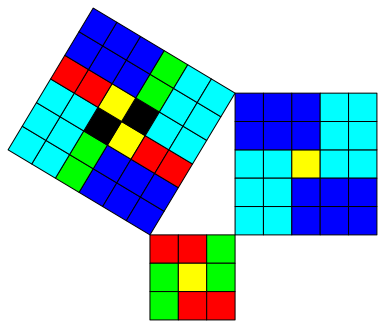
Abb. 1: Woher kommen die schwarzen Quadrate?
2 Sachverhalt
Es gibt kein pythagoreisches Dreieck mit ungeraden KathetenlŠngen a und b.
In hšheren Dimensionen sieht das unterschiedlich aus.
3 Beweis
Wir kšnnen den Beweis auf zwei Arten darstellen.
3.1 Modulo 4
Sei 
und 
.
Dann ist:
(1)
Es ist
also 
.
Das kann keine Quadratzahl sein, da Quadratzahlen bei Division durch 4 nur die
Reste 0 (gerade Quadratzahl) oder 1 (ungerade Quadratzahl) haben kšnnen.
3.2 Halbzahligkeit
Wir kšnnen den Beweis auch fźhren, indem wir die beteiligten Zahlen halbieren. Die Katheten a und b sind dann echt halbzahlig. In der Dezimaldarstellung enden sie auf ăPunkt fźnfŇ. Ihre Quadrate enden auf Punkt zwei fźnf, die Summe der Quadrate auf Punkt fźnf. Dies ist weder das Quadrat einer ganzen Zahl noch das Quadrat einer echten Halbzahl.
4 Im Raum
Das rŠumliche Analogon zum rechtwinkligen Dreieck ist das Orthoschem (Abb. 2).
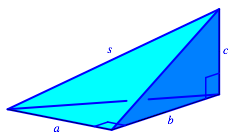
Abb. 2: Orthoschem
Das ist ein unregelmŠ§iges Tetraeder mit drei aufeinanderfolgenden paarweise senkrechten Kanten, die wir mit a, b, c bezeichnen. Fźr die lŠngste Tetraederkante s gilt dann:
(2)
Wir haben nun einen zur Ebene analogen Sachverhalt:
Es gibt kein pythagoreisches Orthoschem mit ungeraden Kanten a, b, c und ganzzahligem s.
Es ist nŠmlich:
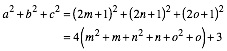(3)
Das kann keine Quadratzahl sein.
5 Hšhere Dimensionen
Im 4d-Raum ist es aber ganz anders. Das einfachste pythagoreische Orthoschem mit
(4)
ergibt sich durch
(5)
Die Tabelle 1 gibt einige weitere Lšsungen.
|
a |
b |
c |
d |
|
s |
|
1 |
1 |
1 |
1 |
|
2 |
|
3 |
3 |
3 |
3 |
|
6 |
|
5 |
3 |
1 |
1 |
|
6 |
|
5 |
5 |
5 |
5 |
|
10 |
|
7 |
5 |
5 |
1 |
|
10 |
|
7 |
7 |
1 |
1 |
|
10 |
|
7 |
7 |
7 |
7 |
|
14 |
|
9 |
3 |
3 |
1 |
|
10 |
|
9 |
9 |
5 |
3 |
|
14 |
|
9 |
9 |
9 |
9 |
|
18 |
|
11 |
5 |
5 |
5 |
|
14 |
|
11 |
7 |
5 |
1 |
|
14 |
|
11 |
11 |
9 |
1 |
|
18 |
|
11 |
11 |
11 |
11 |
|
22 |
Tab. 1: Im 4d-Raum
Fźr den 5d-Raum gibt es kein Beispiel. Um das einzusehen, mźssen wir modulo 8 rechnen. Die ungeraden Zahlen haben bei Division durch 8 die Reste 1, 3, 5 oder 7. Ihre Quadrate haben bei Division durch 8 immer den Rest 1. Die Summe źber die fźnf Quadratzahlen hat daher bei Division durch 8 den Rest 5 und kann keine Quadratzahl sein.
Fźr die Dimensionen 6 und 7 gibt es keine Lšsungen. Der Ausschluss erfolgt analog zu den Dimensionen 2 und 3.
Fźr die Dimension 8 gibt es Lšsungen. Die Tabelle 2 gibt einige Lšsungen an.
|
a |
b |
c |
d |
e |
f |
g |
h |
|
s |
|
3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
4 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
|
8 |
|
5 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
|
8 |
|
5 |
5 |
3 |
1 |
1 |
1 |
1 |
1 |
|
8 |
|
5 |
5 |
5 |
5 |
5 |
3 |
3 |
1 |
|
12 |
|
7 |
3 |
1 |
1 |
1 |
1 |
1 |
1 |
|
8 |
|
7 |
5 |
5 |
3 |
3 |
3 |
3 |
3 |
|
12 |
|
7 |
5 |
5 |
5 |
3 |
3 |
1 |
1 |
|
12 |
|
7 |
7 |
3 |
3 |
3 |
3 |
3 |
1 |
|
12 |
|
7 |
7 |
5 |
3 |
3 |
1 |
1 |
1 |
|
12 |
|
7 |
7 |
7 |
5 |
5 |
5 |
5 |
3 |
|
16 |
|
7 |
7 |
7 |
7 |
5 |
5 |
3 |
1 |
|
16 |
|
7 |
7 |
7 |
7 |
7 |
3 |
1 |
1 |
|
16 |
Tab. 2: Im 8d-Raum
Fźr die Dimension 9 gibt es ebenfalls Lšsungen (Tab. 3).
|
a |
b |
c |
d |
e |
f |
g |
h |
i |
|
s |
|
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
3 |
|
3 |
3 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
5 |
|
3 |
3 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
|
7 |
|
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
3 |
|
9 |
|
5 |
3 |
3 |
1 |
1 |
1 |
1 |
1 |
1 |
|
7 |
|
5 |
3 |
3 |
3 |
3 |
3 |
3 |
1 |
1 |
|
9 |
|
5 |
5 |
3 |
3 |
3 |
1 |
1 |
1 |
1 |
|
9 |
|
5 |
5 |
5 |
1 |
1 |
1 |
1 |
1 |
1 |
|
9 |
|
5 |
5 |
5 |
3 |
3 |
3 |
3 |
3 |
1 |
|
11 |
|
5 |
5 |
5 |
5 |
3 |
3 |
1 |
1 |
1 |
|
11 |
|
5 |
5 |
5 |
5 |
5 |
5 |
3 |
3 |
1 |
|
13 |
|
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
5 |
|
15 |
Tab. 3: Im 9d-Raum
6 Allgemein
Zu gegebenem n > 1 suchen wir n ungerade Zahlen u1, ... , un, deren Quadratsumme ebenfalls eine Quadratzahl ist:
(6)
Wir formen etwas um. Mit uk = 2mk –1 erhalten wir:
(7)
Der Term (7) hat bei Division durch 4 denselben Rest wie n. Wir machen daher eine Fallunterscheidung je nach dem Rest von n bei Division durch 4.
6.1 n kongruent zu 0 modulo 4
In diesem Fall gibt es immer eine Lšsung. Wir setzen n = 4p und kšnnen mit den ungeraden Zahlen
(8)
arbeiten:
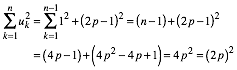(9)
Die Tabellen 1 und 2 zeigen aber, dass es noch weitere Lšsungen geben kann.
6.2 n kongruent zu 1 modulo 4
Wir machen eine Unterfallunterscheidung modulo 8. Zahlen, die kongruent zu 1 modulo 4 sind, sind modulo 8 kongruent zu 1 oder zu 5.
6.2.1 n kongruent zu 1 modulo 8
Wir zeigen, dass es zu n kongruent zu 1 modulo 8 immer eine Lšsung gibt.
Wir schreiben:
(10)
und:
(11)
Die Tabelle 4 illustriert, dass wir so tatsŠchlich alle benštigten Werte fźr m erhalten:
|
p \
q |
1 |
2 |
3 |
4 |
5 |
|
1 |
1 |
|
|
|
|
|
2 |
2 |
3 |
|
|
|
|
3 |
4 |
5 |
6 |
|
|
|
4 |
7 |
8 |
9 |
10 |
|
|
5 |
11 |
12 |
13 |
14 |
15 |
Tab. 4: Werte fźr m
Nun wŠhlen wir die ersten p – q ungeraden Zahlen als 3, die restlichen als 1.
Zu zeigen ist:
(12)
Fźr den Term links erhalten wir unter Einsetzen von (10) und (11):
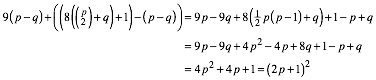(13)
Somit ist der Term links ein Quadrat. Dies war zu zeigen.
6.2.2 n kongruent 5 modulo 8
Ist n kongruent zu 5 modulo 8, dann ist die Summe (7) kongruent zu n modulo 8, also kongruent zu 5 modulo 8. Dies kann keine Quadratzahl sein.
6.3 n kongruent zu 2 oder zu 3 modulo 4
Der Term (7) kann keine Quadratzahl sein, da Quadratzahlen bei Division durch 4 nur die Reste 0 oder 1 haben kšnnen.
7 Zusammenfassung
Lšsungen gibt es genau fźr n kongruent zu 0 modulo 4 und fźr n kongruent 1 modulo 8.
Der Fall n = 1 ist trivial.
Zusammengefasst:
Lšsungen genau fźr n kongruent zu 0,
1 oder 4 modulo 8.
1, 4, 8, 9, 12, 16, 17, 20, 24, 25, 28, 32, 33, ... (14)