Hans Walser, [20170417]
Kollineare Punkte
1 Worum geht es?
Es werden drei Beispiele von kollinearen Punkten im Kontext des Inkreises eines Dreiecks vorgestellt. Die Beispiele wurden mit DGS verifiziert, mit einer Ausnahme fehlen aber Beweise im klassischen Sinn.
2 Inkreis
Zu einem beliebigen Dreieck zeichnen wir den Inkreis. Weiter zeichnen wir die Schnittpunkte des Inkreises mit den Verbindungsstrecken des Inkreis-Mittelpunktes zu den Dreiecksecken (Abb. 1). Diese Verbindungsstrecken liegen auf den Winkelhalbierenden.
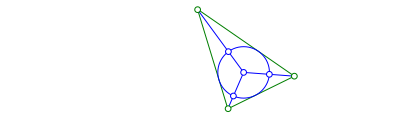
Abb. 1: Inkreis und Schnittpunkte auf den Winkelhalbierenden
3 Inkreissekanten
Wir zeichnen die drei durch diese drei Schnittpunkte definierten Sekanten und schneiden sie mit den VerlŠngerungen der Dreiecksseiten gemŠ§ Abbildung 2.
So erhalten wir drei kollineare Punkte.
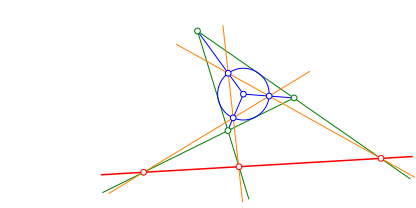
Abb. 2: Sekanten
4 Inkreistangenten
Wir zeichnen in den drei Schnittpunkten die Tangenten an den Inkreis (Abb. 3). Die Schnittpunkte mit den Dreieckseiten sind wiederum kollinear.
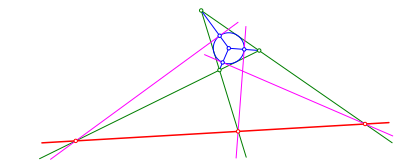
Abb. 3: Tangenten
Die beiden roten Geraden durch die drei kollinearen Punkte der Abbildungen 2 und 3 sind parallel (Abb. 4).
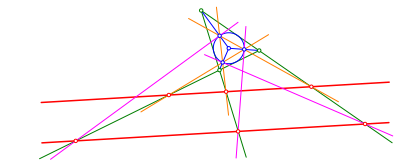
Abb. 4: Parallele Geraden
5 Sekanten und Tangenten
Mit den Sekanten und Tangenten finden wir ein drittes Tripel von kollinearen Punkten (Abb. 5).
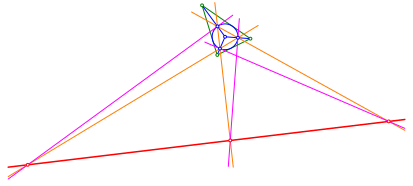
Abb. 5: Drittes Tripel von kollinearen Punkten
Allerdings ist diese dritte rote Gerade nicht mehr parallel zu den beiden anderen roten Geraden (Abb. 6).
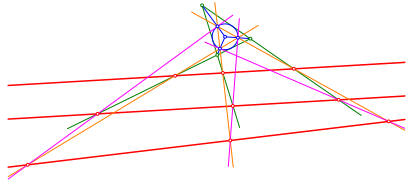
Abb. 6: †bersicht
6 Beweise
Fźr die ersten beiden Tripel kollinearer Punkte (Abb. 2 und 3) habe ich keinen Beweis gefunden.
Das letzte Tripel (Abb. 5) ist ein Sonderfall des Satzes von Pappos-Pascal. Dies kann eingesehen werden wie folgt. Siehe dazu auch [1].
Die Abbildung 7 zeigt die źbliche Konfiguration des Satzes von Pappos-Pascal. Als Kegelschnitt wurde eine Ellipse gezeichnet. In unserem Sonderfall ist es ein Kreis, der Inkreis.
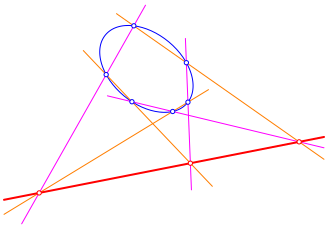
Abb. 7: Satz von Pappos-Pascal
Nun schieben wir die in der Abbildung 8 durch Doppelpfeile markierten Punkte zusammen.
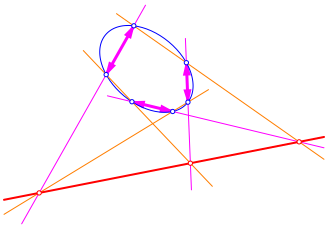
Abb. 8: Punkte zusammenschieben
Dadurch werden die magenta Sekanten zu Tangenten, und wir erhalten die Situation der Abbildung 5.
Das grźne Ausgangsdreieck und dessen Winkelhalbierende sind in diesen †berlegungen irrelevant.
Websites
[1] Hans Walser: Kollineare Punkte (19. 04. 2017):
www.walser-h-m.ch/hans/Miniaturen/K/Kollineare_Punkte1/Kollineare_Punkte1.htm