Hans Walser, [20230822]

Diagonalenlote

1 Worum es geht

Ecklote auf eine Rechteckdiagonale.

2 Die Kinematik

Die Abbildung 1 zeigt die Kinematik der Figur.

Abb. 1: Kinematik

3 Konstruktion

In einem Rechteck zeichnen wir eine der beiden Diagonalen (Abb. 2.1).

Abb. 2.1: Rechteck mit einer Diagonalen

Von den beiden anderen Ecken aus zeichnen wir die Lote auf die Diagonale (Abb. 2.2).

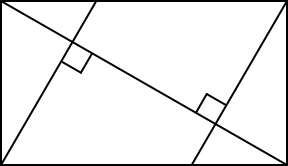
Abb. 2.2: Diagonalenlote

Wir können zwei rechtwinklige Dreiecke einpassen (gelb in Abb. 2.3).

Abb. 2.3: Gelbe rechtwinklige Dreiecke

Nun zeichnen wir Parallelen zur Diagonale gemäß Abbildung 2.4.

Abb. 2.4: Parallelen zur Diagonale

Wir können zwei weitere rechtwinklige Dreiecke einpassen (hellblau in Abb. 2.5).

Abb. 2.5: Hellblaue rechtwinklige Dreiecke

Es bleibt ein rechteckiges Loch übrig. Wir passen ein magenta Rechteck ein (Abb. 2.6).

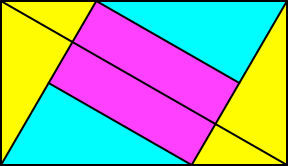
Abb. 2.6: Magenta Rechteck

Wir lassen die Höhe des Startrechteckes invariant und variieren die Länge, indem wir die Diagonale durch die Ecke links oben verdrehen.

4 Pausen

In der Kinematik der Abbildung 1 hat es mehrere Pausen bei geometrisch interessanten Situationen.

4.1 Startquadrat

Bei einem Seitenverhältnis 1 : 1 haben wir ein Quadrat (Abb. 3).

Abb. 3: Startquadrat

4.2 DIN-Format

Bei einem Seitenverhältnis √2 : 1 ergibt sich ein Rechteck im DIN-Format (Abb. 4). Das magenta Rechteck hat ebenfalls das Seitenverhältnis √2 : 1, ist also auch im DIN-Format.

Abb. 4: DIN-Format

Die oberste und die unterste Ecke des magenta Rechtecks stehen senkrecht übereinander (Abb. 5). Sie liegen auf der senkrechten Mittelparallele des Rechteckes.

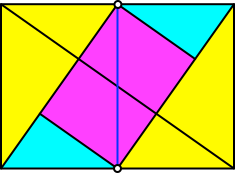
Abb. 5: Labiles Gleichgewicht des magenta Rechtecks

Die Lote auf die Diagonale teilen diese in drei gleiche Teile (Abb. 6).

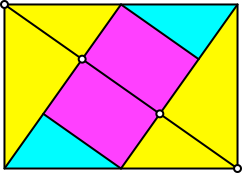
Abb. 6: Dritteln der Diagonale

Auch die Diagonalenlote werden in drei gleiche Teile zerlegt (Abb. 7).

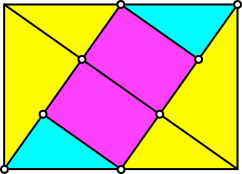
Abb. 7: Dritteln der Diagonalenlote

Dieses Dritteln der Diagonale und der Diagonalenlote kann mit einer Triangulation mit kongruenten Dreiecken illustriert werden (Abb. 8).

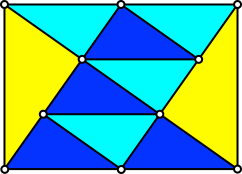
Abb. 8: Rasterung

Da das zentrale magenta Rechteck ebenfalls das DIN-Format hat, kann es durch eine passend verkleinerte und verdrehte Kopie der Ausgangsfigur ersetzt werden (Abb. 9). Iteration dieses Vorganges führt auf eine eckige logarithmische Spirale.

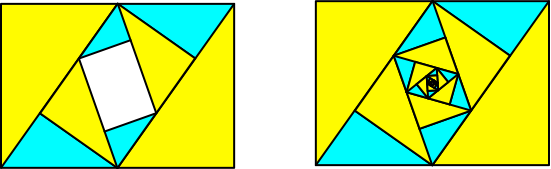
Abb. 9: Spirale

4.3 Quadrat im Rechteck

Interessant ist die Station wo das magenta Rechteck ein Quadrat ist (Abb. 10).

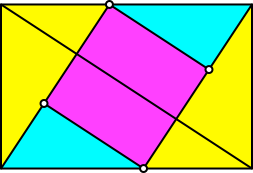
Abb. 10: Quadrat im Rechteck

Bei der Höhe 1 des Rechtecks hat es die Länge t, welche die reelle Lösung der kubischen Gleichung

ist. Die Rechnung ergibt:

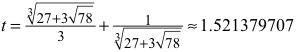
Diese Situation ist nicht mit Zirkel und Lineal konstruierbar.

4.4 Goldener Schnitt

Die nächste Station ist der Goldene Schnitt (Abb. 11), also das Rechteck mit dem Seitenverhältnis:

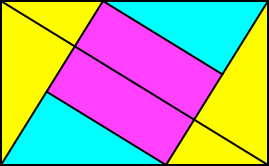
Abb. 11: Goldenes Rechteck

Wir können einen Zick-Zack-Weg einbauen (rot in Abb. 12). Er besteht aus drei gleich langen Strecken, welche orthogonal aufeinanderfolgen.

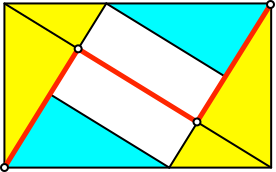
Abb. 12: Zick-Zack-Weg

Die Situation kann auch mit Quadraten illustriert werden (Abb. 13).

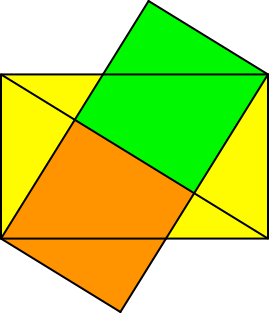
Abb. 13: Quadrate

4.5 Wurzel aus drei

Beim Seitenverhältnis √3 :1 haben die rechtwinkligen Dreiecke die spitzen Winkel 30° und 60° (Abb. 14). Es sind halbe gleichseitige Dreiecke.

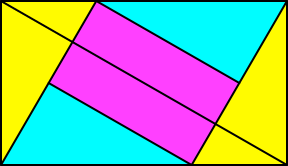
Abb. 14: Halbe gleichseitige Dreiecke

Die linke und die rechte Ecke des magenta Rechteckes liegen auf gleicher Höhe (Abb. 15), und zwar auf der waagerechten Mittelparallele des Rechteckes.

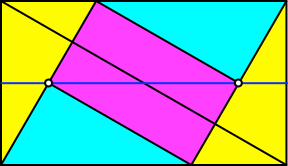
Abb. 15: Ecken auf gleicher Höhe

Das magenta Rechteck hat ebenfalls das Seitenverhältnis √3 : 1. Es kann daher durch eine passend verkleinerte und verdrehte Kopie des Ausgangsrechteckes ersetzt werden (Abb. 16). Iteration führt auf eine eckige logarithmische Spirale. Man beachte den Unterschied zur Abbildung 9.

Abb. 16: Spirale

Die Diagonale wird durch die Diagonalenlote geviertelt (Abb. 17).

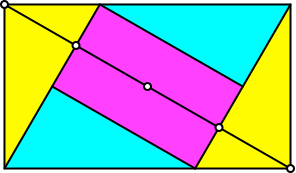
Abb. 17: Vierteln der Diagonale

Auch die Diagonalenlote werden geviertelt (Abb. 18).

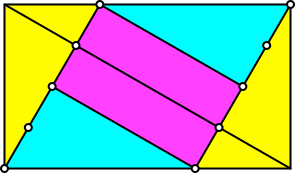
Abb. 18: Vierteln der Diagonalenlote

Dieses Vierteln der Diagonale und der Diagonalenlote kann mit einer Triangulation mit kongruenten Dreiecken illustriert werden (Abb. 19).

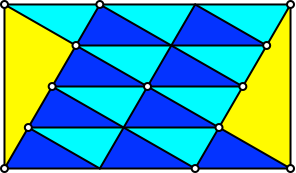
Abb. 19: Triangulation

Das Rechteck kann in sechs kongruente rechtwinklige Dreiecke zerlegt werden (Abb. 20).

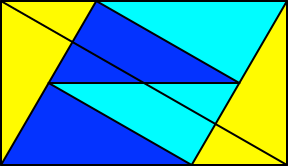
Abb. 20: Sechs kongruente Dreiecke

Wir können auch gleichseitige Dreiecke einbauen (Abb. 21 und 22).

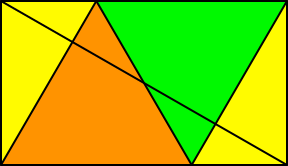
Abb. 21: Gleichseitige Dreiecke

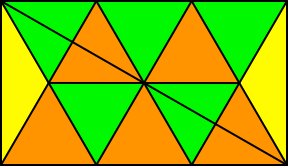
Abb. 22: Kleine gleichseitige Dreiecke

Weblinks

Hans Walser: Quadrat im Rechteck

http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadrat_im_Rechteck/Quadrat_im_Rechteck.html

Literatur

Walser, Hans (2021): Spiralen in Rechtecken. MI, Mathematikinformation Nr. 75, 15. September 2021. ISSN 1612-9156. 3-15.

Walser, Hans (2022): Spiralen, Schraubenlinien und spiralartige Figuren. Mathematische Spielereien in zwei und drei Dimensionen. Springer Spektrum. ISBN 978-3-662-65131-5 und ISBN 978-3-662-65132-2 (eBook).