1 Worum geht es?

Ein gleichschenkliges Trapez im Kontext des DIN-Formates.

2 Das DIN-Trapez

Das DIN-Trapez entsteht folgendermaßen. Wir falten ein Papier im DIN-Format, zum Beispiel DIN A4, längs einer Diagonale und nehmen die konvexe Hülle der Figur (Abb. 1).

Abb. 1: DIN-Trapez

Im DIN-Trapez schneiden sich die Diagonalen mit dem Winkel ω = arccos(1/3) ≈ 70.529° (Abb. 2). Die ist ebenfalls der Schnittwinkel der Diagonalen in einem DIN-Rechteck. Weiter ist es auch der Winkel, unter dem sich die Raumdiagonalen des Würfels schneiden sowie der Winkel zwischen zwei benachbarten Seitenflächen des Tetraeders (Diederwinkel des Tetraeders). Sein Ergänzungswinkel 180° – ω ≈ 109.471° ist der Diederwinkel des Oktaeders. Diese beiden Winkel spielen in der Kristallografie eine wichtige Rolle.

Die lange Parallelseite des DIN-Trapezes hat die Länge √3, die kurze ein Drittel davon, also 1/√3.

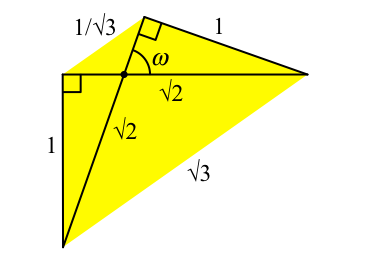
Abb. 2: Diagonalenschnittwinkel

3 Alternativer Zugang

Wir zeichnen einen Raster aus 2 × 3 = 6 kongruenten DIN-Rechtecken (Abb. 3) und schneiden links und rechts oben eine Ecke ab.

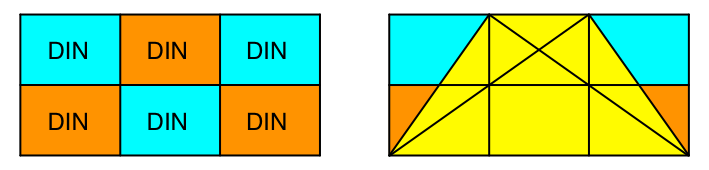
Abb. 3: Konstruktion im DIN-Raster

4 In der Lemniskate

Das DIN-Trapez können wir in die Lemniskate einbetten (Abb. 4). Der Mittelpunkt der einen Diagonalen ist im Doppelpunkt der Lemniskate, der Mittelpunkt der anderen Diagonalen liegt auf der Lemniskate.

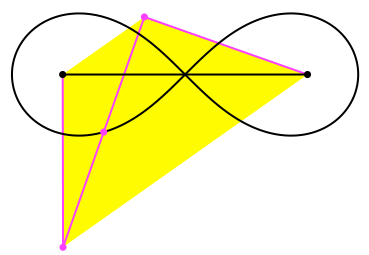
Abb. 4: DIN-Trapez und Lemniskate

Die Tangente im so konstruierten Punkt der Lemniskate verläuft durch einen der beiden schwarzen Verankerungspunkte (Abb. 5). Mit DGS erhärtet.

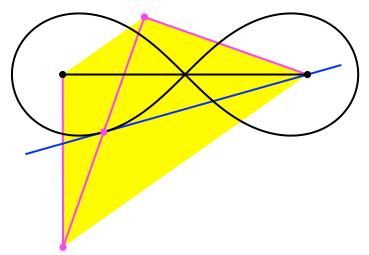
Abb. 5: Tangente

5 Im Würfel

Wir unterteilen die Kanten eines Würfels je in drei Teile und entsprechend den Würfel in 3³ = 27 Teilwürfel. Wir arbeiten nun weiter mit dem Gesamtwürfel und dem Teilwürfel in der Mitte (Abb. 6).

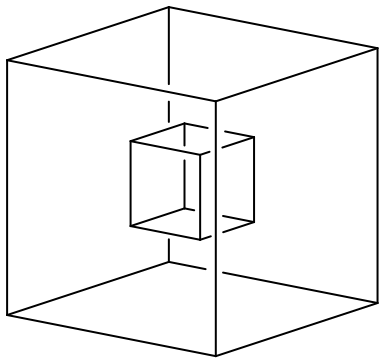
Abb. 6: Würfel und Teilwürfel in der Mitte

In diese Figur können wir DIN-Trapeze einpassen (Abb. 7). Nachweis durch Rechnung oder durch Überlegung.

Abb. 7: DIN-Trapez

Insgesamt lassen sich zwölf solche DIN-Trapeze einpassen, für jede Würfelkante eines (Abb. 8 und 9). Wir haben also ein Kantenmodell des Würfels.

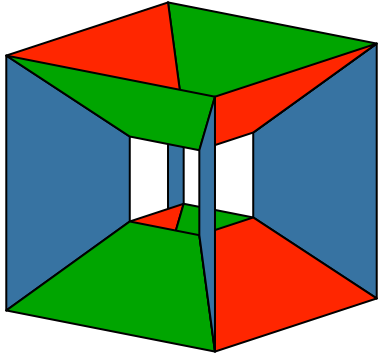
Abb. 8: Zwölf DIN-Trapeze

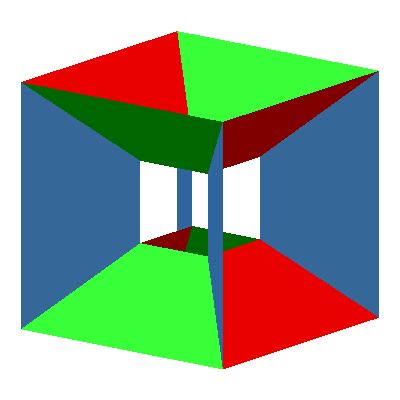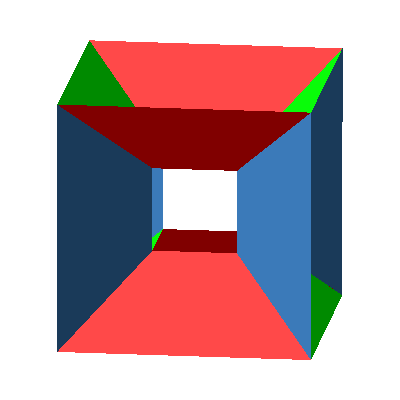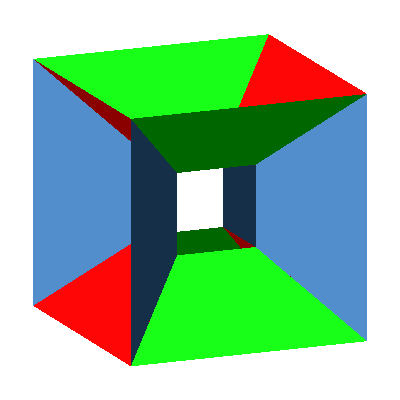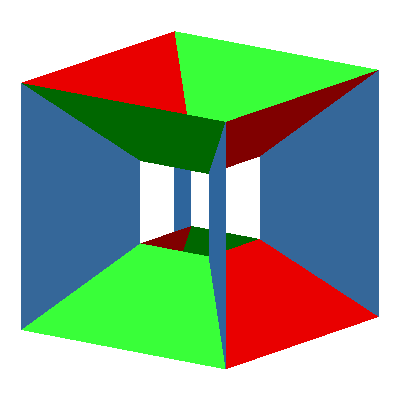
Abb. 9: Kantenmodell des Würfels

Weblinks

Hans Walser: Lemniskate

http://www.walser-h-m.ch/hans/Miniaturen/L/Lemniskate5/Lemniskate5.html

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.