Hans Walser, [20191021]
1 2 3
1 Worum geht es?
Spiel mit Zahlen.
2 Problemstellung
Es ist:
1 + 2 + 3 = 1 × 2 × 3 (1)
Gibt es weitere drei aufeinanderfolgende Zahlen mit der entsprechenden Eigenschaft?
3 Bearbeitung
Wir nennen die drei Zahlen z, z + 1, z + 2. Daraus ergibt sich die Bedingung:
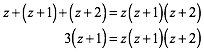 (2)
(2)
Die erste
Lsung (Faktor ![]() ) dieser kubischen Gleichung ist
) dieser kubischen Gleichung ist ![]() . Daraus ergeben sich die drei Zahlen –1, 0, +1.
. Daraus ergeben sich die drei Zahlen –1, 0, +1.
Division
durch ![]() fhrt auf
die quadratische Gleichung
fhrt auf
die quadratische Gleichung
![]() (3)
(3)
Dies
ergibt die beiden Lsungen ![]() und
und ![]() . Die zugehrigen Lsungstripel sind 1, 2, 3 und
–3, –2, –1.
. Die zugehrigen Lsungstripel sind 1, 2, 3 und
–3, –2, –1.
Wenn wir die Lsungstripel als kartesische Koordinaten deuten, erhalten wir drei kollineare quidistante Punkte (Abb. 1). Der Abstand von Punkt zu Punkt:
![]() (4)
(4)
Der Richtungsvektor der Geraden ist:
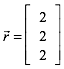 (5)
(5)
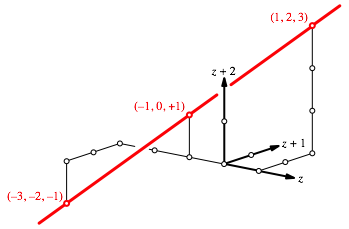
Abb. 1: Kollineare quidistante Punkte
4 Verallgemeinerung
Wir fragen nach n aufeinanderfolgenden Zahlen mit der zu (1) analogen Bedingung:
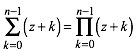 (6)
(6)
4.1 Zwei Zahlen
Wir haben die Bedingung:
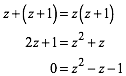 (7)
(7)
Die Lsungen sind der goldene Schnitt (Walser 2013). Mit
![]() (8)
(8)
erhalten wir die Zahlenpaare
![]() und
und ![]() (9)
(9)
oder umgeformt:
![]() und
und ![]() (10)
(10)
Die nach (6) zugehrigen Summen beziehungsweise Produkte sind:
![]() und
und ![]() (11)
(11)
Wir haben keine ganzzahlige, sondern irrationale Lsungen.
4.2 Vier Zahlen
Fr vier Zahlen liefert die Bedingung (6) bezglich z die beiden nicht ganzzahligen Lsungen:
![]() (12)
(12)
4.3 Fnf Zahlen
Fr fnf Zahlen liefert die Bedingung (6) bezglich z die folgenden fnf Lsungen:
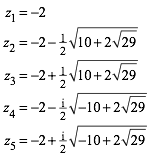 (13)
(13)
4.4 19 Zahlen
Fr 19 Zahlen erhalten wir folgende numerischen Lsungen bezglich z:
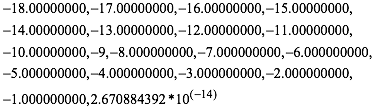 (14)
(14)
Wir haben eine ganzzahlige Lsung, nmlich 9. Die brigen Lsungen sind offenbar nur nherungsweise ganzzahlig.
4.5 Vermutung
Fr eine ungerade Anzahl u = 2m + 1, u > 3, von Zahlen haben wir die Zahl –m als ganzzahlige Lsung bezglich z. Die brigen Lsungen sind nicht ganzzahlig, nhern sich aber fr gro§e u ganzen Zahlen an. Fr eine gerade Anzahl g von Zahlen haben wir keine ganzzahlige Lsung. Fr gro§e g nhern sich die Lsungen aber ganzen Zahlen an.
Wir haben
somit ein Parittsproblem.
Diese Vermutung wird in einer folgenden Studie untersucht.
Literatur
Walser, H. (2013): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
Websites
Lehrer Lmpel: 1 2 3
http://www.walser-h-m.ch/hans/Miniaturen/1/1_2_3/1_2_3.htm