Hans Walser
Umkehrung
Arbeitskreis Geometrie der GDM
SaarbrŸcken, 14. – 16. September 2018
Zusammenfassung: Die Umkehrung einer klassischen Schulaufgabe (Sekundarstufe) fŸhrt zu einer Verallgemeinerung der Begriffe ãThaleskreisÒ und ãOrtsbogenÒ.
1 Wie das Problem entstand
Eine
klassische Aufgabe im Abiturtraining geht so (vgl. etwa Weber und Zillmer 2002,
S. 66, Aufg. DA 32): Gegeben sind ein Punkt 
und eine Parabel 
.
Gesucht sind die Tangenten von diesem Punkt an die Parabel sowie der eingeschlossene
Winkel.
Nun kann man die Frage umkehren: Wir geben nicht den Punkt P sondern den Schnittwinkel vor und suchen nach den passenden Punkten P.
ZunŠchst lšsen wir die Schulaufgabe.
Es gibt zwei Herangehensweisen:
Erster Lšsungsweg: Wir nehmen alle Geraden durch den Punkt P und wŠhlen dann diejenigen aus, welche die Parabel p berŸhren. Dieser Lšsungsweg benštigt nur Kenntnisse der quadratischen Gleichung (10. Schuljahr)
Zweiter Lšsungsweg: Wir nehmen alle Tangenten an die Parabel p und wŠhlen diejenigen aus, welche durch den Punkt P verlaufen. Dieser Lšsungsweg benštigt auch Differentialrechnung (11. Schuljahr).
2 Gibt es einen geometrischen Lšsungsweg?
Den gibt es, und er ist verfahrensmŠ§ig sehr einfach. Er geht im Prinzip fŸr alle Kegelschnitte.
2.1 Parabel
Wir arbeiten mit dem Brennpunkt F und der Leitlinie l der Parabel p (Abb. 1a).
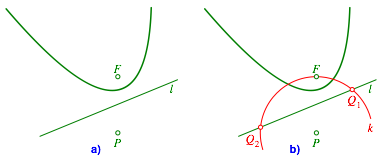
Abb. 1: Parabel. Erster Schritt
Wir schneiden den Kreis k um P durch F und mit der Leitlinie l in Q1 und Q2 (Abb. 1b).
Die Mittelsenkrechten der Strecken FQ1 und FQ2 sind die gesuchten Tangenten t1 beziehungsweise t2 (Abb. 2a).
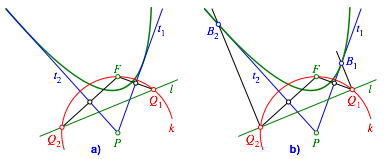
Abb. 2: Parabeltangenten
Die BerŸhrungspunkte liegen auf den Loten zur Leitlinie l durch Q1 und Q2 (Abb. 2b).
Diese Konstruktion folgt aus der Abstandsdefinition und der Reflexionseigenschaft der Parabel.
2.2 Ellipse
Die Tangentenkonstruktion fŸr die Ellipse geht im Prinzip analog. Von einer Ellipse e seien die beiden Brennpunkte F1 und F2 sowie die LŠnge 2a der langen Achse bekannt (Abb. 3a).
Abb. 3: Ellipse
Als ersten Schritt zeichnen wir einen Kreis l mit dem Zentrum F2 und dem Radius 2a (dieser Kreis entspricht der Leitlinie der Parabel) sowie einen Kreis k um P durch den anderen Brennpunkt F1. Die Schnittpunkte der beiden Kreise bezeichnen wir mit Q1 und Q2 (Abb. 3b).
Die Mittelsenkrechten der Strecken F1Q1 und F1Q2 sind die gesuchten Tangenten t1 beziehungsweise t2 (Abb. 4a). Die BerŸhrungspunkte liegen auf den Strecken F2Q1 und F2Q2 (Abb. 4b).
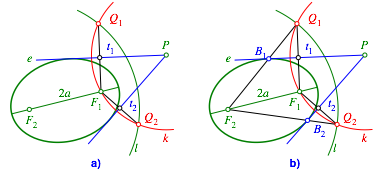
Abb. 4: Ellipsentangenten
Bemerkung 1: Die Konstruktion ist asymmetrisch, indem die beiden Brennpunkte unterschiedlich verwendet werden.
Bemerkung 2: Die in der Schule Ÿbliche Konstruktion der Ellipsentangente benutzt die AffinitŠt. Die Ellipse wird affin zu einem Kreis aufgeblasen, dabei wird der Punkt P mitgenommen. Dann werden die Kreistangenten gezeichnet und anschlie§end das Ganze rŸckwŠrts abgebildet. Diese Konstruktion ist nicht auf die Hyperbel Ÿbertragbar.
Bemerkung 3: Wenn der Brennpunkt F2 (nach links) ins Unendliche abrauscht ergibt sich aus der Abbildung 4 die Situation der Parabel.
Bemerkung 4: Wenn wir die beiden Brennpunkte F1 und F2 zusammenfallen lassen, ergibt sich eine einfache Tangentenkonstruktion an den Kreis, welche ohne den Thaleskreis auskommt.
Bemerkung 5: Die Konstruktion fŸr die Hyperbel geht všllig analog zur Ellipse.
3 Umkehrung
Von welchen Punkten aus sehen wir die Parabel unter einem vorgegebenen Winkel?
3.1 Gibt es Šhnliche Fragen?
Von welchen Punkten aus sehen wir eine Strecke unter einem vorgegebenen Winkel? Die Lšsung ist das Ortsbogenpaar, im Sonderfall des rechten Winkels der Thaleskreis.
Wir kšnnen die Strecke durch ein Polygon ersetzen: von welchen Punkten aus sehen wir das regelmŠ§ige Siebeneck (Abb. 5a) unter einem Winkel von 60¡? Die Lšsung ist der Au§enrand der Kreisfiguration der Abbildung 5b. Die Kreise sind Ortsbogen fŸr den Winkel 60¡ Ÿber den Diagonalen des Siebenecks.
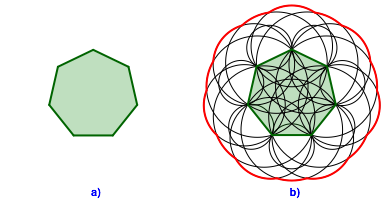
Abb. 5: RegelmŠ§iges Siebeneck gesehen unter 60¡
Wir werden im Folgenden die Parabel auf Kegelschnitte verallgemeinern: von welchen Punkten aus sehen einen Kegelschnitt unter einem vorgegebenen Winkel? ZunŠchst untersuchen wir die Situation fŸr rechte Winkel (Thalesproblem).
4 Rechte Winkel als Sehwinkel
Von welchen Punkten aus sehen wir einen Kegelschnitt unter einem rechten Winkel?
4.1 Parabel
Die Thaleskurve ist die Leitlinie der Parabel (Abb. 6). Der Beweis ist eine schšne †bung in Parabelgeometrie.
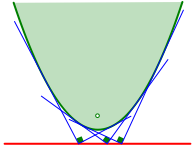
Abb. 6: Parabel und Leitlinie als Thaleskurve
4.2 Ellipse
Wir erhalten interessanterweise einen Kreis (Abb. 7). Die Thaleskurve einer Ellipse ist also ein Kreis. Der Beweis ist recht happig.
Die Ecken der ãUmrechteckeÒ einer Ellipse liegen auf einem Kreis.
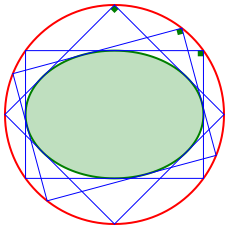
Abb. 7: Ellipse und Thaleskreis
4.3 Hyperbel
Die
Thaleskurve existiert nur fŸr 
und ist
ebenfalls ein Kreis.
5 Beliebige Winkel als Sehwinkel
Gesucht
sind die Punkte, von denen aus ein gegebener Kegelschnitt unter einem vorgegebenen
Winkel 
gesehen
wird.
5.1 Parabel
Die gesuchten Punkte liegen auf einem Hyperbelast (Abb. 8).
Auf dem
zweiten Hyperbelast (magenta in Abb. 8) liegen die Punkte, von denen aus die
Parabel unter dem Winkel 
gesehen
wird. Einer der beiden Brennpunkte der Hyperbel ist auch Brennpunkt der
Parabel.
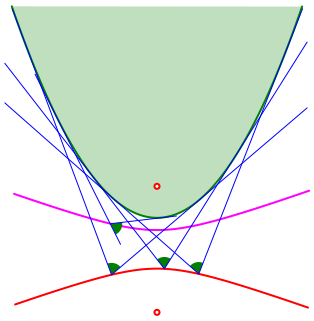
Abb. 8: Parabel und Hyperbelast
Die
Abbildung 9 zeigt die Hyperbelschar fŸr Sehwinkel 
. Die Kurven sind eine Art Niveaulinien fŸr 
. Die Hyperbeln haben einen Brennpunkt gemeinsam, dies
ist auch der Brennpunkt der Parabel.
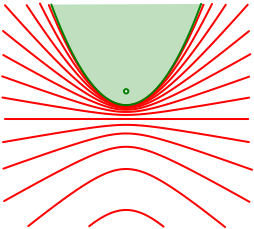
Abb. 9: Hyperbelschar
5.2 Ellipse
Die Abbildung 10 zeigt zwei Beispiele.
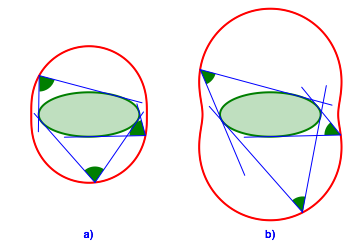
Abb. 10: Ellipse
Die gesuchte Punktmenge ist kein Kegelschnitt mehr. Analoges gilt fŸr die Hyperbel.
Dank
Der Autor dankt Kolleginnen und Kollegen des Liechtensteinischen Gymnasiums Vaduz fŸr Anregungen und Hinweise.
Websites
[1] Hans Walser: Sehwinkel bei Kegelschnitten (abgerufen 15.06.2018):
www.walser-h-m.ch/hans/Miniaturen/S/Sehwinkel_Kegelschnitte/Sehwinkel_Kegelschnitte.htm
[2] Hans Walser: Tangente an Kegelschnitt (abgerufen 03.06.2018):
www.walser-h-m.ch/hans/Miniaturen/T/Tangente_an_Kegelschnitt/Tangente_an_Kegelschnitt.htm
[3] Hans Walser: Thaleskreis an Ellipse und Hyperbel (abgerufen 15.06.2018):
www.walser-h-m.ch/hans/Miniaturen/T/Thaleskreis_E_H/Thaleskreis_E_H.htm
[4] Hans Walser: Kreistangente ohne Thaleskreis (abgerufen 18.06.2018):
www.walser-h-m.ch/hans/Miniaturen/K/Kreistangente_o_Tk/Kreistangente_o_Tk.htm
Literatur
Weber, Karlheinz und Zillmer, Wolfgang (2002): Mathematik Gymnasiale Oberstufe. Grundkurs Aufgabenbuch. Analysis, Analytische Geometrie und Lineare Algebra. Stochastik. Berlin – Frankfurt M: Duden Paetec Schulbuchverlag. ISBN 3-89818-110-3.