Hans Walser
Rechtwinkliges Dreieck und Binomialverteilung
1 Worum geht es?
Durch iterierte Zerlegung eines rechtwinkligen Dreiecks durch die Hhe kommen wir zu den Binomialkoeffizienten und der Binomialverteilung.
Die berlegungen knnen mit Schere und Papier nachvollzogen werden.
2 Mit Geodreieck und Schere
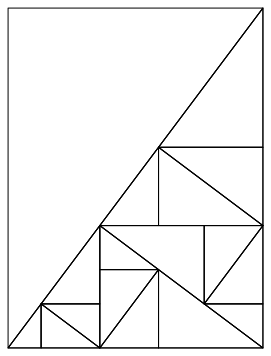
Abb. 0: Arbeitsvorlage
Wir arbeiten entweder mit dem wei§en Dreieck links oben (oder mit einem beliebigen anderen rechtwinkligen Dreieck), zeichnen mit dem Geodreieck die Hhe und schneiden aus. In den beiden Teildreiecken zeichnen wir wieder je die Hhe und zerlegen mit der Schere. Und so weiter und so fort.
Alternativ knnen wir im schon prparierten rechtwinkligen Dreieck rechts unten mit den Hhen zerlegen, die Teildreiecke der Gr§e nach ordnen und am Schluss versuchen, die Teildreiecke wieder zum gro§en rechtwinkligen Dreieck zusammenzufgen.
Alternativ knnen wir im schon prparierten rechtwinkligen Dreieck rechts unten die Dreiecke der Gr§e nach ausmalen und dann die Farben auszhlen.
Die Arbeitsvorlage kann in [1] als pdf heruntergeladen werden.
3 Zerlegungen des rechtwinkligen Dreiecks
Ein Dreieck wird durch eine Ecktransversale in zwei Teildreiecke zerlegt (Hlzl 2017). Dabei knnen verschiedene Bedingungen an das Startdreieck und die beiden Teildreiecke gestellt werden.
Wir besprechen den Sonderfall eines rechtwinkligen Dreiecks, welches wir durch die Hhe in zwei Teildreiecke zerlegen. Die beiden Teildreiecke sind wieder rechtwinklig.
Dabei iterieren wir den Zerlegungsprozess.
Die Abbildung 1 zeigt das Startdreieck. Da wir noch nichts zerlegt haben, bleibt vorerst einmal dieses Startdreieck.

Abb. 1: Startdreieck
Erster Schritt: wir zerlegen mit der zur Hypotenuse senkrecht stehenden Hhe. Es entstehen zwei ungleich gro§e Teildreiecke (Abb. 2).

Abb. 2: Zerlegung durch die Hhe
Zweiter Schritt: Und nun kommt das Entscheidende. Wir zerlegen auch jedes der beiden Teildreiecke mit seiner Hypotenusenhhe (Abb. 3).

Abb. 3: Zweite Zerlegung durch die Hhe
Das gibt zunchst vier Teildreiecke. Dabei ist aus Symmetriegrnden sofort klar, dass die beiden mittleren gleich gro§ sind. Das eine der beiden mittleren Dreiecke ist dabei das gro§e Teildreieck vom vorhergehenden kleinen Teildreieck, und das andere das kleine Teildreieck vom vorhergehenden gro§en Teildreieck.
Die Anzahlen 1, 2, 1 erinnern an die Binomialkoeffizienten.
Die Abbildungen 4 und 5 zeigen die beiden weiteren Zerlegungen.

Abb. 4: Dritte Zerlegung
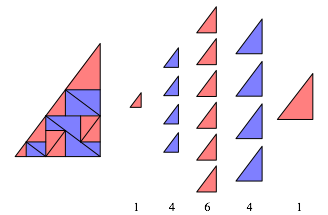
Abb. 5: Vierte Zerlegung
4 Binomialkoeffizienten
Die jeweiligen Anzahlen der Teildreiecke sind vermutlich die Binomialkoeffizienten (Abb. 6).

Abb. 6: Binomialkoeffizienten
Um dies exemplarisch einzusehen, vermischen wir die figrlichen Aufzhlungen der Abbildungen 3 und 4. Die in der Abbildung 7 wei§ unterlegten Teile entstammen der Abbildung 3, die gelb unterlegten der Abbildung 4.
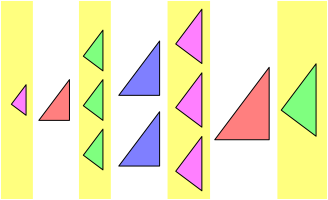
Abb. 7: Vermischung
Nun zerlegen wir die Dreiecke aus der Abbildung 3, also die in der Abbildung 7 wei§ unterlegten Dreiecke, durch ihre Hypotenusenhhen (Abb. 8).
Wir knnen die Teildreiecke nun eins zu eins (bijektiv) den gelb unterlegten Dreiecken zuordnen.
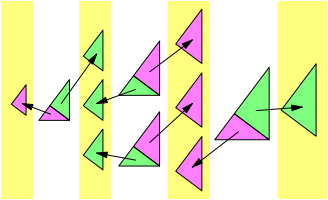
Abb. 8: Zerlegung und Zuordnung
Im Zahlendreieck der Binomialkoeffizienten haben wir damit die Zuordnung der Abbildung 9 vorgenommen.

Abb. 9: Im Zahlendreieck
Damit ergibt sich allgemein die fr die Binomialkoeffizienten relevante Rekursion:
![]() (1)
(1)
5 Didaktische Zwischenbemerkung
Die Zerlegungen knnen mit Schere und Papier nachvollzogen werden. So erhalten wir einen modellm§igen Zugang zu den Binomialkoeffizienten.
Neckisch ist auch das Puzzle, die einzelnen Teildreiecke ohne Schnittvorlage wieder zum Startdreieck zusammenzufgen.
6 Ma§verhltnisse
Fr die Berechnungen im rechtwinkligen Dreieck verwenden wir die blichen Bezeichnungen a und b fr die beiden Katheten und c fr die Hypotenuse. Fr die Dreiecke der Abbildung 2 erhalten wir damit die in der Abbildung 10 rot angegebenen hnlichkeitsfaktoren (Lngenma§stbe oder Lngenvernderungsfaktoren). Die Flchenma§stbe sind die Quadrate davon (blau in Abb. 10).
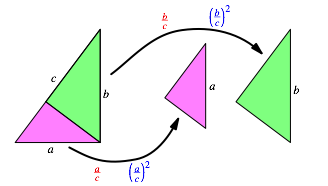
Abb. 10: Lngenma§stbe (rot) und Flchenma§stbe (blau)
7 Relative Hypotenusenabschnitte
Fr das Ausgangsdreieck definieren wir die relativen Hypotenusenabschnitte:
![]() (2)
(2)
Um daraus die in der Schule blichen vom Hhenfu§punkt ausgehenden absoluten Hypotenusenabschnitte zu erhalten, muss man noch mit der Hypotenusenlnge c multiplizieren.
Diese relativen Hypotenusenabschnitte sind auch die Flchenma§stbe bei der Zerlegung durch die Hypotenusenhhe gem§ Abbildung 10.
Weiter gilt nach dem Satz des Pythagoras:
![]() (3)
(3)
Die beiden Variablen p und q sind also auch passend fr berlegungen mit Wahrscheinlichkeit und Gegenwahrscheinlichkeit.
8 Flchenanteile
Wir knnen nun mit den Variablen p und q die Flchenanteile der Teildreiecke der Abbildungen 2 bis 5 am Startdreieck angeben (Abb. 11-14).

Abb. 11: Flchenanteile bei einmaligem Zerlegen

Abb. 12: Flchenanteile bei zweimaligem Zerlegen

Abb. 13: Flchenanteile bei dreimaligem Zerlegen
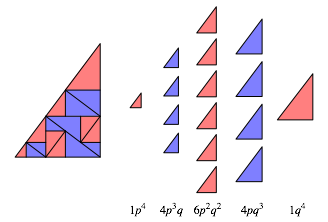
Abb. 14: Flchenanteile bei viermaligem Zerlegen
Wir
erkennen die Binomialverteilung in folgender Form: in der n-ten Zerlegung ist der Flchenanteil aller ![]() gleich
gro§er Teildreiecke:
gleich
gro§er Teildreiecke:
![]() (4)
(4)
9 Und wo bleibt der Baum?
In der Schule ist es blich, im Kontext der Binomialverteilung mit einem Baumgerst etwa gem§ der Abbildung 15 zu arbeiten.
Dieser Baum visualisiert die kombinatorischen Anzahlen mit den Binomialkoeffizienten, er ist aber keine Visualisierung der Ma§verhltnisse mit der Binomialverteilung.
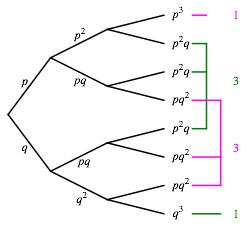
Abb. 15: Kombinatorischer Baum
10 Der Pythagorasbaum
Um die kombinatorischen Anzahlen zusammen mit den Ma§verhltnissen zu visualisieren, verfahren wir wie folgt (Abb. 16-21).

Abb. 16: Am Anfang war das Quadrat

Abb. 17: Gru§ von Pythagoras
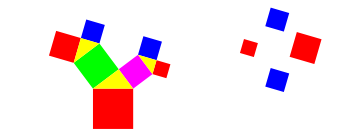
Abb. 18: Zweiter Gru§ von Pythagoras
Wir sehen, dass die Quadrate der jeweils neuen Runde gleich orientiert sind.
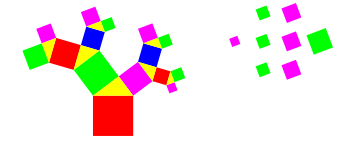
Abb. 19: Dritte Verstelung
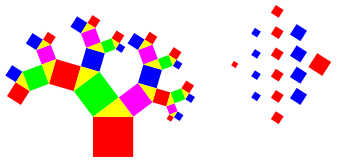
Abb. 20: Vierte Verstelung
Die Weiterfhrung ad infinitum fhrt zu einem Fraktal (Abb. 21). Hat das etwas mit der Normalverteilung zu tun?

Abb. 21: Pythagorasbaum
Literatur
Gltzner, Fabian (2017): Binomialverteilung erkunden. Beispiele untersuchen, systematisieren und erweitern. mathematik lehren 201 | 2017, 36-41.
Hlzl, Reinhard (2017): Dreiecke in Dreiecke zerlegen. Welche Eigenschaften und Zusammenhnge findest du? mathematik lehren 201 | 2017, 12-15.
Walser, Hans (2017): Dreiecksunterteilung und Binomialverteilung – In: Fachnewsletter mathematik lehren vom 18.9.2017
Walser, Hans (2017): Rechtwinklige Dreiecke ... . Ideenkiste. ml, mathematik lehren 204 | 2017, 51.
Websites
[1] Hans Walser: Arbeitsvorlage (10.12.2017):
http://www.walser-h-m.ch/hans/Vortraege/20180306/Puzzle_24_bw.pdf