Hans Walser, [20180925]
Zwei Folgen
1 Worum geht es?
Zwei gekoppelte Folgen von Rechtecken und zugehrige Zahlenfolgen.
Variante von [1].
2 Flchengleiche Rechtecke anfgen
Die Abbildung 1 zeigt die Entstehung einer Doppelfolge von flchengleichen Rechtecken. Die beiden ersten Rechtecke sind Quadrate.
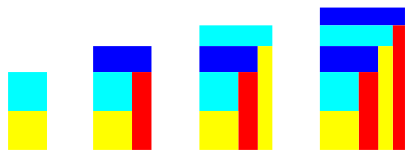
Abb. 1: Folgen flchengleicher Rechtecke
Die Abbildung 2 zeigt ein ausfhrlicheres Beispiel.
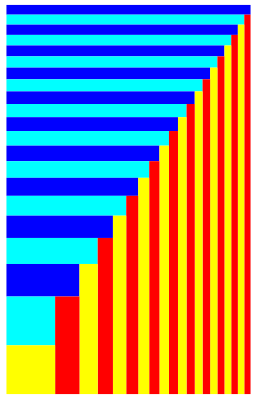
Abb. 2: Ausfhrliches Beispiel
3 Zahlenfolgen
Der Figur ordnen wir zwei Zahlenfolgen xn und yn zu gem§ Abbildung 3. Dabei verwenden wir die Startwerte:
![]() (1)
(1)
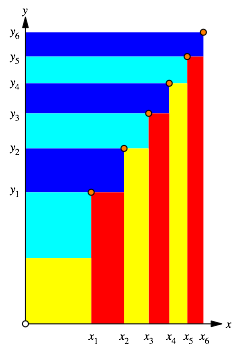
Abb. 3: Zahlenfolgen
Aus der Bedingung der Flchengleichheit (alle Rechtecke haben den Flcheninhalt 1) folgt:
![]() (2)
(2)
Analog:
![]() (3)
(3)
Man beachte die Asymmetrie der Indizes zwischen (2) und (3).
Die
zusammengesetzten Rechtecke mit der linken unteren Ecke im Ursprung ![]() und der rechten
oberen Ecke im Punkt mit den Koordinaten
und der rechten
oberen Ecke im Punkt mit den Koordinaten ![]() enthalten
2n Rechtecke mit dem Flcheninhalt 1
und haben somit den Flcheninhalt 2n.
Daher ist:
enthalten
2n Rechtecke mit dem Flcheninhalt 1
und haben somit den Flcheninhalt 2n.
Daher ist:
![]() (4)
(4)
Damit knnen wir yn in (2) eliminieren und erhalten die Rekursion:
![]() (5)
(5)
Mit dem Startwert x1 = 1 ergibt sich:
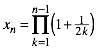 (6)
(6)
Die Tabelle 1 gibt die ersten Werte, wie sie aus dem Computer kommen.
|
n |
|
|
1 |
1 |
|
2 |
|
|
3 |
|
|
4 |
|
|
5 |
|
|
6 |
|
Tab. 1: Werte
4 Analyse der Zahlenfolge
Leider wird man in der Schule angehalten, Brche vollstndig zu krzen. Dies ist nicht immer sinnvoll. Die Tabelle 2 enthlt dieselben Werte wie die Tabelle 1, aber in zustzlichen Spalten teilweise weniger gekrzt und faktorisiert.
|
n |
|
|
|
|
1 |
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
5 |
|
|
|
|
6 |
|
|
|
Tab. 2: Werte in anderer Schreibweise
Wir stellen Regelm§igkeiten fest.
In der
zweiten Wertspalte sind die Zhler bei den Brchen die natrlichen Zahlen n und die Nenner die geometrische Folge ![]() .
.
In der
dritten Wertspalte sind die Zhler die ungeraden Zahlen 2n – 1 und die Nenner die geometrische Folge ![]() .
.
Und was
hat der Zahlenerkennungsdienst zur Zahlenfolge ![]() , 1, 3, 10, 35, 126, 462, ... zu sagen? Diese Zahlen erscheinen
in beiden Spalten als Faktoren, allerdings versetzt.
, 1, 3, 10, 35, 126, 462, ... zu sagen? Diese Zahlen erscheinen
in beiden Spalten als Faktoren, allerdings versetzt.
Diese
Zahlen, zunchst ohne das fhrende ![]() , erscheinen auch im Pascalschen Dreieck der
Binomialkoeffizienten (grn unterlegt in Abb. 4).
, erscheinen auch im Pascalschen Dreieck der
Binomialkoeffizienten (grn unterlegt in Abb. 4).
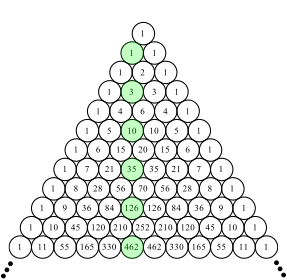
Abb. 4: Binomialkoeffizienten
Somit erhalten wir zwei weitere Darstellungen der Folge xn:
![]() (7)
(7)
Und:
![]() (8)
(8)
Die unterschiedliche Indizierung der Binomialkoeffizienten zwischen (7) und (8) rhrt von der versetzten Position in der Tabelle 2 her.
Die
Formel (8) funktioniert fr n = 1 zunchst
nicht. Wir erhalten den Binomialkoeffizienten ![]() . Um das doch hinzubringen, erweitern wir das
Pascalsche Dreieck der Binomialkoeffizienten gem§ Abbildung 5. In den wei§en
Feldern stehen Nullen. Man beachte, dass die bliche Rekursionsformel fr die
Binomialkoeffizienten immer noch spielt.
. Um das doch hinzubringen, erweitern wir das
Pascalsche Dreieck der Binomialkoeffizienten gem§ Abbildung 5. In den wei§en
Feldern stehen Nullen. Man beachte, dass die bliche Rekursionsformel fr die
Binomialkoeffizienten immer noch spielt.
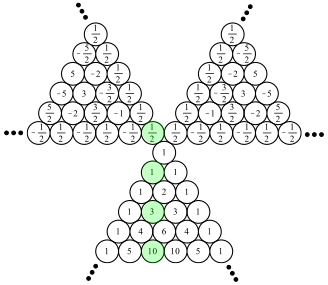
Abb. 5: Binomialkoeffizienten erweitert
Dir Formeln (7) und (8) knnen mit (5) und der Tabelle 2 induktiv bewiesen werden.
5 Grenzform
Die
Abbildungen (1) und (2) lassen vermuten, dass die zusammengesetzten Rechtecke
mit der linken unteren Ecke im Ursprung ![]() und der
rechten oberen Ecke im Punkt mit den Koordinaten
und der
rechten oberen Ecke im Punkt mit den Koordinaten ![]() sich einem
Rechteck mit konstantem Seitenverhltnis annhert, dass also
sich einem
Rechteck mit konstantem Seitenverhltnis annhert, dass also ![]() konvergiert.
konvergiert.
Wegen (4) ist:
![]() (9)
(9)
Weiter vermuten wir, dass die zusammengesetzten
Rechtecke mit der linken unteren Ecke im Ursprung ![]() und der
rechten oberen Ecke im Punkt mit den Koordinaten
und der
rechten oberen Ecke im Punkt mit den Koordinaten ![]() sich einem
Rechteck mit demselben konstantem Seitenverhltnis annhert, dass also
sich einem
Rechteck mit demselben konstantem Seitenverhltnis annhert, dass also ![]() konvergiert und denselben Grenzwert hat.
Wegen (4) ist:
konvergiert und denselben Grenzwert hat.
Wegen (4) ist:
![]() (10)
(10)
Die Tabelle 3 zeigt einige numerische Werte.
|
n |
|
|
|
1 |
1.333333333 |
2. |
|
10 |
1.533851903 |
1.610544498 |
|
100 |
1.566893745 |
1.574728214 |
|
1000 |
1.570403873 |
1.571189075 |
|
10000 |
1.570757059 |
1.570835597 |
|
100000 |
1.570792400 |
1.570800254 |
Tab. 3: Numerische Werte
Mit CAS kann gezeigt werden:
![]() (10)
(10)
Die Konvergenz ist recht langsam.
Die Abbildung 6 illustriert den Grenzwert.
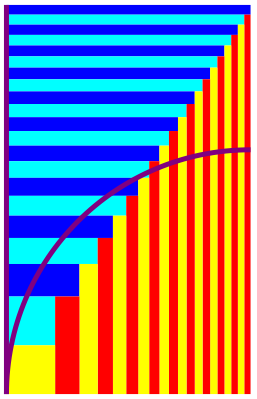
Abb. 6: Approximation des Viertelkreises
6 Die Gamma-Funktion
Die Folge xn kann auch mit der Gamma-Funktion beschrieben werden.
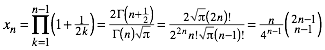 (11)
(11)
Wir kommen auf die Formel (7).