Hans Walser, [20090101a]
Wurzelberechnung nach einer Methode von Euler
1 Worum es geht
In [Euler 1802, Erster
Theil, Zweiter Abschnitt, Kapitel 12] beschreibt Euler einen Approximations-Algorithmus
zur Berechnung von Wurzeln. Das Verfahren ist im Wesentlichen die Methode von
Newton-Raphson, hat aber einen eleganten Bezug zur Taylor-Entwicklung und der binomischen
Formel.
2
Taylor
Fźr die Funktion 
erhalten wir die
k-te Ableitung:
Daraus ergibt sich die
Taylor-Entwicklung:
2.1
Sonderfall
Fźr 
bricht die Reihe
ab, da 
fźr 
. Somit ist:
Das ist die binomische
Formel.
3
Die Idee von Euler
3.1
Beispiel: Quadratwurzel
Wir wollen 
berechnen. Fźr 
erhalten wir:
Wir wŠhlen nun einen
Startwert 
und setzen 
. Dabei soll 
die Rolle von
obigem x und 
die Rolle von 
spielen. Bei Abbruch nach dem ersten Glied (dem
linearen Glied in 
) erhalten wir:
Wir nennen diesen
NŠhrungswert 
und iterieren.
Damit ergibt sich die Rekursion:
3.1.1
Vergleich mit Newton-Raphson
Wir bestimmen die
positive Nullstelle von 
. Wegen 
ergibt sich die
Rekursion:
Das ist dieselbe Formel
wie bei Euler.
3.1.2
Arithmetisches und geometrisches Mittel
In der Rekursion
ist 
das arithmetische
Mittel von 
und 
. Fźr das geometrische Mittel dieser beiden Zahlen erhalten
wir 
, also exakt die gesuchte Quadratwurzel. Das Verfahren von
Euler oder Newton-Raphson besteht also darin, dass das geometrische Mittel
durch das arithmetische Mittel approximiert wird.
3.2
Allgemein
Wir berechnen 
. Die Taylor-Entwicklung liefert:
Wir setzen 
und erhalten:
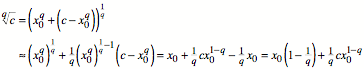
Durch Iteration ergibt
sich:
3.2.1
Beispiel kubische Wurzel
Fźr 
und 
erhalten wir:
Mit dem Startwert 
liefert Excel:
|
n |
xn |
|
0 |
7.000000000000 |
|
1 |
5.517006802721 |
|
2 |
5.046936042580 |
|
3 |
5.000435147754 |
|
4 |
5.000000037866 |
|
5 |
5.000000000000 |
|
6 |
5.000000000000 |
3.2.2
Vergleich mit Newton-Raphson
Wir bestimmen die
positive Nullstelle von 
. Wegen 
ergibt sich die
Rekursion:
Das ist dieselbe Formel
wie bei Euler.
3.2.3
Arithmetisches und geometrisches Mittel
Die Rekursion
kšnnen wir wie folgt
umformen:
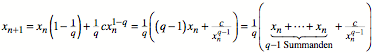
Somit ist 
das
arithmetische Mittel von 
Mal dem
Summanden 
sowie dem
Summanden 
. Fźr das geometrische Mittel dieser Glieder erhalten wir:
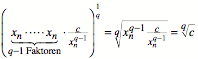
Dies ist der exakte
Wert der gesuchten Wurzel. Wir haben also auch hier eine Approximation des
geometrischen Mittels durch ein arithmetisches Mittel.
3.2.4
Andere Verteilung der Gewichte
Fźr die kubische Wurzel
hatten wir:
Die Zahlen 
und 
werden im
VerhŠltnis 2:1 gewichtet. Wir vertauschen nun die Gewichte und verŠndern ein
bisschen (damit der Vergleich mit dem geometrischen Mittel funktioniert):
Wenn wir hier zum
geometrischen Mittel źbergehen, ergibt sich:
Das sollte also
funktionieren. Fźr 
und 
liefert Excel:
|
n |
xn |
|
0 |
7.000000000000 |
|
1 |
5.150514182428 |
|
2 |
5.001105039459 |
|
3 |
5.000000061044 |
|
4 |
5.000000000000 |
|
5 |
5.000000000000 |
Das Verfahren ist also
noch ein bisschen schneller, hat aber den gro§en Nachteil, dass wir in der
Rekursion die Quadratwurzel benštigen.
Literatur
[Euler 1802] Euler, Leonhard: VollstŠndige
Anleitung zur Algebra. Leipzig, 1802