Hans Walser, [20190130]
Wurzel-2-Dreieck
Anregung: Horst Steibl, Braunschweig
1 Worum geht es?
Das
rechtwinklig gleichschenklige Dreieck (Abb. 1a) hat das SeitenverhŠltnis ![]() .
.
Wir
vertauschen nun die beiden LŠngen und arbeiten mit dem gleichschenkligen Dreieck
mit dem SeitenverhŠltnis ![]() (Abb. 1b). Dieses Dreieck nennen wir das Wurzel-2-Dreieck.
(Abb. 1b). Dieses Dreieck nennen wir das Wurzel-2-Dreieck.

Abb. 1: Rechtwinklig gleichschenkliges Dreieck und Wurzel-2-Dreieck
Beide Dreiecke kšnnen mit je drei Rechtecken im DIN-Format (Walser 2013) ausgelegt werden (Abb. 2).
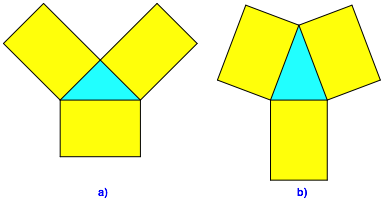
Abb. 2: DIN-Rechtecke
2 LŠngen und Winkel
Fźr das Wurzel-2-Dreieck mit der BasislŠnge 1 gelten folgende Ma§e (Bezeichnungen nach Abb. 3).
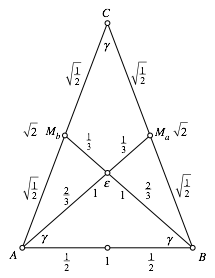
Abb. 3: Ma§e und Bezeichnungen
Es ist:
![]() (1)
(1)
Dieser
Winkel ![]() ist der Spitzenwinkel des Dreiecks, kommt
aber auch an anderen Orten vor.
ist der Spitzenwinkel des Dreiecks, kommt
aber auch an anderen Orten vor.
Weiter ist:
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
Weiter
gilt fźr die Schwerlinien ![]() und
und ![]() :
:
![]() (5)
(5)
Die
Dreiecke ![]() und
und ![]() sind daher ebenfalls Wurzel-2-Dreiecke.
sind daher ebenfalls Wurzel-2-Dreiecke.
3 Zerlegungen
Die Abbildung 4 zeigt eine Zerlegung des Wurzel-2-Dreieckes durch eine von einer Basisecke ausgehende Schwerlinie in zwei flŠchengleiche Dreiecke.

Abb. 4: Zerlegung
Das eine
der beiden Dreiecke (himmelblau) ist ebenfalls ein Wurzel-2-Dreieck. Das andere
(orange) Dreieck hat das SeitenverhŠltnis ![]() . Der Lehrer LŠmpel bringt hier die Bemerkung an, das
sei eine geometrische Folge. Wir bezeichnen dieses Dreieck mit dem sperrigen
Namen Wurzel-2-Nebendreieck.
. Der Lehrer LŠmpel bringt hier die Bemerkung an, das
sei eine geometrische Folge. Wir bezeichnen dieses Dreieck mit dem sperrigen
Namen Wurzel-2-Nebendreieck.
3.1 Zerlegung des Wurzel-2-Nebendreieckes
Das Wurzel-2-Nebendreieck kann in eine Folge von Wurzel-2-Dreiecken zerlegt werden (Abb. 5a). Dabei wird der FlŠcheninhalt der Dreiecke schrittweise halbiert. Die SchenkellŠnge des folgenden Dreieckes ist die BasislŠnge des vorhergehenden Dreieckes. Zusammen mit dem Wurzel-2-Dreieck unten rechts haben wir nun eine Zerlegung des ursprźnglichen Wurzel-2-Dreiecks in eine Folge von Wurzel-2-Dreiecken.
Diese Zerlegung erinnert an die Zerlegung des DIN A0-Rechteckes in Rechtecke DIN A1, A2, A3, ... (Walser 2013, S. 11, Abb. 1.4).
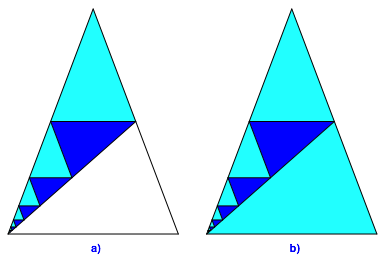
Abb. 5: Zerlegung
3.2 Zerlegung des Wurzel-2-Dreieckes
Wir kšnnen umgekehrt das Wurzel-2-Dreieck in eine Folge von Wurzel-2-Nebendreiecken zerlegen. Die Abbildung 6a zeigt eine einfache Lšsung mit dem Grenzpunkt rechts unten, die Abbildung 6b eine spiralfšrmige Lšsung mit einem Grenzpunkt im Innern. In der Abbildung 6a sind die orangen und die grźnen Dreiecke ungleichsinnig Šhnlich. In der Abbildung 6b sind alle Teildreiecke gleichsinnig Šhnlich.
Es gibt unendlich viele weitere Lšsungen.
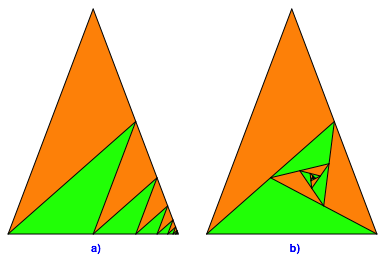
Abb. 6: Zerlegungen in Wurzel-2-Nebendreiecke
Frage: Gibt es analoge Zerlegungen fźr andere Dreiecke?
4 Falten
Das Wurzel-2-Dreieck kann durch Falten konstruiert werden. Dies geht sowohl mit einem Papier im DIN-Format wie auch mit einem quadratischen Origami-Papier. Beide Faltkonstruktionen sind exakt.
4.1 Papier im DIN-Format
Die Abbildung 7 zeigt den Faltvorgang. Zu Orientierungszwecken wird angenommen, das Papier sei vorne gelb und hinten magenta.
Die beiden schrŠgen Faltlinien definieren das Wurzel-2-Dreieck.
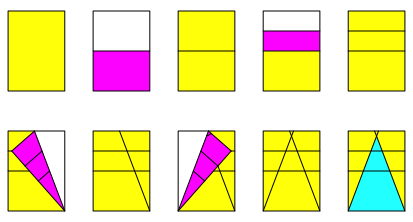
Abb. 7: Falten bei DIN-Papier
4.2 Quadratisches Origami Papier
Die Abbildung 8 zeigt den Faltvorgang.
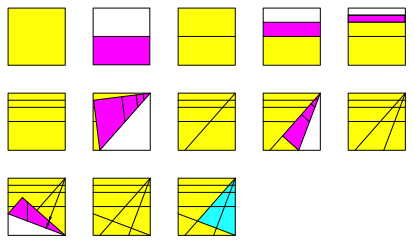
Abb. 8: Falten bei Origami-Papier
Wer clever ist, holt noch ein zweites Wurzel-2-Dreieck heraus.
5 Das Wurzel-2-Trapez
Wir
schneiden auf halber Hšhe die Spitze des Wurzel-2-Dreieckes ab (Abb. 9a). Es
bleibt ein gleichschenkliges Trapez źbrig. Durch Strecken mit dem Faktor ![]() erhŠlt die
Grundparallele die LŠnge
erhŠlt die
Grundparallele die LŠnge ![]() , die Schenkel erhalten die LŠnge 1 und die Deckparallele
die LŠnge
, die Schenkel erhalten die LŠnge 1 und die Deckparallele
die LŠnge ![]() , also den Kehrwert der Grundparallele (Abb. 9b). Die
Diagonalen erhalten ebenfalls die LŠnge
, also den Kehrwert der Grundparallele (Abb. 9b). Die
Diagonalen erhalten ebenfalls die LŠnge ![]() .
.
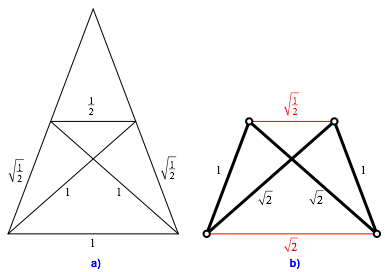
Abb. 9: Abschneiden zum Trapez
Dieses
Trapez kann als spezielle Position eines Gelenkmodells gesehen werden, das aus
den vier in der Abbildung 9b fett eingezeichneten StŠben der LŠngen ![]() und 1
besteht (Walser 2013, S. 37, 38, 44). Die beiden Parallelseiten haben dann
inverse LŠngen. Die Abbildung 10 zeigt zwei andere Positionen dieses
Gelenkmodells.
und 1
besteht (Walser 2013, S. 37, 38, 44). Die beiden Parallelseiten haben dann
inverse LŠngen. Die Abbildung 10 zeigt zwei andere Positionen dieses
Gelenkmodells.
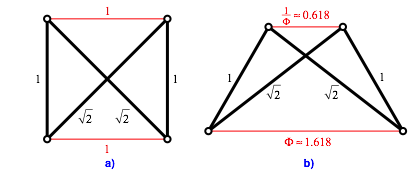
Abb. 10: Andere Positionen
6 Dimetrische Axonometrie
Den
Spitzenwinkel ![]() des Wurzel-2-Dreieckes treffen wir auch
bei der dimetrischen Axonometrie an (Abb. 11a mit den Einheitsvektoren auf den
Achsen). Ebenfalls treffen wir dort den Schnittwinkel
des Wurzel-2-Dreieckes treffen wir auch
bei der dimetrischen Axonometrie an (Abb. 11a mit den Einheitsvektoren auf den
Achsen). Ebenfalls treffen wir dort den Schnittwinkel ![]() der beiden Schwerlinien
der beiden Schwerlinien ![]() und
und ![]() an. Die
Winkel in der Abbildung 11 sind rein planimetrisch zu verstehen, nicht etwa
rŠumlich. Im Raum misst ja der Winkel zwischen der y-Achse und der z-Achse
90ˇ.
an. Die
Winkel in der Abbildung 11 sind rein planimetrisch zu verstehen, nicht etwa
rŠumlich. Im Raum misst ja der Winkel zwischen der y-Achse und der z-Achse
90ˇ.
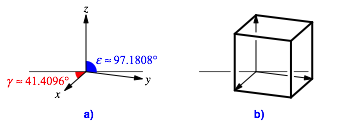
Abb. 11: Dimetrische Axonometrie
In der Abbildung 11b ist das dimetrische Bild des Einheitswźrfels eingetragen.
7 Rationale SeitenverhŠltnisse
Das
SeitenverhŠltnis im Wurzel-2-Dreieck ist irrational. Es gibt aber auch Dreiecke
mit rationalen SeitenverhŠltnissen, bei denen Vielfache (modulo 180ˇ) der
Winkel ![]() und
und ![]() erscheinen.
erscheinen.
7.1 SeitenverhŠltnis 3:2:2
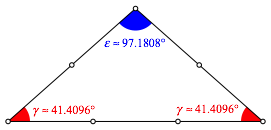
Abb. 12: SeitenverhŠltnis 3:2:2
Dieses Dreieck erscheint auch als Teildreieck in der Abbildung 3.
7.2 SeitenverhŠltnis 1:4:4
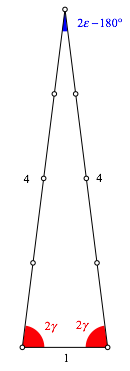
Abb. 13: SeitenverhŠltnis 1:4:4
Die Winkel sind modulo 180ˇ verdoppelt.
7.3 SeitenverhŠltnis 9:8:8
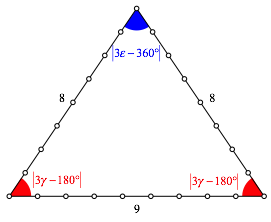
Abb. 14: SeitenverhŠltnis 9:8:8
Die Winkel sind modulo 180ˇ verdreifacht.
7.4 SeitenverhŠltnis 31:16:16

Abb. 15: SeitenverhŠltnis 31:16:16
Die Winkel sind modulo 180ˇ vervierfacht.
7.5 SeitenverhŠltnis 57:32:32

Abb.16: SeitenverhŠltnis 57:32:32
Die Winkel sind modulo 180ˇ verfźnffacht.
Frage: Gibt es ein analoges Vorgehen fźr andere Winkel?
7.6 †bersicht
7.6.1 Positive Zahlen
Die Tabelle 1 gibt eine †bersicht.
|
Faktor |
Basis |
Schenkel |
Schenkel |
|
1 |
3 |
2 |
2 |
|
2 |
1 |
4 |
4 |
|
3 |
9 |
8 |
8 |
|
4 |
31 |
16 |
16 |
|
5 |
57 |
32 |
32 |
|
6 |
47 |
64 |
64 |
|
7 |
87 |
128 |
128 |
|
8 |
449 |
256 |
256 |
|
9 |
999 |
512 |
512 |
|
10 |
1201 |
1024 |
1024 |
Tab. 1: †bersicht
Fźr den Vervielfachungsfaktor n ist die SchenkellŠnge:
![]() (6)
(6)
Fźr die BasislŠnge gilt:
![]() (7)
(7)
7.6.2 Weglassen der Betragsstriche
Mit
![]() (8)
(8)
erhalten wir die Werte der Tabelle 2.
|
n |
|
|
|
1 |
3 |
2 |
|
2 |
1 |
4 |
|
3 |
–9 |
8 |
|
4 |
–31 |
16 |
|
5 |
–57 |
32 |
|
6 |
–47 |
64 |
|
7 |
87 |
128 |
|
8 |
449 |
256 |
|
9 |
999 |
512 |
|
10 |
1201 |
1024 |
Tab. 2: Mit Minuszeichen
Bei der
Folge ![]() handelt es
sich um die Folge A247563 der oeis. Sie hat die
Rekursion:
handelt es
sich um die Folge A247563 der oeis. Sie hat die
Rekursion:
![]() (9)
(9)
Weblinks
Oeis, The On-Line Encyclopedia for Integer
Sequences:
Horst Steibl, Braunschweig:
Hans Walser: Miniaturen: DIN-Format:
http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/DIN_Format/index.html
Literatur
Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.