1 Worum geht es?

Wir teilen Dreieckswinkel (Innenwinkel) zu gleichen Anteilen. Dies führt zu drei Schnittpunkten von jeweils drei Geraden.

2 Ausgangsfigur

Wir reduzieren einen Dreieckswinkel symmetrisch von den Schenkeln her um denselben Anteil. In der Abbildung 1 ist der Anteil ein Fünftel. Der Anteil braucht aber nicht rational zu sein.

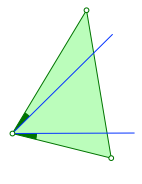
Abb. 1: Von beiden Schenkeln um den gleichen Anteil zurück.

Wir wiederholen das Spielchen mit demselben Anteil bei den beiden anderen Dreieckswinkeln (Abb. 2).

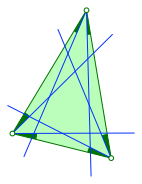
Abb. 2: Alle drei Winkel in gleichen Anteilen reduziert

Es geht auch nach außen (Abb. 3). Die Anteile des jeweiligen Innenwinkels werden nach außen abgetragen.

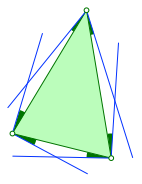
Abb. 3: Nach außen

3 Erster Schnittpunkt

Die Abbildung 4 zeigt einen Schnittpunkt von drei Geraden (Strecken) in der Figur der Abbildung 2. Verifikation mit DGS.

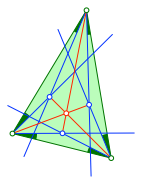
Abb. 4: Ein Schnittpunkt

In der Abbildung 5 wird der Winkelanteil variiert. Ist der Winkelanteil genau die Hälfe, ergibt sich der Winkelhalbierenden-Schnittpunkt.

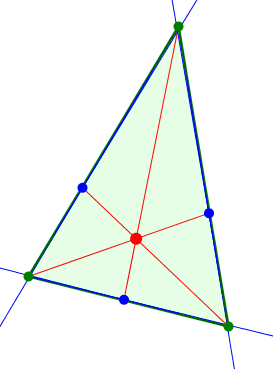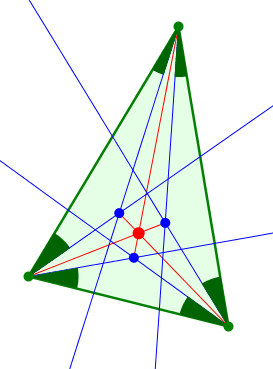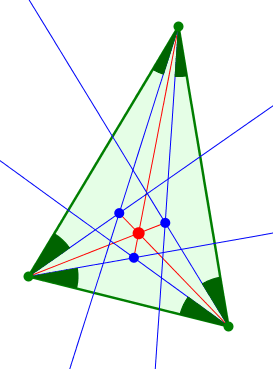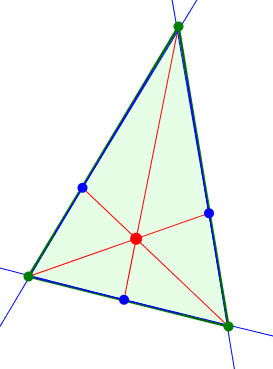
Abb. 5: Variation des Winkelanteils

Werden die Innenwinkelanteile nach außen abgetragen, ergeben sie die Figuren der Abbildungen 6 und 7.

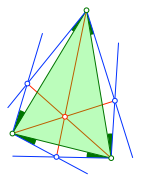
Abb. 6: Innenwinkelanteile nach außen abgetragen

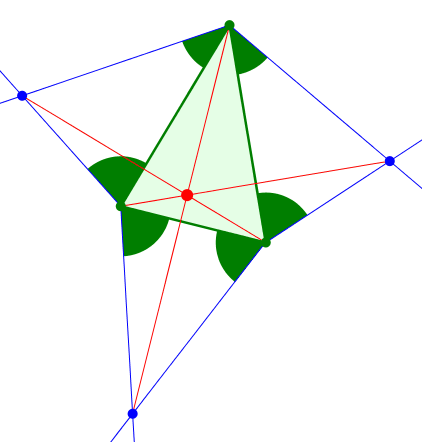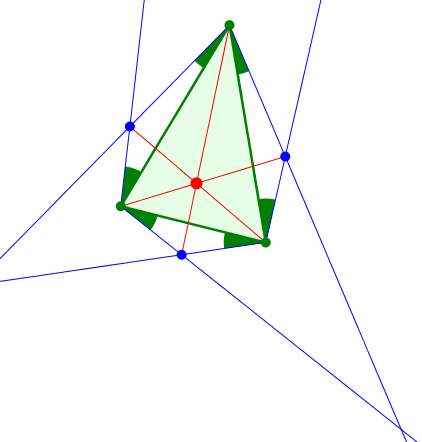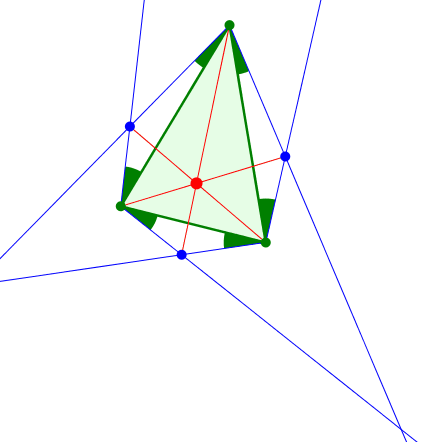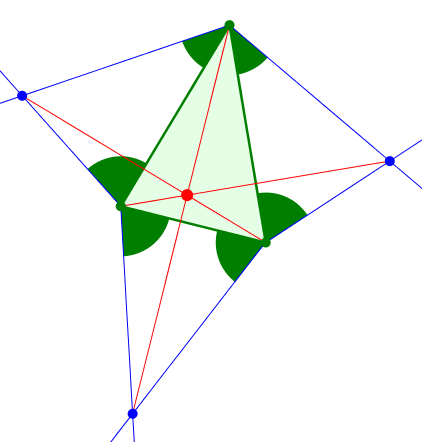
Abb. 7: Außen

4 Grenzfall

Interessant ist natürlich der Durchgang der blauen Punkte durch die Dreiecksseiten (Abb. 8). In diesem Fall sind die blauen Punkte Schnittpunkte von zwei aufeinanderfallenden Geraden. Das geht natürlich nicht. Wenn man genau aufpasst, merkt man, dass der Computer das Problem überhupft.

Abb. 8: Durchgang durch die Dreiecksseiten

Wir können die Sache retten, indem wir in diesem Grenzfall die blauen Punkte als Teilpunkte der Dreiecksseiten im Verhältnis der anliegenden Innenwinkel des Dreiecks sehen (Abb. 9).

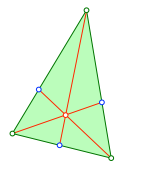
Abb. 9: Teilung im Verhältnis der Innenwinkel. Innenwinkelschwerpunkt

Nach dem Satz von Ceva schneiden sich die drei Ecktransversalen durch die blauen Punkte in einem Punkt. Dieser Punkt ist der Innenwinkelschwerpunkt.

5 Ein weiterer Schnittpunkt

Die Abbildungen 10 und 11 zeigen einen weiteren Schnittpunkt. Allerdings ist dieser Schnittpunkt gar nicht so sehr verschieden vom Schnittpunkt der Abbildung 4. Es wird einfach mit den Ergänzungsanteilen der Winkelanteile gearbeitet.

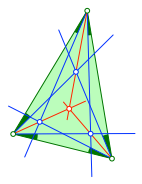
Abb. 10: Ein weiterer Schnittpunkt

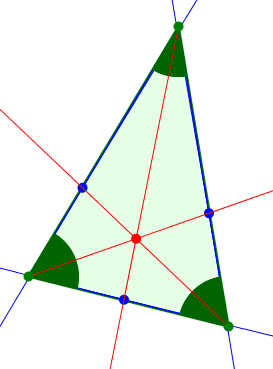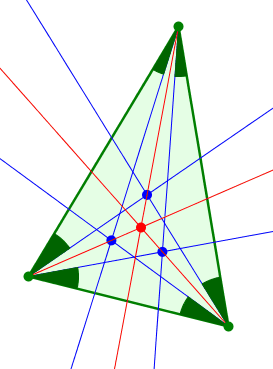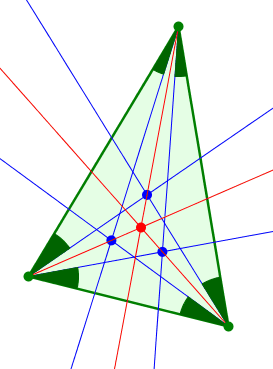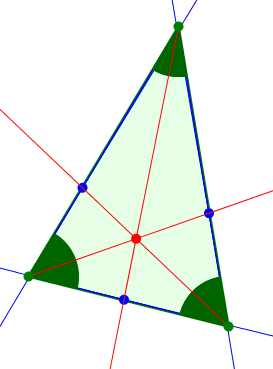
Abb. 11: Ein weiterer Schnittpunkt

6 Und noch ein Schnittpunkt

Die Abbildungen 12 und 13 zeigen noch einen Schnittpunkt. Er basiert auf einem Sechseck.

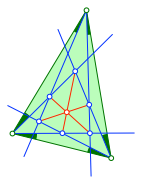
Abb. 12: Noch ein Schnittpunkt

Abb. 13: Noch ein Schnittpunkt

Weblink

Hans Walser: Winkelschwerpunkte

http://www.walser-h-m.ch/hans/Miniaturen/W/Winkelschwerpunkte/Winkelschwerpunkte.html

Hans Walser: Winkelteilung

http://www.walser-h-m.ch/hans/Miniaturen/W/Winkelteilung2/Winkelteilung2.html