Hans Walser, [20160324]

Der Satz von Viviani im Raum

1 Ausgangslage

Der Satz von Viviani besagt, dass in einem gleichseitigen Dreieck die Summe der drei von einem beliebigen Punkt ausgehenden Abstände zu den Dreieckseiten eine Konstante ist, nämlich die Dreieckshöhe (Vargyas und Walser, 2015).

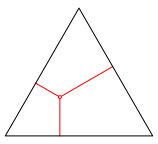
Abb. 1: Der Satz von Viviani in der Ebene

Ein einfacher Beweis geht so: Wir zerlegen das Dreieck in drei Teildreiecke. In der Abbildung 2 ist eines dieser Teildreiecke hervorgehoben.

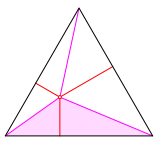
Abb. 2: Teildreiecke

Die Teildreiecke haben eine Seite des Ausgangsdreiecks als Grundlinie und eine rote Abstandsstrecke als Höhe. Der Flächeninhalt eines Teildreiecks ist also die Hälfte des Produktes der Dreiecksseite mit der Abstandsstrecke. Die Summe der drei Flächeninhalte ist somit die Hälfte des Produkts der Dreiecksseite mit der Summe der drei roten Abstandsstrecken. Andererseits ist das die Gesamtfläche des Dreiecks, also die Hälfte des Produkts der Dreiecksseite mit der Dreieckshöhe. Somit ist die Summe der drei roten Abstandsstrecken gleich der Dreieckshöhe. Dies war zu zeigen.

2 Im Raum

Der Satz gilt entsprechend im Raum: In einem regulären Tetraeder ist die Summe der vier von einem beliebigen Punkt ausgehenden Abstände zu den Tetraederseitenflächen eine Konstante, nämlich die Tetraederhöhe. Nachfolgend zunächst ein rechnerischer Beweis.

3 Disposition im Koordinatensystem

Die Punkte seien die vier Eckpunkte des Tetraeders. Das Tetraeder kann in den Einheitswürfel eingebettet werden (Abb. 3).

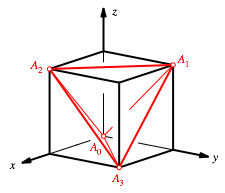
Abb. 3: Tetraeder im Einheitswürfel

Damit sind

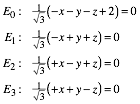(1)

die Normalformen der Ebenengleichungen der Seitenflächen des Tetraeders.

4 Abstandssumme

Wir bezeichnen mit die Summe der Abstände eines Punktes von den vier Tetraederseitenflächen. Es ist:

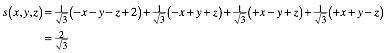(2)

Die Summe ist also unabhängig vom Punkt und konstant.

Wenn wir den Punkt P gegen eine Tetraederecke bewegen, wird einer der vier Abstände gleich groß wie die Tetraederhöhe und die drei anderen Abstände werden null.

Dies war zu beweisen.

Der Beweis ist formal recht einfach, aber geometrisch nicht elegant.

Die Abbildung 4 illustriert die Situation. Die Längensumme der vier blauen Strecken ist konstant und gleich groß wie die Tetraederhöhe.

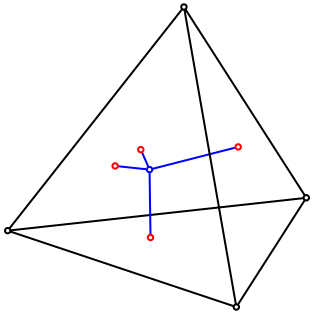
Abb. 4: Summe der Abstände

5 Geometrischer Beweis

Wir zerlegen das Tetraeder, vom blauen Punkt ausgehend, in vier Dreikant-Pyramiden mit je einer Seitenfläche des Tetraeders als Grundfläche. Die Abbildung 5 zeigt eine der vier Pyramiden.

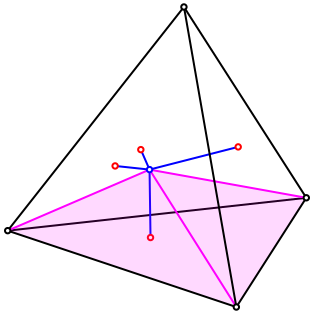
Abb. 5: Pyramide

Die Pyramide hat eine der blauen Strecken als Höhe. Das Volumen ist also ein Drittel des Produktes der blauen Streckenlänge mit der Seitenfläche des Tetraeders. Die Volumensumme der vier Pyramiden ist somit einerseits die ein Drittel des Produktes der Summe der blauen Streckenlängen mit der Seitenfläche des Tetraeders. Andererseits ist das aber das gesamte Tetraedervolumen, also ein Drittel des Produktes der Tetraederhöhe mit der Seitenfläche des Tetraeders.

Daher ist die Tetraederhöhe gleich der Summe der vier blauen Streckenlängen. Dies war zu zeigen.

6 Eine Flächensumme

Die roten Fußpunkte der vier blauen Strecken in den Abbildungen 4 und 5 liegen je in einer der vier Seitenflächen des Tetraeders. Wir zeichnen nun ausgehend von jedem roten Punkt die ebene Viviani-Figur im betreffenden gleichseitigen Dreieck (rot in Abb. 6).

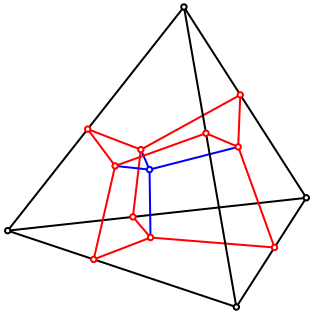
Abb. 6: Viviani-Figuren in den Seitendreiecken

Die Abstandsfußpunkte der Viviani-Figuren auf benachbarten Seitendreiecken liegen im selben Punkt auf der gemeinsamen Tetraederkante. Dies muss so sein, da die beiden Abstandsstrecken in der Normalebene zur Tetraederkante durch den ursprünglichen blauen Startpunkt im Innern des Tetraeders liegen.

Wir können also orthogonal zu jeder Tetraederkante ein ebenes Viereck einzeichnen. Die Abbildung 7 zeigt ein solches Viereck.

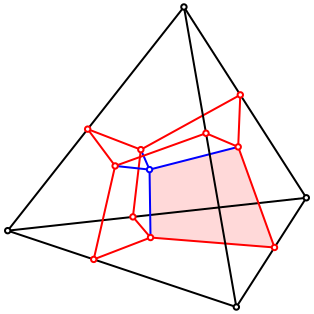
Abb. 7: Viereck

Das Viereck ist von zwei blauen und zwei roten Kanten begrenzt. Eine blaue und die anschließende rote Kante sind orthogonal zueinander. Das Viereck kann also in zwei rechtwinklige Dreiecke zerlegt werden, was die Flächenberechnung sehr einfach macht.

Die Abbildung 8 zeigt alle sechs Vierecke.

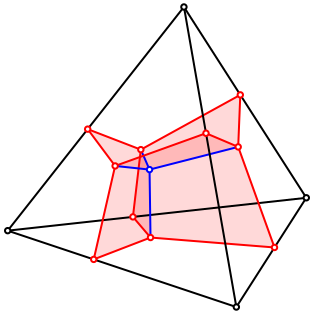
Abb. 8: Die sechs Vierecke

Der Flächensatz von Viviani besagt nun, dass die Summe der sechs Viereckflächen unabhängig vom blauen Startpunkt im Tetraeder ist und daher konstant.

Für den Beweis zerlegen wir die Vierecke in rechtwinklige Dreiecke. Die Abbildung 9 zeigt exemplarisch drei solcher Dreiecke, welche eine blaue Strecke als gemeinsame Kathete haben.

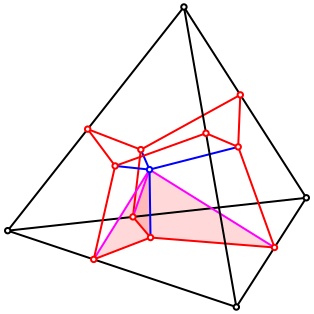
Abb. 9: Drei rechtwinklige Dreiecke

Die Flächensumme dieser drei rechtwinkligen Dreiecke ist die Hälfte des Produktes der gemeinsamen blauen Kathetenlänge mit der Summe der drei roten Kathetenlängen. Die Summe der drei roten Kathetenlängen ist aber nach dem Satz von Viviani in der Ebene gleich der Höhe eines Seitendreieckes.

Für die Summe aller Viereckflächen erhalten wir somit die Hälfte des Produktes der Höhe eines Seitendreieckes mit der Summe der vier blauen Strecken. Die Summe der vier blauen Strecken ist aber nach dem Satz von Viviani im Raum die Tetraederhöhe.

Die Summe aller Viereckflächen ist also die Hälfte des Produktes der Seitendreieckhöhe mit der Tetraederhöhe. Damit ist der Flächensatz bewiesen.

Literatur

Vargyas, Emese und Walser, Hans (2015): Verallgemeinerung des Satzes von Viviani. MI, Mathematikinformation Nr. 63, 15. September 2015. ISSN 1612-9156. S. 3-10.