Hans Walser, [20210721]
Vielecke abdichten
0 Worum geht es?
Die Abbildung 1 zeigt ein regelmäßiges Zehneck, das von außen mit zehn regelmäßigen Fünfecken eingemauert ist.
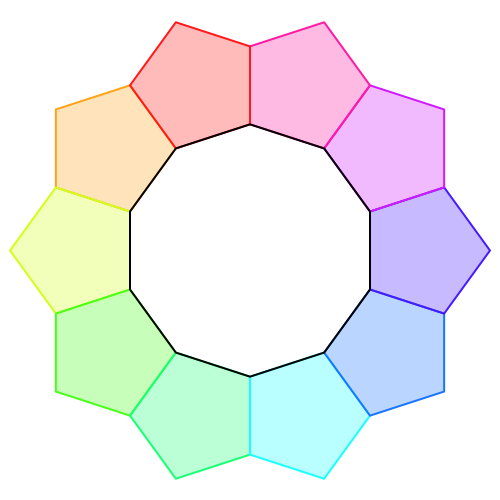
Abb. 1: Eingemauertes Zehneck
Kann ein regelmäßiges Vieleck von innen her mit regelmäßigen Vielecken abgedichtet werden?
1 Die triviale Lösung
Jedes regelmäßige Vieleck kann mit sich selber von innen her abgedichtet werden.
2 Nichttriviale Lösung
An jeder Ecke des Vieleckes kommen zwei Dichtungsvielecke zusammen. Deren Innenwinkel ist halb so groß wie der Innenwinkel des gegebenen Vieleckes und damit kleiner als 90°. Als Dichtungsvielecke kommen daher nur gleichseitige Dreiecke in Frage. Dann hat das gegebene Vieleck Innenwinkel 120°. Es muss ein regelmäßiges Sechseck sein (Abb. 2).
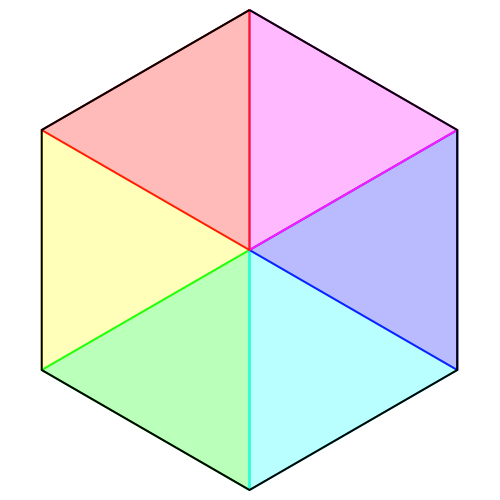
Abb. 2: Die einzige nichttriviale Lösung
3 Etwas Rechnung
Wir wollen auch rechnerisch zeigen, dass das Sechseck die einzige Lösung ist.
Dazu
wollen wir ein regelmäßiges n-Eck abdichten. Es hat den Innenwinkel a :
![]() (1)
(1)
Somit hat das Dichtungsvieleck
den Innenwinkel b :
![]() (2)
(2)
Für den Außenwinkel g und damit den Zentriwinkel des
Dichtungsvielecks ergibt sich:
![]() (3)
(3)
Daraus ergibt sich für die
Eckenzahl en des Dichtungsvieleckes:
![]() (4)
(4)
Die Tabelle 1 gibt die ersten
Werte für en.
|
n |
e |
e |
|
n |
e |
e |
|
3 |
12/5 |
2.4 |
|
22 |
11/3 |
3.666666667 |
|
4 |
8/3 |
2.666666667 |
|
23 |
92/25 |
3.68 |
|
5 |
20/7 |
2.857142857 |
|
24 |
48/13 |
3.692307692 |
|
6 |
3 |
3 |
|
25 |
100/27 |
3.703703704 |
|
7 |
28/9 |
3.111111111 |
|
26 |
26/7 |
3.714285714 |
|
8 |
16/5 |
3.2 |
|
27 |
108/29 |
3.724137931 |
|
9 |
36/11 |
3.272727273 |
|
28 |
56/15 |
3.733333333 |
|
10 |
10/3 |
3.333333333 |
|
29 |
116/31 |
3.741935484 |
|
11 |
44/13 |
3.384615385 |
|
30 |
15/4 |
3.75 |
|
12 |
24/7 |
3.428571429 |
|
31 |
124/33 |
3.757575758 |
|
13 |
52/15 |
3.466666667 |
|
32 |
64/17 |
3.764705882 |
|
14 |
7/2 |
3.5 |
|
33 |
132/35 |
3.771428571 |
|
15 |
60/17 |
3.529411765 |
|
34 |
34/9 |
3.777777778 |
|
16 |
32/9 |
3.555555556 |
|
35 |
140/37 |
3.783783784 |
|
17 |
68/19 |
3.578947368 |
|
36 |
72/19 |
3.789473684 |
|
18 |
18/5 |
3.6 |
|
37 |
148/39 |
3.794871795 |
|
19 |
76/21 |
3.619047619 |
|
38 |
19/5 |
3.8 |
|
20 |
40/11 |
3.636363636 |
|
39 |
156/41 |
3.804878049 |
|
21 |
84/23 |
3.652173913 |
|
40 |
80/21 |
3.809523810 |
Tab. 1: Eckenzahlen der Abdichtungsvielecke
Für n = 6 ergibt sich der schon gefundene Wert e6
= 3
Die Folge en ist monoton wachsend mit dem Grenzwert 4.
Daher gibt es keine weiteren ganzzahligen Lösungen für das Verpackungsvieleck
mehr. Zwischen e6 = 3 und dem Grenzwert 4 gibt es keine weiteren ganzen Zahlen. Basta
4
Sterne
In der zweiten Spalte der Tabelle 1 ist en als
gekürzter Bruch angegeben. Zum Beispiel ist e3 = 12/5. Wir können diesen Bruch als Stern
interpretieren. Auf einem Kreis werden 12 Punkte regelmäßig verteilt. Wir
starten in einem Punkt und gehen weiter zum fünften Punkt. Und so weiter
jeweils zum fünftnächsten Punkt. So entsteht ein Stern (Abb. 3).
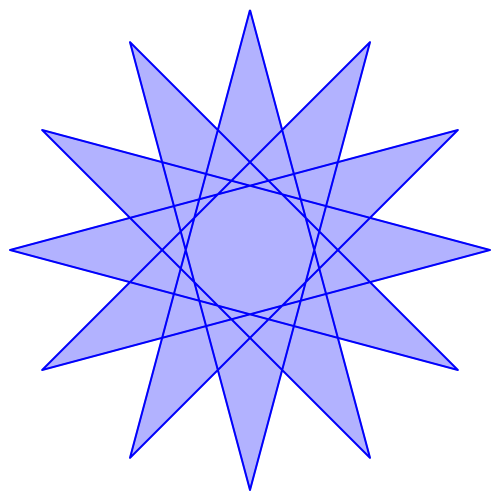
Abb. 3: Der 12/5-Stern
Wenn wir solche Sterne als Verpackungsvielecke zulassen, ergibt sich
auch für n = 3 eine Lösung (Abb. 4).
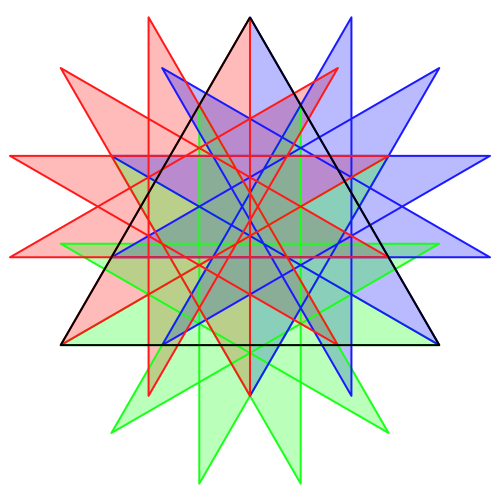
Abb. 4: Abgedichtetes Dreieck
5
Weitere
Beispiele
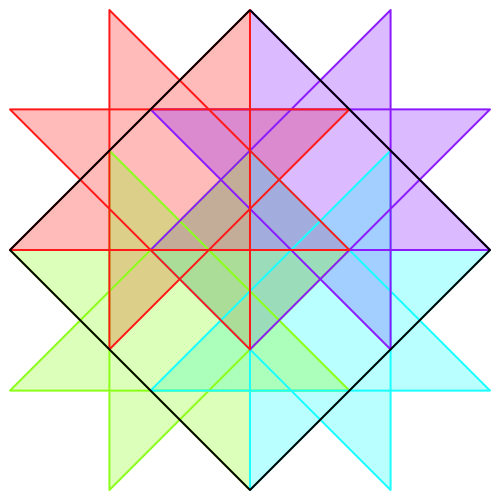
Abb. 5: n = 4, e = 8/3
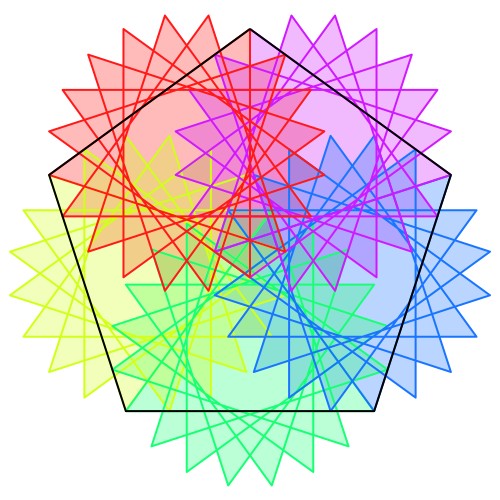
Abb. 6: n = 5, e = 20/7
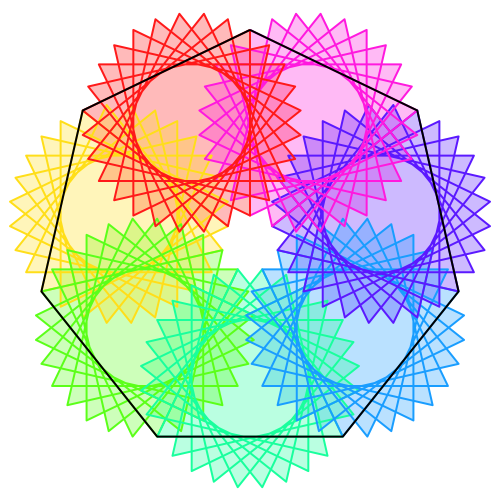
Abb. 7: n = 7, e = 28/9
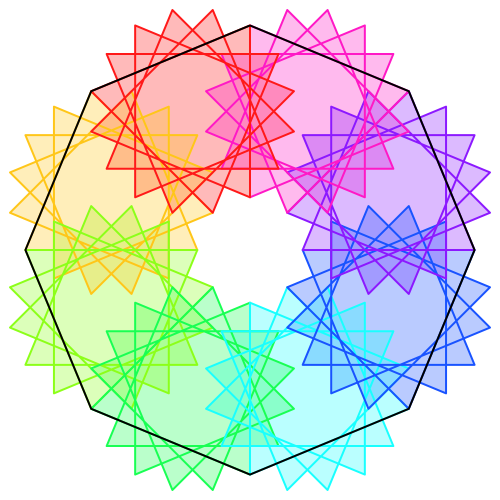
Abb. 8: n = 8, e = 16/5
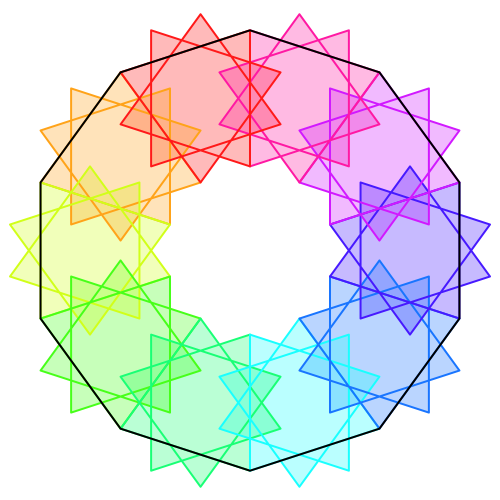
Abb. 9: n = 10, e = 10/3
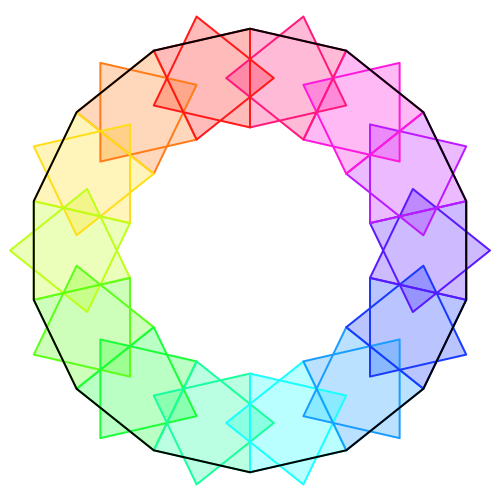
Abb. 10: n = 14, e = 7/2
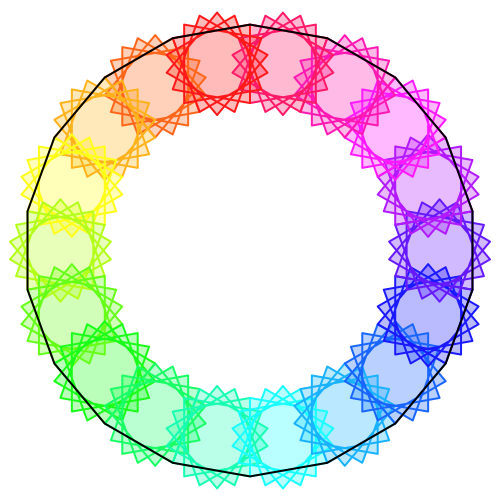
Abb. 11: n = 18, e = 18/5
Website
Hans Walser: Vielecke einpacken
http://www.walser-h-m.ch/hans/Miniaturen/V/Vielecke_einpacken/Vielecke_einpacken.html