1 Der Strahlensatz

In der Schule lernen wir den Strahlensatz.

Wir schneiden ein Geradenbüschel mit einer Schar paralleler Geraden (Abb. 1).

Dann sind die Teilverhältnisse auf den roten Büschelgeraden gleich.

Ebenso sind die Teilverhältnisse auf den blauen parallelen Geraden gleich.

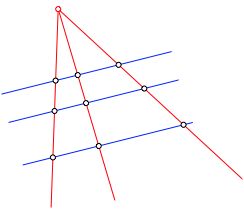
Abb. 1: Strahlensatz

Umkehrungen:

Wenn wir auf zwei Büschelgeraden gleiche Teilverhältnisse haben, sind die Verbindungsgeraden der Teilpunkte parallel.

Wenn wir auf zwei parallelen Geraden gleiche Teilverhältnisse haben, sind die Verbindungsgeraden der Teilpunkte kopunktal.

2 Tangenten an eine Parabel

Wir zeichnen drei rote und drei blaue Tangenten an eine Parabel (Abb. 2) und scheiden diese Tangenten wechselseitig.

Abb. 2: Tangenten an Parabel

Dann sind die Teilverhältnisse auf den roten Tangenten gleich. Ebenso sind die Teilverhältnisse auf den blauen Tangenten gleich.

3 Beweis

Für den Beweis arbeiten wir mit der Standardparabel y = x². Das ist keine Einschränkung der Allgemeinheit, da alle Parabeln ähnlich sind.

Die Parabeltangente im Punkt hat die Gleichung:

Wir arbeiten mit den vier Tangenten der Abbildung 3.

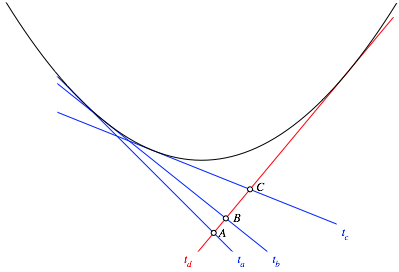
Abb. 3: Beweisfigur

Für diese vier Tangenten verwenden wir die Gleichungen:

Für die Schnittpunkte A, B und C ergeben sich daraus die Koordinaten:

Für die Abstände dieser Punkte erhalten wir:

Somit ist:

Dieses Verhältnis ist unabhängig vom Parameter d, es ist also für alle roten Tangenten gleich. Aus Symmetriegründen sind ebenso die Teilverhältnisse auf den blauen Tangenten gleich.

4 Link

Den Link zwischen dem schulmäßigen Strahlensatz und der Verhältnisgleichheit bei Parabeltangentenabschnitten finden wir wie folgt.

Wir denken uns die Parabel gegeben durch Brennpunkt F und Leitlinie l. Eine Parabeltangente finden wir nun, indem wir auf der Leitlinie l einen Punkt wählen. Die Mittelsenkrechte zwischen diesem Punkt und dem Brennpunkt F ist dann eine Tangente an die Parabel. Die Abbildung 4 illustriert das an zwei Beispielen.

Man beachte, dass der Mittelpunkt zwischen dem Punkt auf der Leitlinie l und dem Brennpunkt F auf der Scheiteltangente der Parabel liegt.

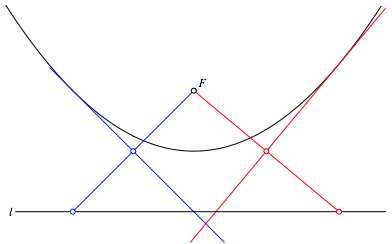
Abb. 4: Parabeltangenten

Und nun machen wir einen Grenzübergang, indem wir den Brennpunkt F an die Leitgerade l annähern. Dadurch wird die Parabel immer schmaler und steiler. Im Limes haben wir eine doppelt durchlaufene Halbgerade vom Lotfußpunkt von F auf l nach oben.

Die Tangenten behandeln wir unterschiedlich.

Bei den blauen Tangenten lassen wir den Punkt auf der Leitlinie l unverändert. Dadurch werden die blauen Tangenten aufgestellt und sind im Limes senkrecht zur Leitlinie l also untereinander parallel.

Bei den roten Tangenten lassen wir die Richtung unverändert. Im Limes verlaufen alle roten Tangenten durch den Lotfußpunkt von F auf l.

Die Abbildung 5 zeigt die ersten Schritte mit je einer blauen und einer roten Tangente.

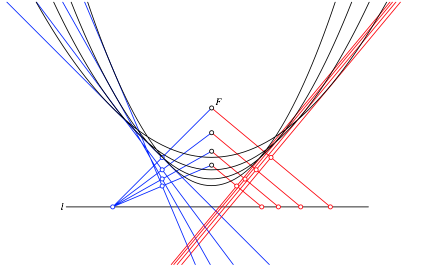
Abb. 5: Der Brennpunkt nähert sich der Leitlinie an

Die Abbildung 6 zeigt, was sich aus der Figur der Abbildung 2 nach diesem Grenzübergang ergibt. Das ist der klassische Strahlensatz.

Die Teilverhältnisse auf den roten beziehungsweise auf den blauen Tangenten sind in den Abbildung 2 und 6 die gleichen.

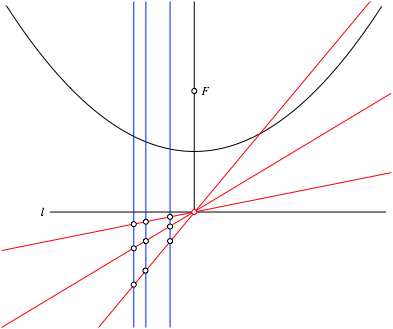
Abb. 6: Strahlensatz

5 Winkeleisensatz

Wir können uns eine Variante der Strahlensatz-Verallgemeinerung ausdenken, indem wir mit rechten Winkeln arbeiten (Abb. 7). Der Beweis sei der Leserin überlassen.

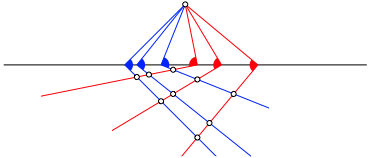
Abb. 7: Winkeleisensatz