Hans Walser, [20181217]
Trigonometrische Identitt
1 Die Identitt
Fr eine Ungerade Zahl m = 2n + 1 gilt:
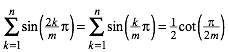 (1)
(1)
Detailliert:
 (1a)
(1a)
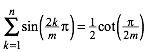 (1b)
(1b)
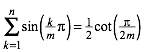 (1c)
(1c)
2 Die Rei§verschlusssymmetrie
Die Abbildungen 1 und 2 illustrieren die Beziehung (1a) exemplarisch fr m = 9, also fr n = 4, im Einheitskreis und an der Sinuskurve.
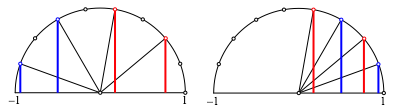
Abb. 1: Im Einheitskreis

Abb. 2: Sinuskurve
Wir haben eine Rei§verschlusssymmetrie (Abb. 3). Gegenberliegende Teile passen in die Lcken.

Abb. 3: Rei§verschluss
3 Geometrischer Zugang
Wir
beweisen die Beziehung (1b). In einem Winkelfeld mit dem Scheitelwinkel ![]() tragen wir die Einheitsstrecke vom
Scheitel ausgehend abwechslungsweise nach oben und nach unten ab. Die Abbildung
4 illustriert das Vorgehen fr n = 4,
also m = 9. Nach Walser (1988) kommen
wir nach m Schritten zum
Scheitelpunkt zurck.
tragen wir die Einheitsstrecke vom
Scheitel ausgehend abwechslungsweise nach oben und nach unten ab. Die Abbildung
4 illustriert das Vorgehen fr n = 4,
also m = 9. Nach Walser (1988) kommen
wir nach m Schritten zum
Scheitelpunkt zurck.
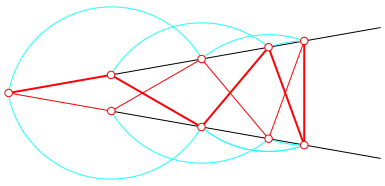
Abb. 4: Abtragen der Einheitsstrecke
Die dabei
auftretenden Winkel sind Vielfache von ![]() (Abb. 5). Aus Symmetriegrnden ist steht
die n + erste Strecke rechtwinklig
zur Winkelhalbierenden des Winkelfeldes.
(Abb. 5). Aus Symmetriegrnden ist steht
die n + erste Strecke rechtwinklig
zur Winkelhalbierenden des Winkelfeldes.
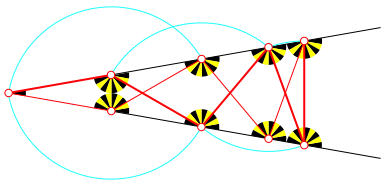
Abb. 5: Winkel
Wir knnen n gleichschenklige Dreiecke der Schenkellnge 1 einpassen (Abb. 6).
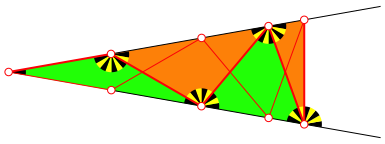
Abb. 6: Gleichschenklige Dreiecke
Diese gleichschenkligen Dreiecke haben vom Scheitelpunkt ausgehend der Reihe nach die Spitzenwinkel:
![]() (2)
(2)
Also:
![]() (3)
(3)
Fr die Flcheninhalte dieser Dreiecke erhalten wir:
![]() (4)
(4)
Die Summe der Flcheninhalte ist also:
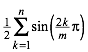 (5)
(5)
Diese
Dreiecke bilden zusammen ein gr§eres gleichschenkliges Dreieck mit dem Spitzenwinkel
![]() und der Basislnge 1. Es hat den
Flcheninhalt:
und der Basislnge 1. Es hat den
Flcheninhalt:
![]() (6)
(6)
Aus (5) und (6) folgt (1b).
4 Formaler Beweis
Wir zeigen (1c).
Zunchst eine Hilfsformel, eine Art Additionstheorem:
![]() (7)
(7)
Beweis der Hilfsformel mit dem Additionstheorem fr den Kosinus:
 (8)
(8)
Wir schreiben die Formel (1c) in der Form:
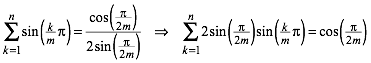 (9)
(9)
Wegen (8) kann das
in der Form geschrieben werden:
 (10)
(10)
Wegen m = 2n
+ 1 haben wir im letzten Summanden einen rechten Winkel. Dieser Summand
verschwindet also auch. Es bleibt nur der erste Summand brig. Damit sind (9)
und (1c) bewiesen.
Literatur
Walser, Hans (1988): Ein Schlie§ungssatz der Elementargeometrie. Elemente der Mathematik (43), 1988. S. 161-169.