1 Worum geht es?

Es wird ein Konstruktionsalgorithmus skizziert, um zu n beliebig vorgegebenen Punkten ein Steiner-Netz zu finden.

Der Konstruktionsalgorithmus wird für ein Beispiel mit n = 7 gezeigt.

Das Verfahren erinnert an die Organisation eines K.-o.-Turniers.

2 Der Algorithmus

Wir beginnen mit n vorgegebenen Punkten (Abb. 1).

Abb. 1: Sieben gegebene Punkte

Wir errichten auf je zweien der Punkte ein gleichseitiges Dreieck (rot in Abb. 2). Bei einer ungeraden Punktzahl n geht das nicht auf. Da lassen wir einfach einen Punkt außen vor und beziehen ihn erst in der nächsten Runde mit ein. Bei einem K.-o.-Turnier macht man das ja auch so.

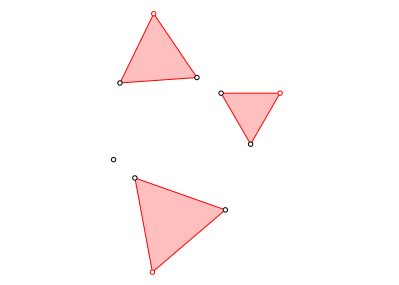
Abb. 2: Erste Runde: Drei rote Dreiecke

Nun verfahren wir mit den jeweils dritten Punkten der roten Dreiecke sowie allenfalls einem noch nicht verarbeiteten Startpunkt genau so. Auf je zweien wird ein gleichseitiges Dreieck errichtet (blau in Abb. 3).

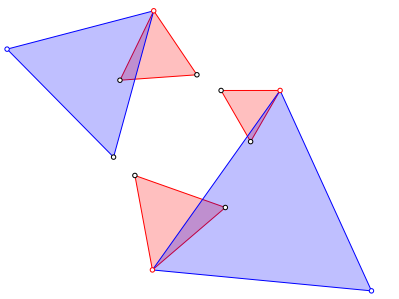
Abb. 3: Zweite Runde: Zwei blaue Dreiecke

Nun haben wir noch zwei dritte Punkte. Diese verbinden wir mit einer Strecke (magenta in Abb. 4). Wir werden sehen, dass diese Strecke so lang ist wie das gesamte zukünftige Steiner-Netz.

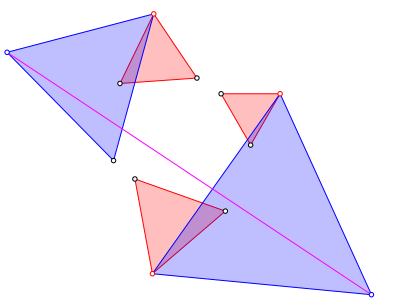
Abb. 4: Magenta Strecke.

Zu den zuletzt gezeichneten Dreiecken zeichnen wir die Umkreise und schneiden mit der magenta Strecke (Abb. 5). Dies sind die innersten Verzweigungspunkte. Wir verbinden sie mit den dritten Punkten der roten Dreiecke (orange in Abb. 5).

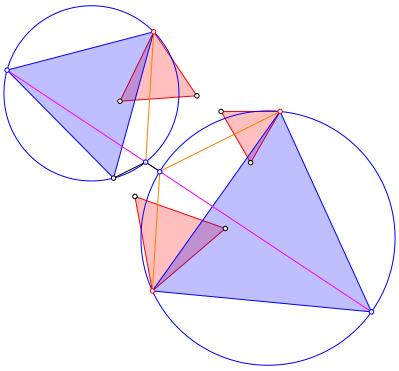
Abb. 5: Erste Verzweigungspunkte

Nun zeichnen wir die Umkreise der roten Dreiecke und schneiden mit den orangen Strecken (Abb. 6). Diese Punkte sind die Verzweigungspunkte zweiter Ordnung. Wir verbinden sie mit den schwarzen Basispunkten der roten Dreiecke.

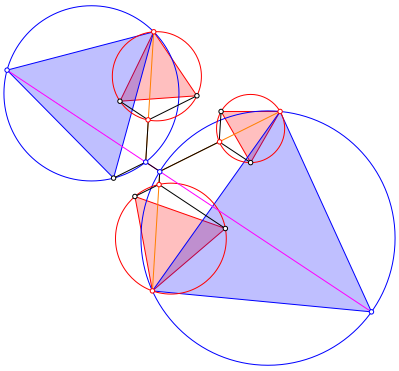
Abb. 6: Verzweigungspunkte zweiter Ordnung

In unserem Beispiel sind wir nun durch. Die Abbildung 7 zeigt das Steiner-Netz ohne die konstruktiven Hilfsfiguren.

Bei einer größeren Anzahl von gegebenen Punkten müssen entsprechend mehr Runden durchgespielt werden.

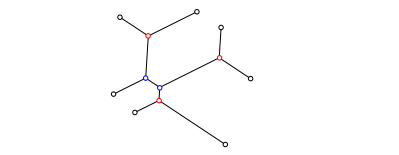
Abb. 7: Steiner-Netz

3 Kommentare und Ergänzungen

3.1 Fermat-Punkt

Falls am Schluss des Dreiecke-Zeichnens drei Punkte übrigbleiben (zum Beispiel bei 5 oder 9 Startpunkten), zeichnen wir zu diesen drei Punkten den Fermat-Punkt und fahren sinnvoll weiter.

3.2 Arbeisaufwand

Die Anzahl der benötigten Runden geht mit dem Zweierlogarithmus der Anzahl Startpunkte.

3.3 Van Schooten’s Theorem

Der Beweis, dass die magenta Strecke der Abbildung 4, also die erste gezeichnete Strecke, gleich lang ist wie die Gesamtlänge des Steiner-Netzes, geht induktiv mit van Schooten’s Theorem [1].

3.4 Topologie

Durch die Auswahl der jeweiligen Punktepaare für die aufzusetzenden Dreiecke wird die Topologie des Netzes festgelegt. Netze unterschiedlicher Topologien haben in der Regel unterschiedliche Gesamtlängen.

3.5 Dreiecke „nach innen“

Was geschieht, wenn wir die Dreiecke nach innen zeichnen?

Website

[1] Hans Walser: Van Schooten’s Theorem:

http://www.walser-h-m.ch/hans/Miniaturen/V/van_Schooten/van_Schooten.htm