Hans Walser, [20210627]

Spiralen mit rechtwinkligen Dreiecken

Anregung: Thomas Jahre, Aufg. 57-681

1 Worum geht es?

Wir bauen eckige Spiralen mit rechtwinkligen Dreiecken. Dabei treffen wir Beispiele von geometrischen, archimedischen, aber auch anderen Spiralen an.

2 Vorgehen

Wir wählen eine beliebige Folge b_n. Das Aussehen der Spirale hängt von dieser Folge ab. Im Beispiel der Abbildung 1 wurde b_n = 0.5n gewählt.

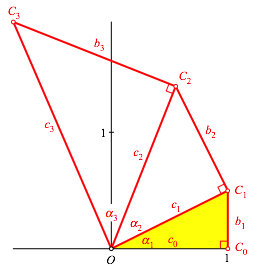
Abb. 1: Vorgehen

Wir beginnen nun mit einem rechtwinkligen Dreieck OC₀C₁ (Abb. 1). Das Dreieck hat die eine Kathete c₀ = 1 und die andere Kathete b₁. Die Hypotenuse bezeichnen wir mit c₁.

Diesem Dreieck setzen wir ein zweites rechtwinkliges Dreieck OC₁C₂ an gemäß Abbildung 1.

Und so weiter. So entsteht eine eckige Spirale.

3 Beispiele

3.1 Die Wurzelspirale

Wir wählen die konstante Folge b_n = 1 (Abb. 2).

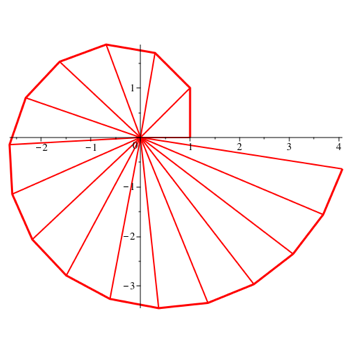
Abb. 2.1: Konstante Folge. 16 Dreiecke

Die Speichen sind der Reihe nach die Quadratwurzeln aus 1, 2, 3, ... , daher der Name der Spirale.

Für große Dreiecksanzahlen (Abb. 2.2) nähert sich die Spirale einer archimedischen Spirale (Walser 2004).

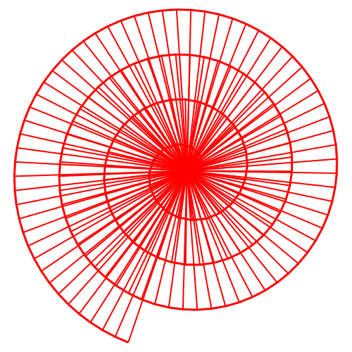
Abb. 2.2: Konstante Folge. 160 Dreiecke

3.2 Rechtwinklig gleichschenklige Dreiecke

Wir arbeiten mit der geometrischen Folge .

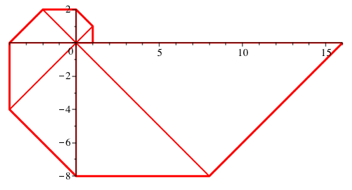
Abb. 3.1: Acht rechtwinklig gleichschenklige Dreiecke

Diese Spirale kann aus Origami-Papier durch Falten hergestellt werden.

Es handelt sich um eine eckige logarithmische Spirale. In der Abbildung 3.2 sind die ersten 96 Dreiecke gezeichnet. Wir sehen kaum einen Unterschied zur Spirale mit nur 8 Dreiecken der Abbildung 3.1.

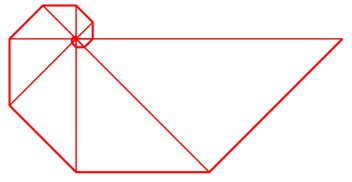
Abb. 3.2: 96 Dreiecke

3.3 Die natürlichen Zahlen

Wir arbeiten mit der arithmetischen Folge b_n = n.

Dieser Spiralentyp wird in der Aufgabe 57-681 von Thomas Jahre verwendet.

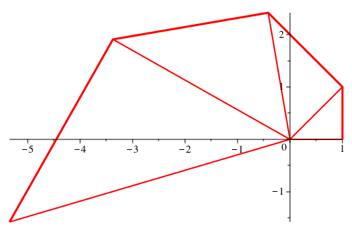
Abb. 4.1: Vier Dreiecke

Die Spirale wächst etwas stärker als die archimedische Spirale (Abb. 4.2).

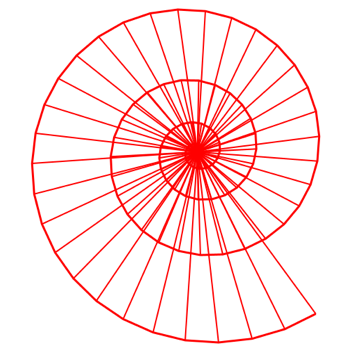
Abb. 4.2: 100 Dreiecke

3.4 Quadratzahlen

Wir verwenden die arithmetische Folge zweiter Ordnung b_n = n² (Abb. 5).

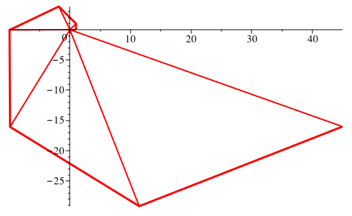
Abb. 5.1: Sechs Dreiecke

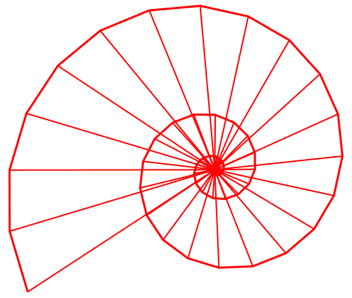
Abb. 65.2: 60 Dreiecke

3.5 Fibonacci Folge

Die musste ja kommen.

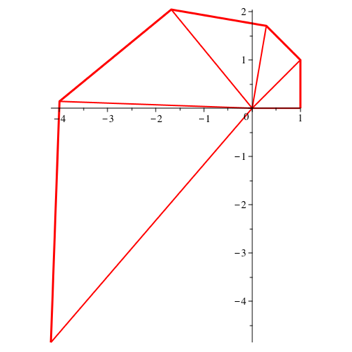
Abb. 6.1: Fünf Dreiecke

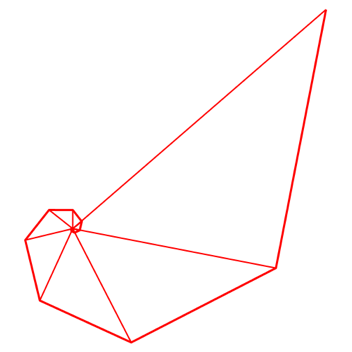
Abb. 6.2: 50 Dreiecke

3.6 Sinus-Folge

Bis jetzt haben wir immer mit monoton wachsenden Folgen (und einer konstanten Folge) gearbeitet.

Nun verwenden wir die Folge . Die geht auf und ab und ist immer wieder mal null. Das sieht zunächst ganz harmlos aus (Abb. 7.1).

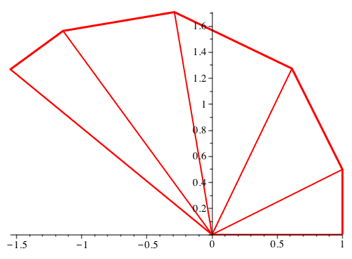
Abb. 7.1: Sechs Dreiecke. Wo ist das sechste Dreieck?

Anschließend kommen die negativen Sinuswerte zum Tragen. Die Spirale wird zurückgewendet (Abb. 7.2).

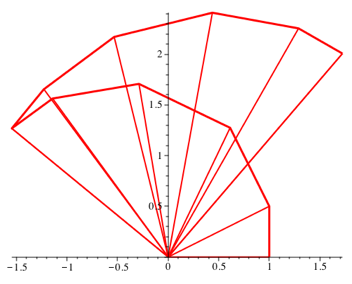
Abb. 7.2: Zwölf Dreiecke. Umkehrpunkt

Und so geht es hin und her (Abb. 7.3).

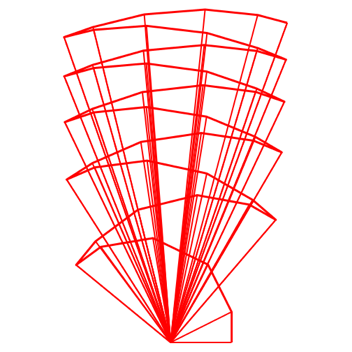
Abb. 7.3: 60 Dreiecke. Fächer

4 Pythagoras

Im Kontext von rechtwinkligen Dreiecken wird gerne über den Satz des Pythagoras gesprochen. Die Abbildung 8 zeigt die in unserem Kontext passende Version. Die Flächensumme der roten Quadrate ist gleich dem Flächeninhalt des großen blauen Quadrates über der letzten Speiche.

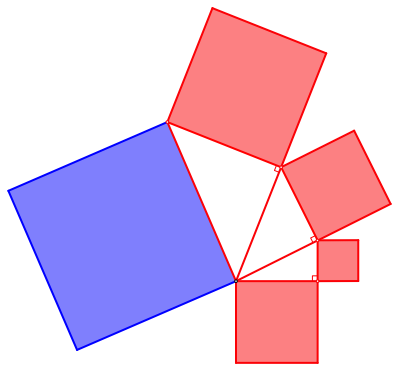
Abb. 8: Rot = blau

Literatur

Walser, Hans (2004): Pythagoras, eine archimedische Spirale und eine Approximation von π. Praxis der Mathematik (6/46), 2004, S. 287-288

Websites

Thomas Jahre: Aufgabe der Woche

https://www.schulmodell.eu/aufgabe-der-woche.html

Hans Walser: Eckige Spiralen

http://www.walser-h-m.ch/hans/Miniaturen/E/Eckige_Spiralen/Eckige_Spiralen.htm

Hans Walser: Falten einer Spirale

http://www.walser-h-m.ch/hans/Miniaturen/F/Falten_Spirale/Falten_Spirale.htm

Hans Walser: Spiralen und Schraubenlinien:

http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/Spiralen/index.html