Hans Walser, [20080126a]
Sierpinski, Cantor & Co
1
Das Sierpinski-Dreieck
Ein Uralt-Trick, das
Sierpinski-Dreieck zu generieren, besteht darin, dass man zunchst die drei
Eckpunkte ![]() ,
, ![]() ,
, ![]() des
gleichseitigen Dreieckes nimmt. Anschlie§end wird eine Punktfolge
des
gleichseitigen Dreieckes nimmt. Anschlie§end wird eine Punktfolge ![]() mit dem
Startpunkt
mit dem
Startpunkt ![]() rekursiv
definiert:
rekursiv
definiert:
![]()
Dabei ist r eine Zufallszahl aus {0, 1, 2}. Fr ![]() ergibt sich das
gewhnliche Sierpinski-Dreieck. Es sind 4000 Punkte gezeichnet.
ergibt sich das
gewhnliche Sierpinski-Dreieck. Es sind 4000 Punkte gezeichnet.

Problematisch bei
diesem Verfahren ist, dass wir viele Punkte brauchen (Speicher, Rechenzeit) und
dass es Probleme mit der Auflsung gibt.
Das Sierpinski-Dreieck
hat die fraktale Dimension ![]()
2
Varianten zum Sierpinski-Dreieck
Natrlich variieren wir
nun das ![]() .
.
Fr ![]() erhalten wir:
erhalten wir:
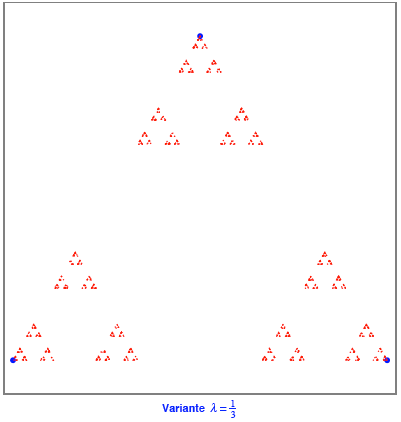
Das sieht noch ganz
ordentlich nach Fraktal aus. Fr die fraktale Dimension erhalten wir:
![]()
Das ist nicht eben
ãfraktalÒ.
Fr ![]() erhalten wir:
erhalten wir:
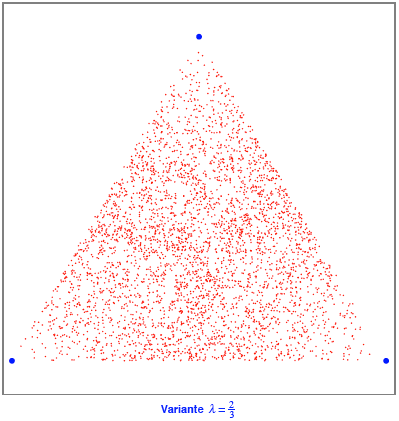
Die Punkte ![]() scheinen (fr
scheinen (fr ![]() ) berall dicht
im Dreieck zu liegen. Die fraktale Dimension ist 2.
) berall dicht
im Dreieck zu liegen. Die fraktale Dimension ist 2.
Fr ![]() gibt es auch
etwas Schnes.
gibt es auch
etwas Schnes.
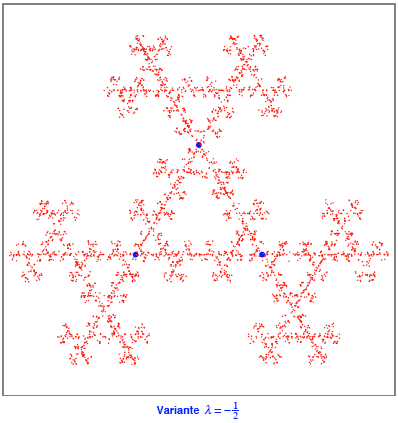
Fr ![]() reisen die
Punkte ab.
reisen die
Punkte ab.
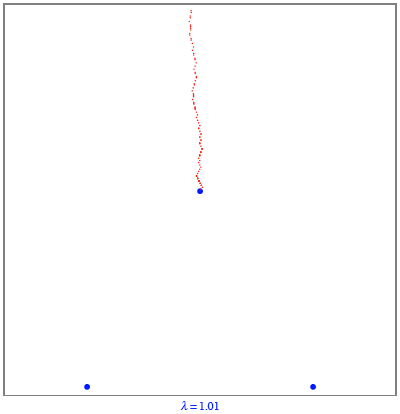
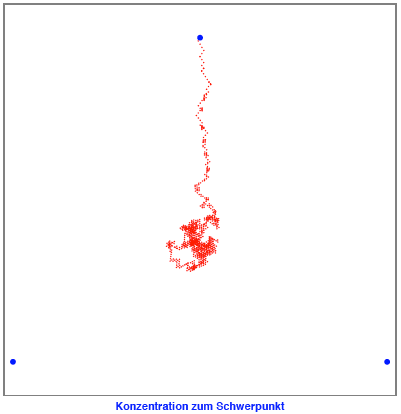
Fr ![]() haben die Punkte
den Schwerpunkt als Limes.
haben die Punkte
den Schwerpunkt als Limes.
3
Cantor
Wir knnen auch die
Eckenzahl variieren. Fr nur 2 Ecken und ![]() erhalten wir die
bliche Cantor-Menge (das so genannte Cantorsche Diskontinuum):
erhalten wir die
bliche Cantor-Menge (das so genannte Cantorsche Diskontinuum):

Die Cantor-Menge hat
die fraktale Dimension ![]() .
.
Fr ![]() (goldener
Schnitt) erhalten wir die unendlich fortgesetzte Unterteilung im goldenen
Schnitt.
(goldener
Schnitt) erhalten wir die unendlich fortgesetzte Unterteilung im goldenen
Schnitt.

4
Viereck
Das Viereck ist
langweilig.
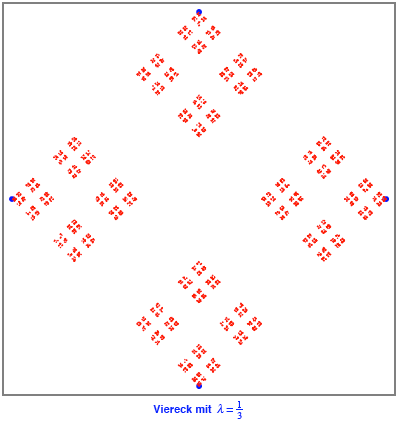
Die fraktale Dimension
ist ![]() , das Doppelte der fraktalen Dimension der Cantor-Menge.
, das Doppelte der fraktalen Dimension der Cantor-Menge.
5
Fnfeck
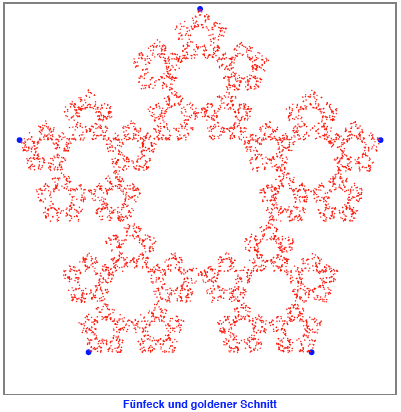
Beim Fnfeck fahren wir
gleich mit dem goldenen Schnitt los: ![]()
6
Sechseck
Beim Sechseck arbeiten
wir mit ![]() .
.
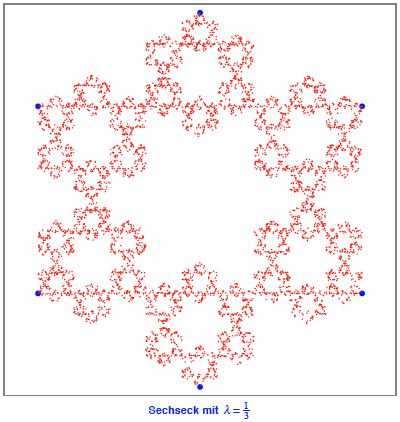
Wir erkennen im Zentrum
die Kochsche Schneeflocke.
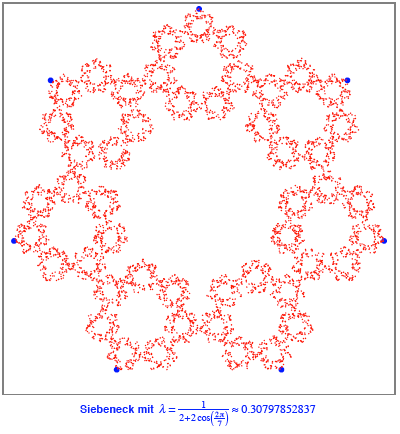
7
Siebeneck
Beim Siebeneck versuchen
wir es mit ![]() .
.
8
Software
Die Bilder wurden mit
MuPAD gezeichnet. Nachfolgend das Programm fr das Sierpinski-Dreieck.
n:=3:
m:=4000:
lambda:=0.5:
delta:=PI/2:
for k from 0 to n-1 do
P[k]:=cos(k*2*PI/n+delta)+I*sin(k*2*PI/n+delta):
end_for:
Q[0]:=P[0]:
r:=random(0..n-1):
for j from 1 to m do
Q[j]:=lambda*Q[j-1]+(1-lambda)*P[r()]:
end_for:
Punkt:=k->plot::Point2d([Re(P[k]), Im(P[k])], PointSize=2,
PointColor=[0,0,1]):
Qunkt:=j->plot::Point2d([Re(Q[j]), Im(Q[j])], PointSize=0.5,
PointColor=[1,0,0]):
plot(Punkt(k)$k=0..n-1, Qunkt(j)$j=1..m, Scaling=Constrained,
Axes=None, Width=140, Height=140, BorderWidth=1/4*unit::mm):