Hans Walser, [20070130a]

Fortlaufende Spiegelung an den Seiten eines Sehnenvieleckes mit gerader Eckenzahl

1 Worum es geht

In einem Vieleck mit Umkreis (Sehnenvieleck) wird fortlaufend an den Seiten gespiegelt. Bei gerader Eckenzahl entsteht eine Translation, bei ungerader Eckenzahl eine Schubspiegelung.

Stichworte:

Evolvente, Geradenspiegelungen, Parität, Peripheriewinkel, Regelmäßige Vielecke, Rotationen, Sehnenviereck, Symmetrie, Translationen, Zusammensetzung von Abbildungen.

2 Theorem

Es seien die Seiten eines Sehnenvieleckes mit gerader Eckenzahl. Dann ist

eine Translation.

3 Beispiele

Für ist und .

Für ergibt sich ein Sehnenviereck. Die Sehnen sind verlängert gezeichnet, um die Spiegelungen besser sichtbar zu machen.

Sehnenviereck

Das allgemeine Viereck liefert ein Gegenbeispiel.

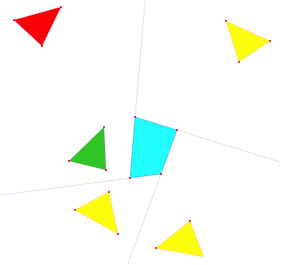
Gegenbeispiel

Für ergibt sich ein Sehnensechseck.

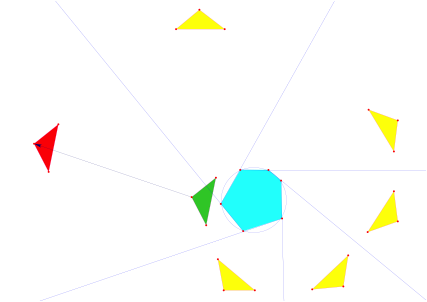
Sehnensechseck

Noch für das Sehnenachteck.

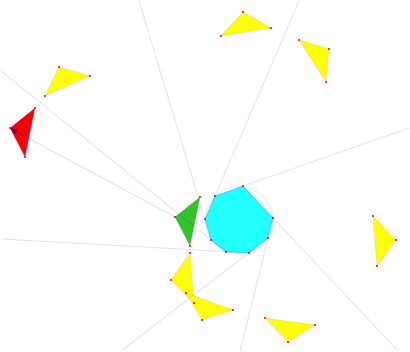
Sehnenachteck

4 Beweisansatz

Für das Sehnenviereck ist die Sache einfach. Es sei der Außenwinkel und der Eckpunkt zwischen und der Folgeseite . Dann zerfällt in zwei Rotationen, nämlich und . Nun hat aber das Sehnenviereck die Winkeleigenschaft: (und auch ). Somit ist die Abbildung insgesamt eine Rotation (mit einem unbekannten Drehzentrum) und dem totalen Drehwinkel , also eine Translation.

5 Winkeleigenschaft des Sehnenvieleckes mit gerader Eckenzahl

Die Frage ist nun, ob sich die Winkeleigenschaft des Sehnenviereckes geeignet verallgemeinern lässt, um die Feststellung über die Abbildung zu beweisen.

Dazu exemplarisch und experimentell ein Sehnensechseck.

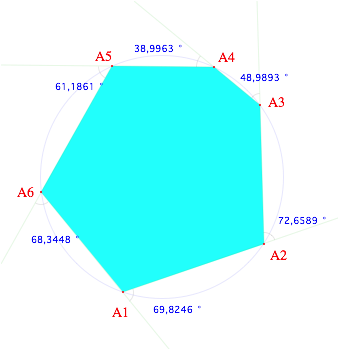
Sehnensechseck mit Außenwinkeln

Im Beispiel ist

Da die Auenwinkelsumme 360° ist, haben wir auch .

Wir vermuten:

Im Sehnenvieleck mit 2n Ecken gilt die Winkelbeziehung:

5.1 Induktionsbeweis

Für (Sehnenviereck) gilt die Beziehung.

Induktionsannahme: Die Beziehung gelte für Eckenzahlen kleiner als 2n. Wir zerlegen nun das Sehnenvieleck mit der Diagonalen in das Sehnenvieleck und das Sehnenviereck gemäß Figur.

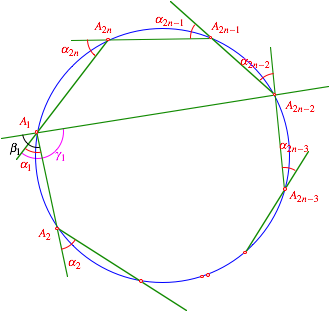
Beweisfigur

Dann ist nach Induktionsvoraussetzung

und

.

Addition liefert

.

Nun ist aber . Damit erhalten wir

.

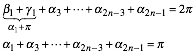Wegen der Außenwinkelsumme ist dann aber auch:

Damit ist die Vermutung über die Winkeleigenschaft im Sehnenviereck mit gerader Eckenzahl bewiesen.

5.2 Dynamischer Beweis

Die Winkelbeziehung lässt sich auch durch eine dynamische Überlegung nachweisen.

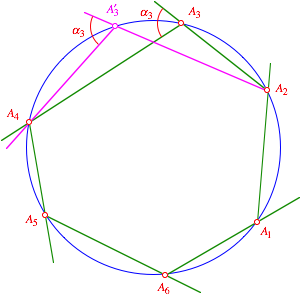
Bewegen eines Punktes

Wenn wir einen Punkte mit zum Beispiel ungeradem Index auf dem Kreis bewegen, ändert der zugehörige Außenwinkel nicht (Peripheriewinkel). Die übrigen Winkel mit ungeradem Index bleiben unangetastet. Damit bleibt bei diesem Prozess die Summe für die ungeraden Indizes unverändert und damit auch die Summe für die geraden Indizes, obwohl die beiden zum bewegten Punkt benachbarten Winkel verändert werden, aber eben gegengleich.

Nun bewegen wir die Punkte des 2n-Eckes, bis wir ein regelmäßiges 2n-Eck haben. Dort ist die Winkeleigenschaft aus Symmetriegründen erfüllt. Damit gilt sie auch für das unregelmäßige 2n-Eck. Ich finde diesen Beweis schöner als den Induktionsbeweis.

6 Beweis der Abbildungseigenschaft

Wir zerlegen in n Paare . Das macht insgesamt eine Rotation um , also eine Translation.

7 Ungerade Eckenzahl

Für ein Sehnenvieleck mit ungerader Eckenzahl ist eine Schubspiegelung und erst eine Translation. Wir brauchen zwei Umgänge.

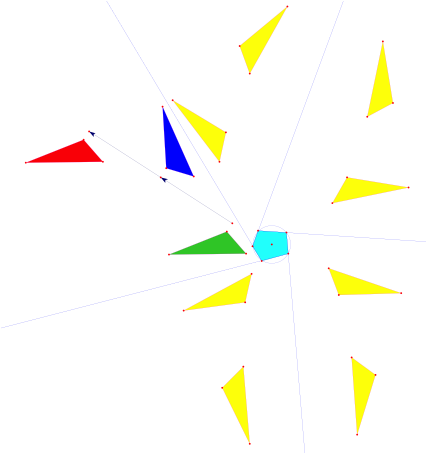
Sehnenfünfeck

8 Regelmäßige Vielecke mit gerader Eckenzahl

Beim allgemeinen Sehnenviereck mit gerader Eckenzahl ist der Translationsvektor von der Verteilung der Eckpunkte auf dem Umkreis abhängig. Bei regelmäßigen Vielecken hängt der Translationsvektor nur von der Eckenzahl 2n ab. Bei regelmäßigen 2n-Ecken haben wir einen konstanten Außenwinkel .

Im folgenden sei der Umkreis jeweils der Einheitskreis. Dann gilt:

Im regelmäßigen 2n-Eck ist

mit

Beweis: Wir fassen die Spiegelungen paarweise zusammen:

Damit ist:

Der Drehwinkel ist der Außenwinkel des regelmäßigen n-Eckes , das entsteht, wenn wir aus dem ursprünglichen 2n-Eck jede zweite Ecke auswählen.

Nun bilden wir exemplarisch einen Punkt ab; da wir schon wissen, dass die Gesamtabbildung eine Translation ist, genügt das, um den Translationsvektor zu bestimmen. Wir wählen den Urbildpunkt .

Wenn wir „durchspiegeln“, erhalten wir mit .

Wenn wir „durchdrehen“, erhalten wir mit .

Die folgende Figur zeigt dieses „Durchdrehen“ für den Fall , also dem regelmäßigen Zehneck mit dem regelmäßigen Fünfeck als Hilfsfigur.

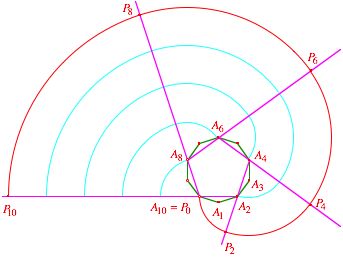
Überlegungsfigur

Bei der ersten Drehung (um ) erhalten wir . Bei der Drehung um erhalten wir und so weiter und so fort, und schließlich bei der letzten Drehung (um ) den gesuchten Endpunkt . Die Drehradien nehmen bei jeder Drehung um die Seitenlänge des regelmäßigen n-Eckes zu. Somit erhalten wir :

Die Länge des Translationsvektors ist gleich dem Umfang des regelmäßigen n-Eckes . Der Translationsvektor kann also nicht beliebig lang werden, vielmehr gilt:

Bei den in der Überlegungsfigur eingezeichneten Bahnkurven handelt es sich um so genannte Wälzkurven oder Evolventen des regelmäßigen n-Eckes .

Die folgende Figur zeigt die Evolvente des Kreises.

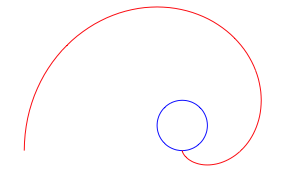
Evolvente