Hans Walser, [20160714]

Runde Wellenlinien

1 Worum geht es?

Es werden zirkulär angeordnete Wellenlinien besprochen.

2 Ringe und Flächen

Wir zeichnen konzentrische Kreise mit den Radien 2, 4, 6, 8, 10, ... (Abb. 1). So entstehen Kreisringe der Breite 2.

Abb. 1: Kreisringe

Die Kreisringe haben von innen nach außen die linear zunehmenden Flächeninhalte 4π, 12π, 20π, 28π, 36π, ... . Wir können sie also unterteilen in Ringsektoren mit dem konstanten Flächeninhalt 4π (Abb. 2).

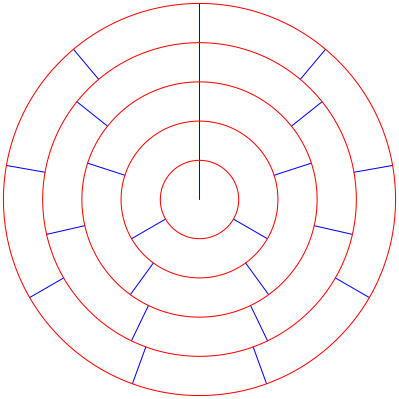
Abb. 2: Flächengleiche Rinngsektoren

3 Treppengiebel

Die Abbildung 3 zeigt einen Treppengiebel, der aus Rechtecken der Länge 2π und der Höhe 2 aufgebaut ist.

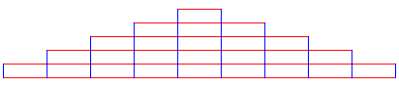
Abb. 3: Treppengiebel

Wir sehen, dass die Abbildung 2 sozusagen die aufgewickelte Form der Abbildung 3 ist.

4 Das Rechteck

Ein Rechteck der Länge 2π und der Höhe 2 oder allgemein ein Rechteck mit gleichen Seitenverhältnissen kommt in verschiedenen Zusammenhängen vor.

So passt etwa die flächenverhältnistreue normalachsige Weltkarte (cylindrical equal area) nach Archimedes / Lambert in ein solches Rechteck (Abb. 4).

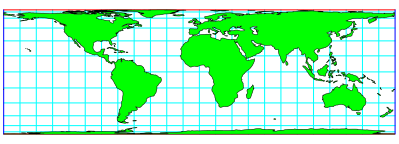
Abb. 4: Flächenverhältnistreue Weltkarte

Aber ebenso passt eine gewöhnliche Kosinuskurve in dieses Rechteck (Abb. 5).

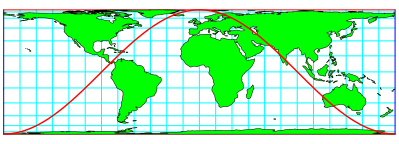
Abb. 5: Kosinuskurve

Die Kosinuskurve verläuft durch Schnittpunkte von Meridianen und Breitenkreisen der flächenverhältnistreuen Karte. Man kann sich überlegen, warum das so sein muss.

5 Kosinuskurven

Die Abbildung 6 zeigt Kosinuskurven im Treppengiebel der Abbildung 3.

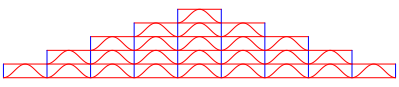
Abb. 6: Kosinuskurven im Treppengiebel

6 Wellenlinien in Ringen

Nun wickeln wir den Treppengiebel mitsamt den Kosinuskurven zur Kreisfigur gemäß Abbildung 2 auf (Abb. 7). So erhalten wir runde Wellenlinien.

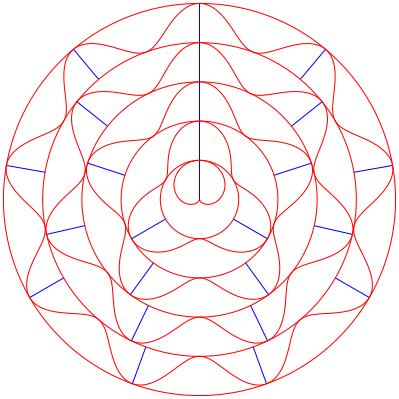
Abb. 7: Runde Wellenlinien

Die Abbildung 8 zeigt mehr Ringe. Die Unterteilungen in flächengleiche Ringsektoren sind aber weggelassen.

Abb. 8: Mehr runde Wellenlinien

Die Gesamtfigur hat eine senkrechte Symmetrieachse.

7 Andere Wellenlängen

Wenn wir die Frequenz verdoppeln, halbiert sich die Wellenlänge (Abb. 9). Wir haben jetzt eine senkrechte und eine waagereche Symmetrieachse.

Abb. 9: Zwei Symmetrieachsen

Die Abbildungen 10 bis 13 zeigen Beispiele mit 3 bis 6 Symmetrieachsen.

Abb. 10: Drei Symmetrieachsen

Abb. 11: Vier Symmetrieachsen

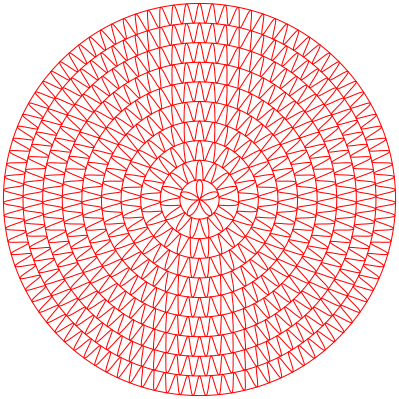
Abb. 12: Fünf Symmetrieachsen

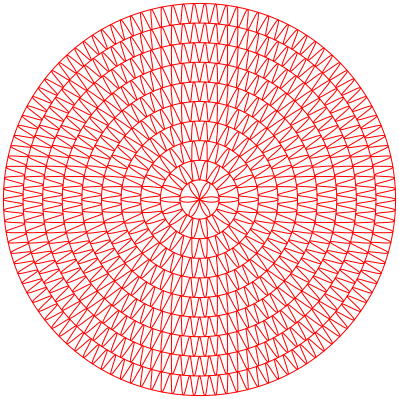
Abb. 13: Sechs Symmetrieachsen

8 Zentrumsfiguren

Die Abbildungen 14 bis 19 zeigen die Zentrumsfiguren der Abbildungen 8 bis 13, also die Figuren im innersten Kreis.

Im Beispiel der Abbildung 8 erhalten wir die so genannte Kardioide (Abb. 14). Die Kardioide hat die ganzzahlige Bogenlänge 8.

Abb. 14: Kardioide

Im Beispiel der Abbildung 9 erhalten wir ein Doppel-Ei (Abb. 15). Die Kurve hat die Gesamtlänge 11.04138399, also kein „schönes“ Resultat.

Abb. 15: Doppel-Ei

Aus den Abbildungen 10 bis 13 ergeben sich die Kleeblätter oder Rosetten der Abbildungen 16 bis 19.

Abb. 16: Kleeblatt

Abb. 17: Kleeblatt mit vier Blättern

Abb. 18: Fünf Blätter

Abb. 19: Sechs Blätter

Websites

Cylindrical equal area (17. 07. 2016)

http://swai.ethz.ch/swaie/MapProjector/MapProjector.de.html