Hans Walser, [20160928]

Rhombenfiguren

Anregung: Heinz Klaus Strick, Leverkusen

1     Worum geht es?

Eine klassische Figur mit Rhomben wir variiert und verrŠumlicht.

2     Der Klassiker

Die Abbildung 1 zeigt exemplarisch die klassische Figur.

Abb. 1: Rhombenfigur

Der Umriss ist ein regelmŠ§iges 14-Eck. Die folgenden †berlegungen gelten aber auch fŸr andere gerade Eckenzahlen.

Die SeitenlŠnge der Rhomben setzen wir 1. Das regelmŠ§ige 14-Eck hat die SeitenlŠnge 2. Wir werden spŠter sehen, was sich dahinter verbirgt.

Die Abbildung 2 zeigt einen ma§stŠblichen Ausschnitt.

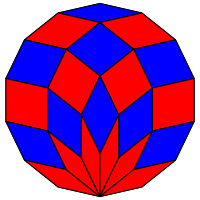
Abb. 2: Ausschnitt

Der Ausschnitt ist ebenfalls ein regelmŠ§iges 14-Ecke, aber nur noch mit der SeitenlŠnge 1.

3     Variationen

Der Ausschnitt kann in der ursprŸnglichen Figur um Vielfache von  gedreht werden. Die Abbildungen 3 und 4 zeigen zwei Beispiele.

Abb. 3: Andere Anordnung der Rhomben

Abb. 4: Achsialsymmetrische Anordnung

In der Abbildung 5 sehen wir sogar zwei Verdrehungen. ZusŠtzlich sind die Rhomben anders koloriert.

Abb. 5: Spiralen

4     Im Raum

Wir versuchen, die Figur der Abbildung 1 zu verrŠumlichen.

Wir denken uns den Mittelpunkt auf dem Niveau 0.

Die Eckpunkte im innersten Ring heben wir auf das Niveau 1 an. Dadurch werden die Rhombenkanten auf  verlŠngert. Die Rhombenkanten haben gegenŸber der Bodenebene (x,y-Ebene) die Steigung 1, also  den Winkel 45¡.

Die Eckpunkte des zweitinnersten Ringes kommen dann automatisch auf des Niveau 2, da die Rhomben ja eben bleiben sollen.

Die Eckpunkte des i-ten Ringes kommen auf das Niveau i.

Wir illustrieren die entstehende Figur schrittweise, die Abbildung 6 zeigt den Start. In der x,y-Ebene ist als Referenz die zweidimensionale Figur der Abbildung 1 eingezeichnet.

Abb. 6: Auf in den Raum

Die Abbildung 7 zeigt die beiden nŠchsten Schritte.

 

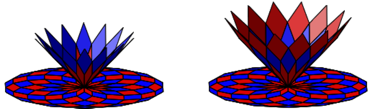
Abb. 7: Die beiden nŠchsten Schritte

Die Abbildung 8 zeigt die beiden nachfolgenden Schritte.

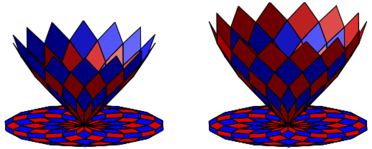
Abb. 8: Schritte 4 und 5

Wir sehen jetzt, dass sich die FlŠche einzukrŸmmen beginnt. Es entwickelt sich keine kegelfšrmige Figur, obwohl das mit dem linearen Wachstum der Eckpunkthšhen vielleicht zu erwarten war. Der Grund liegt darin, dass die radialen AbstŠnde der Eckpunkte unterlinear zunehmen.

Die Abbildung 9 zeigt links den letzten Schritt und rechts den nŠchsten. Das ist natŸrlich sprachlich unlogisch. Nach dem letzten Schritt gibt es wie nach dem jŸngsten Tag keinen nŠchsten. Das ist erklŠrungsbedŸrftig.

Nach diesem ãletztenÒ Schritt haben wir oben einen Kranz mit blauen Rhomben. Sie entsprechen den Šu§ersten Rhomben in der ebenen Figur. Also ultimativ.

Wir kšnnen aber im Raum auf die Zickzackkanten oben einen weiteren Kranz von Rhomben aufsetzen (rot im nŠchsten Schritt). Diese Rhomben stehen genau senkrecht und erscheinen in der ebenen Figur nur noch als Doppelstrecken. Das erklŠrt auch, warum das 14-Eck der Abbildung 1 Kanten der LŠnge 2 hat. Diese neuen roten Rhomben sind Ÿbrigens exakte Quadrate. Das ist so die Situation, wo man mal zu Recht sagen kann, Mathematik sei schšn.

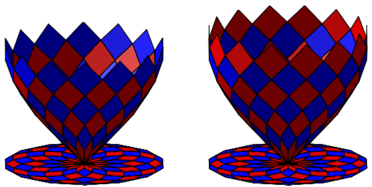
Abb. 9: Der letzte Schritt und dann der nŠchste

Was hindert uns daran, auf den obersten Kranz noch einen draufzusetzen? (Abb. 10)

Abb. 10: Die beiden nŠchsten Schritte

Wir sehen, wie die Sache weiterlŠuft. Die Abbildung 11 zeigt die beiden nŠchsten Schritte.

Abb. 11: Die beiden nŠchsten Schritte

Die Abbildung 12 schlie§lich zeigt das Finale.

Abb. 12: Finale

Allerdings arbeitet das System unverdrossen weiter (Abb. 13).

Abb. 13: Das Leben geht weiter

Wir ahnen, was kommt (Abb. 14).

Abb. 14: Zweite Runde

Die Sache wird periodisch.

Die geschlossene Figur der Abbildung 12 approximiert eine Sinusspindel (sinusoidale Spindel) (Abb. 15). Die Sinusspindel hat einen Sinusbogen als Meridian.

Abb. 15: Sinusspindel

Lehrer LŠmpel: Berechne das Volumen der Sinusspindel.

5     Koordinaten und Formeln

Die folgenden Formeln beziehen sich auf die Figur der Abbildung 1. Es werden die Polarkoordinaten der Eckpunkte der Rhomben bestimmt.

Mit n bezeichnen wir die Eckenzahl des regelmŠ§igen Vieleckes.

Exemplarisch ist n = 14.

Weiter sei . Dieser Winkel ist also der halbe spitze Winkel der kleinesten Rhomben.

FŸr die PolarabstŠnde (Index i) der Eckpunkte erhalten wir die Rekursion:

 

                                                                                                (1)

 

 

Explizit hei§t das:

 

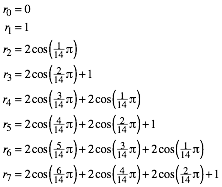                                                               (2)

 

 

 

 

 

 

 

Das sind die tatsŠchlich benštigten Radien. Wenn wir mit der Rekursion (1) weiterrechnen, ergibt sich:

 

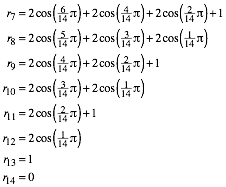                                                               (3)

 

 

 

 

 

 

Wir sehen die GesetzmŠ§igkeit.

FŸr die Polarwinkel (Index j) gilt:

 

                                                                                                   (4)

 

Somit erhalten wir fŸr die Eckpunkte die Polarkoordinaten:

 

                                                                                                                 (5)

 

Die Abbildung 16 zeigt die Kontrollzeichnung.

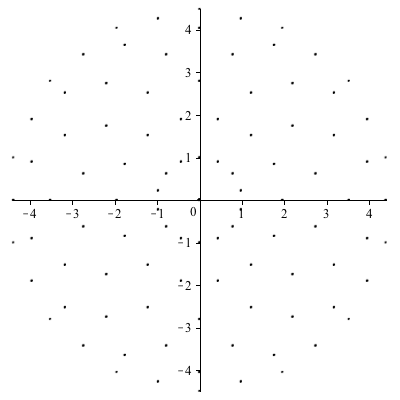
Abb. 16: Kontrollzeichnung der Eckpunkte

Der Rhombus Ri,j hat die Eckpunkte:

 

              (6)

 

Im rŠumlichen Fall haben die Eckpunkte die Zylinderkoordinaten:

 

                                                                                                               (7)