Hans Walser, [20110920a]

Reuleaux-Dreiecke

Anregung: J. R., K.-L.

1        Ausgangslage

Die Abbildung zeigt ein Reuleaux-Dreieck.

 

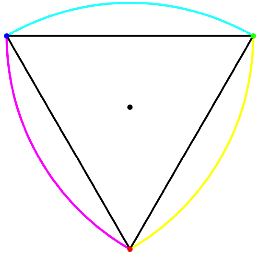
Reuleaux-Dreieck

 

Es entsteht aus einem gleichseitigen Dreieck, das durch Kreisbogen ergŠnzt wird. Das Reuleaux-Dreieck hat einen konstanten Durchmesser, ist also wie der Kreis ein ãGleichdickÒ. Zylinder (Walzen) mit einem Reuleaux-Dreieck als Querschnitt kšnnen also zum Abrollen eines Rollgutes benutzt werden, wobei der Abstand des Rollgutes vom Boden konstant ist.

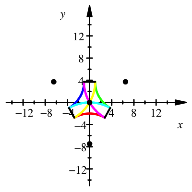
Der Mittelpunkt des Reuleaux-Dreieckes (mit Mittelpunkt ist der FlŠchenschwerpunkt gemeint, oder gleichbedeutend das Zentrum der dreistrahligen Drehsymmetrie) mit dem Durchmesser 2 beschreibt beim Abrollen folgende Kurve.

 

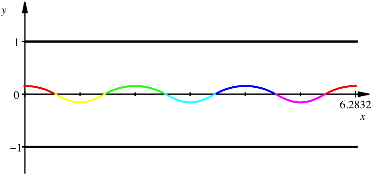
Rollkurve

 

In der Abbildung ist die untere schwarze Linie der Boden, die obere schwarze Linie die Unterkante des Rollgutes.

Die Mittelpunkts-Rollkurve setzt sich aus Kreisbšgen (rot, grŸn, blau) und verkŸrzten Zykloidenbšgen (gelb, cyan, magenta) zusammen. Der rote Kreisbogen entsteht durch Abrollen im den roten Punkt, der gelbe verkŸrzte Zykloidenbogen durch Abrollen auf dem gelben Kreisbogen des Reuleaux-Dreieckes. Entsprechend die Ÿbrigen Teile der Rollkurve.

Die folgende Abbildung zeigt die roten Kreisbogen zum Kreis ergŠnzt und ebenso die gelben verkŸrzten Zykloidenbogen zur verkŸrzten Zykloide ergŠnzt, das Ganze Ÿber drei PeriodenlŠngen.

 

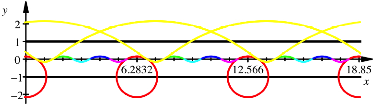
ErgŠnzung der Bšgen

 

Wir sehen, dass ein Zykloidenbogen jeweils erst nach einer Doppelperiode wieder aktiv wird.

2        Fragen und Probleme

a) Die Rollkurve ist also nicht symmetrisch. Das ist schwer einzusehen, da doch Boden und Unterkante des Rollgutes vertauscht werden kšnnen.

b) Zudem ist es so, dass die Kreisbšgen mit Zirkel und Lineal gezeichnet werden kšnnen, die Zykloidenbšgen nicht. (Letzteres folgt daraus, dass bei der gewšhnlichen Zykloide die Spannweite dem Umfang des abgerollten Kreises entspricht, der Kreisumfang kann aber nicht mit Zirkel und Lineal gezeichnet werden).

Die Frage b) kann sofort beantwortet werden: Auch die Kreise kšnnen nicht mit Zirkel und Lineal gezeichnet werden. — Wie bitte? — Die Mittelpunkte der roten Kreise zum Beispiel haben einen horizontalen Versatz von , das kann nicht mit Zirkel und Lineal gezeichnet werden. Wir kšnnen also den rot-grŸn-blauen Teil der Rollkurve zwar bogenweise mit Zirkel und Lineal zeichnen, nicht aber als Gesamtheit. — Wir werden im folgenden sehen, dass die Kreis SonderfŠlle von verlŠngerten Zykloiden sind.

3        Zykloiden

Auf einem Rad mit Radius r bringen wir einen Zeichenstift an, der vom Radmittelpunkt den Abstand s hat. Wir das Rad abgerollt, beschreibt der Zeichenstift eine Zykloide, und zwar:

 

 

 

 

Die Abbildung zeigt rot die gewšhnliche Zykloide, grŸn die verkŸrze Zykloide mit  und blau die verlŠngerte Zykloide mit . Es sind drei PeriodenlŠngen gezeichnet.

 

Gewšhnliche, verkŸrzte und verlŠngerte Zykloide

 

Die gewšhnliche Zykloide hat Umkehrpunkte auf dem Boden. Die verkŸrzte Zykloide berŸhrt den Boden nicht. Die verlŠngerte Zykloide hat Schlaufen, die unterhalb des Bodens reiche. Eine verlŠngerte Zykloide mit  ist ein Kreis mit Radius s.

4        Verallgemeinertes Reuleaux-Dreieck

Die folgenden Reuleaux-Dreiecke haben alle den Durchmesser 2 und damit den Umfang . Mit dem Parameter p bezeichnen wir den Radius der drei kleinen Bšgen (rot, grŸn, blau). In der folgenden Abbildung ist .

 

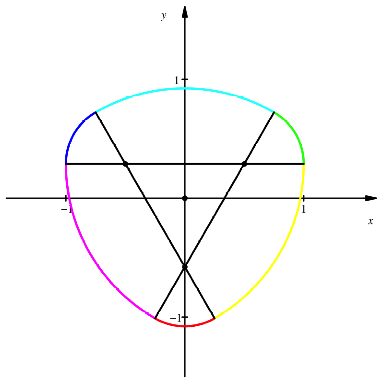
Verallgemeinertes Reuleaux-Dreieck mit

 

FŸr  erhalten wir das gewšhnliche Reuleaux-Dreieck, fŸr  den Kreis.

 

 

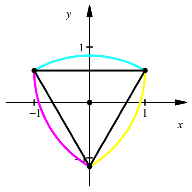
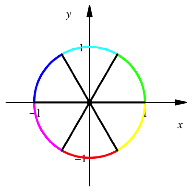
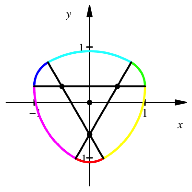
Gewšhnliches Reuleaux-Dreieck und Kreis

 

FŸr  erhalten wir das Marktbreit-Dreieck. Die kleinen Kreisbšgen (rot, grŸn, blau) sind Teil der kanonischen Kreisrosette.

 

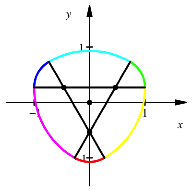
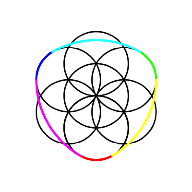
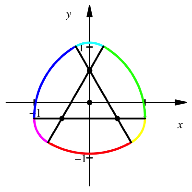
Marktbreit-Dreieck. Kreisrosette

 

FŸr  erhalten wir im Prinzip dasselbe wie fŸr , aber mit vertauschten Farben.

 

 

 und

 

FŸr  ergibt sich ein nicht konvexes Gleichdick. Der konstante Durchmesser muss als Innenma§ mit den ãkleinenÒ Messschenkeln der Schublehre (Messschieber) verifiziert werden.

 

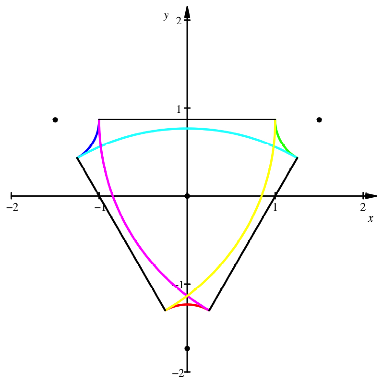
Nicht konvexes Gleichdick fŸr

 

Bei stark negativem p erkennen wir, dass das Reuleaux-Dreieck ein Mšbius-Band (konstanter Breite) ist. Die folgende Abbildung zeigt den Fall .

 

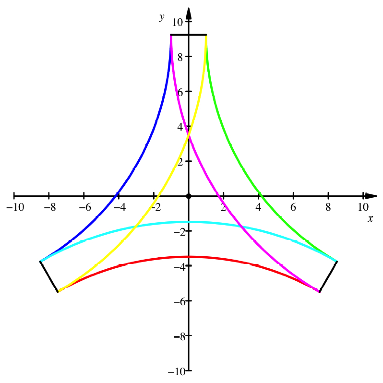
Mšbiusband ()

 

FŸr  lassen sich die gro§en Kreisbšgen (cyan, magenta, gelb) in die kanonische Kreisrosette einbetten.

 

 

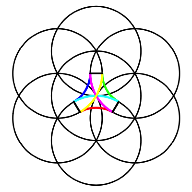
Nochmals Kreisrosette

 

So weit so gut. Und nun die Mittelpunkts-Rollkurven. Vorerst aber noch eine Zwischenbemerkung.

5        Drehgeschwindigkeiten

Wir denken uns eine Walze mit dem Einheitskreis als Querschnitt sowie verschiedene Walzen mit allgemeinen Reuleaux-Dreiecken mit gleichem Durchmesser 2 als Querschnitt. †ber diese (parallel ausgerichteten) Walzen legen wir eine Platte und rollen so ab, dass sich der Einheitskreis gleichmŠ§ig dreht. Die Frage ist, ob sich auch die Reuleaux-Dreiecke gleichmŠ§ig drehen.

Die Frage ist nicht  trivial. Es ist ja auch zum Beispiel so, dass sich bei einem angewinkelten Kardangelenk eine gleichmŠ§ige Drehbewegung nicht gleichmŠ§ig ŸbertrŠgt.

Die Frage konnte ich nur differenziell angehen. Wenn sich der Einheitskreis um  dreht, bewegt sich die Platte um . Es sei nun  die Drehgeschwindigkeit eines Reuleaux-Dreiecks mit dem Parameter p. Zum kleinen Radius p gehšrt der gro§e Gegenradius . Somit ist:

Es ist also ; die beiden Drehgeschwindigkeiten sind gleich. Wir kšnnten daher den fŸr den Einheitskreis gŸltigen Drehparameter t auch fŸr die Reuleaux-Dreiecke verwenden.

6        Mittelpunkts-Rollkurven

Die folgende Abbildung zeigt die Mittelpunkts-Rollkurve fŸr . Es sind zwei Perioden dargestellt.

 

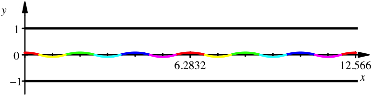
Mittelpunkts-Rollkurve fŸr

 

In der folgenden Abbildung sind der erste rote Bogen und der erste gelbe Bogen in extenso gezeichnet.

 

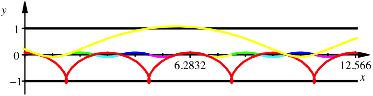
Bogen in extenso fŸr

 

Die rote Kurve ist eine (knapp) verlŠngerte Zykloide, die gelbe Kurve eine verkŸrzte Zykloide. Erschreckend sind aber die unterschiedlichen PeriodenlŠngen. Die rote Kurve hat die PeriodenlŠnge , die gelbe Kurve die PeriodenlŠnge .

Dazu ein zweites Beispiel, nŠmlich .

 

 

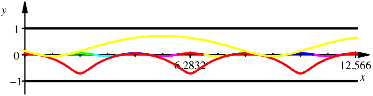
Wir haben fŸr die rote Kurve die PeriodenlŠnge , fŸr die gelbe Kurve die PeriodenlŠnge . Beide Kurven sind verkŸrzte Zykloiden.

6.1      PeriodenlŠngen

FŸr die PeriodenlŠngen gilt:

Das ergibt sich daraus, dass p und  die Radradien der beiden Zykloiden sind.

Wenn p irrational ist, wird eine Zykloide keinen weiteren Bogen mehr abdecken.

6.2      Marktbreit-Dreieck

FŸr  erhalten wir das Marktbreit-Dreieck. Die rote Kurve seiner Mittelpunkts-Rollkurve ist eine exakte gewšhnliche Zykloide. Das ergibt sich daraus, dass der Mittelpunkt des Dreiecks auf den kleinen Kreisen liegt. Es ist also der Stiftradius gleich dem Radradius. Die Kurven passen genau in den Zwischenraum zwischen Boden und Rollgutunterkante.

 

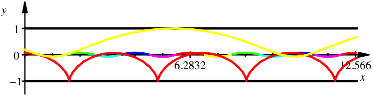
Gewšhnliche Zykloide

 

6.3      Nicht konvexes Reuleaux-Dreieck

Wie kann das Abrollen eines nicht konvexen Reuleaux-Dreiecks mechanisch realisiert werden?

Die folgende Figur zeigt die Mittelpunkts-Rollkurve fŸr den Fall . Wir haben die PeriodenlŠngen  fŸr die rote Kurve und  fŸr die gelbe Kurve.

 

 

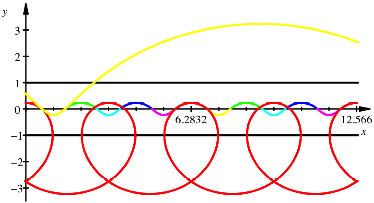
7        Bewegen des Bezugssystems

7.1      Ortsfest

Bis jetzt hatten wir alles in einem ortsfesten (bodenfesten) Koordinatensystem beschrieben. Als Illustration nochmals den Fall des gewšhnlichen Reuleaux-Dreiecks im ortsfesten Koordinatensystem. Wir haben unten Kreise und oben verkŸrzte Zykloiden.

 

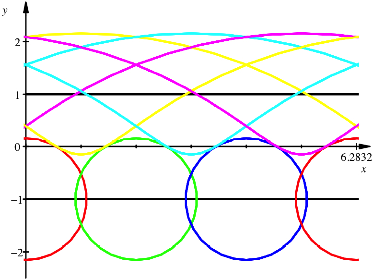
Ortsfest

 

Nun lassen wir das Koordinatensystem mit der Geschwindigkeit  nach rechts wandern.

Vorstellung: Wir bewegen eine Kamera.

Durch das Bewegen der Kamera wird die Vorschubgeschwindigkeit bei den Zykloiden verŠndert. Geometrisch hei§t das, dass der Radradius verŠndert wird und die Abrollgerade entsprechend verschoben. Die Kurven bleiben also nach wie vor Zykloiden.

7.2      Vom Schiff aus

FŸr  bewegt sich die Kamera mit dem Rollgut. FŸr das gewšhnliche Reuleaux-Dreieck sehen wir ãvom Schiff ausÒ nun oben die Kreise (magenta, cyan, gelb) und unten die verkŸrzten Zykloiden.

 

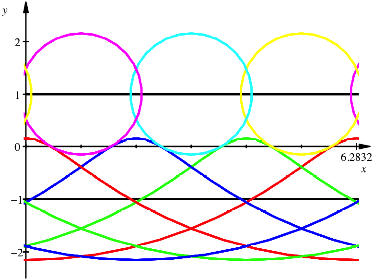
Vom Schiff aus

 

7.3      Der Mittelpunkt im Fokus

FŸr  haben wir den Mittelpunkt des Reuleaux-Dreiecks im Fokus. Die folgende Abbildung zeigt die Situation fŸr das gewšhnliche Reuleaux-Dreieck. Die drei oberen und die drei unteren Kurven Ÿberlagern sich. Sie sind symmetrisch. 

 

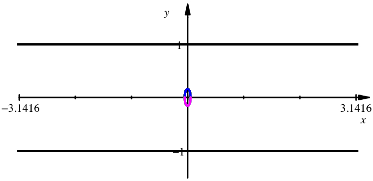
Bewegung des Mittelpunktes

 

Gezoomt (Faktor 10) erhalten wir die folgende Abbildung.

 

 

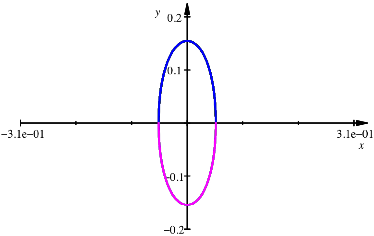
Bewegung des Mittelpunktes

 

Der Mittelpunkt des Reuleaux-Dreieckes eiert also nicht nur auf und ab, sondern im Vergleich mit der gleichmŠ§igen Bewegung des Mittelpunktes des Einheitskreises auch vor und zurŸck.

7.4      Lahme Kamera

Die folgende Abbildung zeigt die Situation fŸr , die Kamera bewegt sich halb so schnell wie der Mittelpunkt des Einheitskreises.

 

 

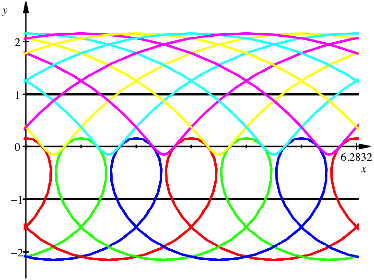
Die Kreise unten (rot, grŸn, blau) werden zu verlŠngerten Zykloiden verschmiert.

7.5      Marktbreit-Dreieck

Zum Schluss das Marktbreit-Dreieck (), aufgenommen von einer Kamera mit .

 

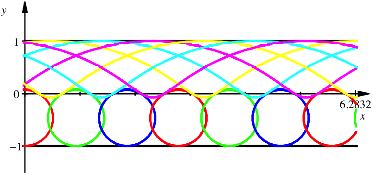
Marktbreit-Dreieck mit

 

Wir haben wie beim gewšhnlichen Reuleaux-Dreieck unten Kreise und oben verkŸrzte Zykloiden, aber die Kurven passen genau in den Zwischenraum zwischen Boden und Rollgutunterkante. Die PeriodenlŠnge ist nicht in einem rationalen VerhŠltnis zu , da p irrational ist.