Hans
Walser, [20090726a]
Regular K-gon,
Rectangles, and Trapezoids
1 WhatŐs about
We
start with a regular K-gon and add similar
rectangles on every side. The shape of the rectangles depends on K: 
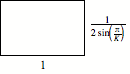
Shape
of the rectangles
Then
we proceed by adding rectangles, as explained in the next example.
The
lengths of the different rectangles are in the proportions 1:1:2:3:5:8É, i. e.
in the proportions of the Fibonacci-numbers.
2
Example
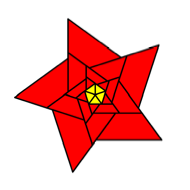
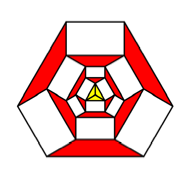
Starting
by a regular yellow pentagon (
) in the unit circle we add similar rectangles 
on every side.
Then we proceed as indicated in the following figure.
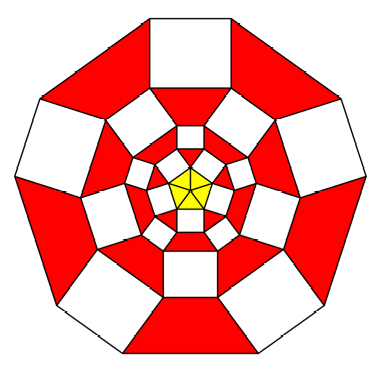
Pentagon
and rectangles
We get
red isosceles trapezoids between the white rectangles. In the first ring we see
red triangles, but we count them as special red trapezoids with upper side
zero.
Remark:
There is (of course) a link to the golden section 
, since 
.
Dissecting
the rectangles into congruent rhombuses, we see that the lengths of the rectangles
are 1, 1, 2, 3, É . These are the
Fibonacci Numbers.
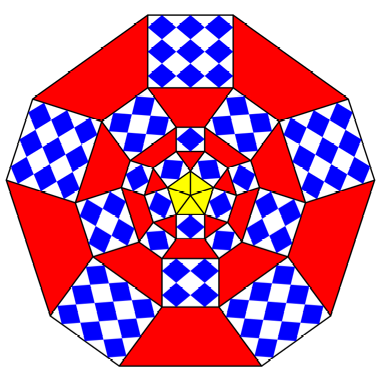
Congruent
rhombuses
We can
dissect the triangles and trapezoids into congruent triangles and hexagons
(both not regular).
Nice
figure
3
Modification
We can
modify the figure by transforming the white rectangles into parallelograms.
This does not change shape or size of the red trapezoids.
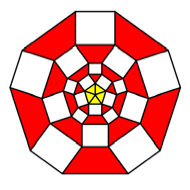
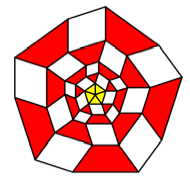
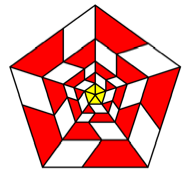
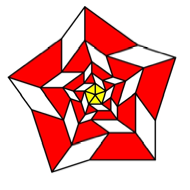
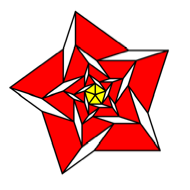
Collapsing
the rectangles
Most
useful is the third of these figures with five sectors.
All
these figures can be dissected into parallelograms (instead of rhombuses) and
triangles and hexagons. The triangles and hexagons donŐt change their shape or
size.
Modification
4
Some calculations
We use
the notations of the following figure.
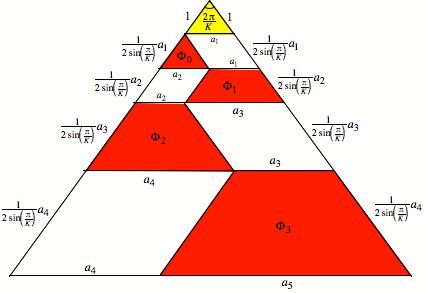
Notations
First
we get:
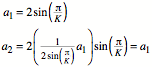
Studying
a red trapezoid, we see:
This
is the usual Fibonacci recursion. Therefore we have:
For
the areas 
of the red
trapezoids we get by some calculations:
These
are every second Fibonacci number. The areas of the red trapezoids are in a rational
relation.
5
Special cases
5.1
K = 1
Division
by zero.
5.2
K = 2
We use
rectangles with 
(half squares).
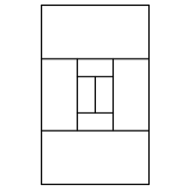
K = 2
The
entire Figure is a rectangle, which approximates the so called Golden Rectangle
with 
.
5.3
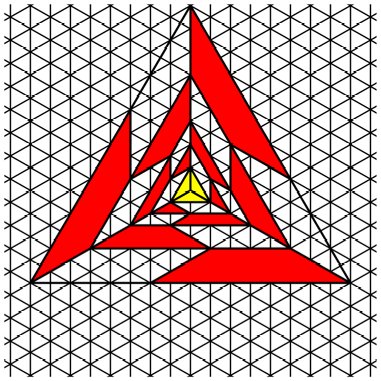
K = 3
We use
rectangles with 
.
K = 3
Both
figures fit in the same triangular lattice. In this lattice it is easy to check
the Fibonacci property.
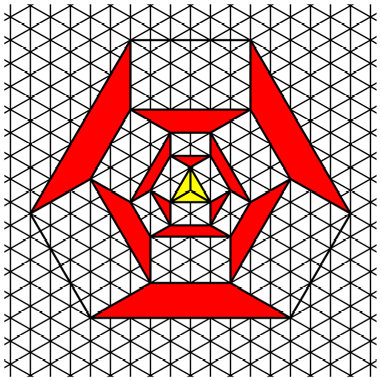
Triangular
lattice
Triangular
lattice
Dissections
5.4
K = 4
We use
rectangles with 
. This is the so
called DIN format.
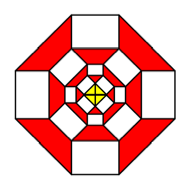
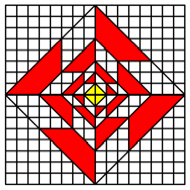
K = 4
The
figure on the right fits into a square lattice, but not so the figure on the
left.
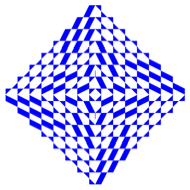
Disections
5.5
K = 5
See
example in the introduction.
5.6
K = 6
We get
ŇrectanglesÓ with 
, i. e. squares.
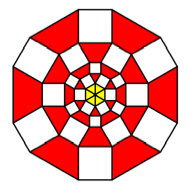
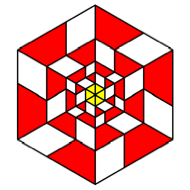
K = 6
The
figure on the right fits into a regular triangular lattice. The figure on the
left not, since rectangles and regular triangles donŐt like each other.
Triangular
lattice
In the
dissection of the figure on the left we get squares, equilateral triangles, and
regular hexagons. This is the most regular case.
Squares,
equilateral triangles, and regular hexagons
Pattern
in a hexagon
5.7
K = 7
We use
rectangles with 
. Now the rectangles are staying out like the hairs of
Struwwelpeter.
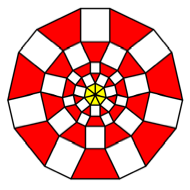
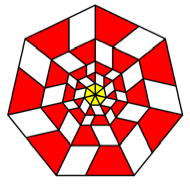
K = 7
5.8
K = 8
Rectangles
with 
.
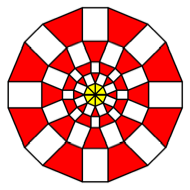
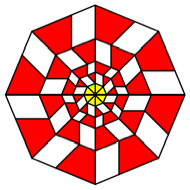
K = 8
5.9
K = 10
Rectangles
with 
. We have golden
rectangles.
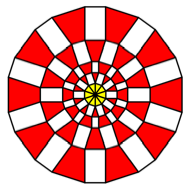
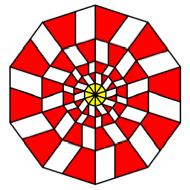
K = 10
5.10
K = 30
K = 30
The
figure approximates circles with the radii 1, 2, 3, 5, and 8, i. e. the
Fibonacci numbers.
Dissection
References
[Deshpande 2009] Deshpande, M. N. : Proof Without
Words: Beyond Extriangles. MATHEMATICS MAGAZINE. Vol. 82, No. 3, June 2009, p.
208.