Hans Walser, [20140616]

Regelmäßige Korbbögen

Anregung: H. K. S., L.

1 Worum geht es?

Auf der Basis von regelmäßigen Vielecken werden aus Kreisbögen zusammengesetzte Figuren (Korbbögen) gebildet.

Dabei sind Fallunterscheidungen bezüglich der Parität der Eckenzahl erforderlich.

2 Möglichst spitze Sterne

In einem regelmäßigen n-Eck , n ≥ 3, zeichnen wir mit Diagonalen einen „möglichst spitzen“ Stern mit nicht verschwindender Fläche (Abb. 1).

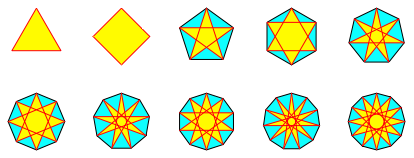
Abb. 1: Weißt du wie viel Sternlein stehen?

3 Fallunterscheidungen

Es drängen sich folgende Fallunterscheidungen auf.

3.1 Ungerade Eckenzahl

Bei ungerader Eckenzahl n = 3, 5, 7, ... ist der Stern von der Form mit (Schreibweise nach (Coxeter, 1973), S. 93).

Die geometrische Bedeutung der Notation ist folgende: Die Zahl n bedeutet die Eckenzahl des zugrundeliegenden regelmäßigen n-Ecks. Nun starten wir bei einer Ecke und zählen auf dem Umkreis j Ecken weiter. Das ist dann der nächste Eckpunkt des Sterns. Und so weiter.

Die Randlinie eines möglichst spitzen Sterns mit n = 3, 5, 7, ... kann in einem Zug aus Diagonalen gezeichnet werden. Es werden die längstmöglichen Diagonalen des n-Ecks verwendet.

3.2 Gerade Eckenzahl

Bei gerader Eckenzahl ist Stern von der Form mit . Es werden die zweitlängsten Diagonalen des n-Ecks verwendet.

Nun ist aber eine Binnen-Fallunterscheidung erforderlich.

3.2.1 Vielfache von 4 als Eckenzahl

Für n = 4, 8, 12, ... kann die Randlinie des Sterns in einem Zug aus Diagonalen gezeichnet werden.

3.2.2 Ungerade gerade Eckenzahl

Die Zahlen n = 2, 6, 10, 14, ... , also , werden manchmal als „ungerade gerade Zahlen“ bezeichnet. Sie sind das Doppelte einer ungeraden Zahl. In der Folge 2, 4, 6, 8, ... der geraden Zahlen besetzen sie die ungeraden Positionen.

Für n = 6, 10, 14, ... kann die Randlinie nicht mehr in einem Zug aus Diagonalen gezeichnet werden. Der Stern zerfällt in zwei Substerne von der Form mit und . So zerfällt etwa der Stern für n = 10 in zwei Pentagramme.

Bemerkung 1: Die Randlinie kann immer noch in einem Zug gezeichnet werden, allerdings braucht es dann Richtungsänderungen bei Binnenschnittpunkten von Diagonalen.

Bemerkung 2: Die vorliegende Fallunterscheidung spielt auch in anderen Überlegungen bei regelmäßigen n-Ecken ein Rolle, etwa der Frage, wie diese n-Ecke durch Streifen gefaltet werden können.

4 Korbbögen

Korbbögen sind Kurven, die sich aus Kreisbögen mit glatten Übergängen zusammensetzen (vgl. (Giering, 1992), (Walser, 1996), Weblink [1]). Trotz des glatten Überganges von einem Bogen zum nächsten sind Korbbögen als Verkehrstrassen aber ungeeignet da beim Übergang eine abrupte Krümmungsänderung vorliegt (Entgleisungsgefahr).

Wir ergänzen nun unsere Sterne mit geschlossenen Korbbögen. Die Spitzen der Sterne werden in geeigneter Reihenfolge als Zentren der Bögen verwendet. Die Seiten der Sterne müssen geeignet verlängert werden.

Dazu arbeiten wir mit obiger Fallunterscheidung bezüglich der Eckenzahl n.

4.1 Ungerade Eckenzahl

Die Abbildung 2 zeigt die Situation für n = 3, 5 und 7. Es entstehen Kurven konstanten Durchmessers (Orbiforme, Gleichdicks, vgl. Weblinks [2], [3], [4]).

Abb. 2: Gleichdicks

4.2 Gerade Eckenzahl

Bei geraden Eckenzahlen gibt es jeweils zwei Möglichkeiten. Die Abbildung 3 zeigt die beiden Möglichkeiten für n = 4.

Man beachte, dass es sich nicht um Ellipsen handelt. Ellipsen haben stetige Krümmungsänderungen.

Die Kurven sind offensichtlich auch keine Gleichdicks.

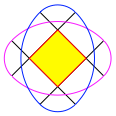
Abb. 3: Zwei Lösungen

Im Folgenden wird jeweils nur eine Kurve gezeichnet.

4.2.1 Vielfache von 4 als Eckenzahl

Die Abbildung 3 zeigt die beiden Kurve für n = 4. Die Abbildung 4 zeigt je eine Kurve für n = 8 und 12. Die ins Leere schauenden Spitzen sind Zentren der großen Bögen.

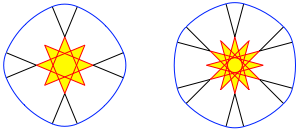
Abb. 4: Achtstern und Zwölfstern

4.2.2 Ungerade gerade Eckenzahl

Wegen des Zerfalls in zwei Sterne ungerader Eckenzahl erhalten wir Gleichdicks als Lösungen. Die ins Leere schauenden Spitzen sind belanglos. Die Abbildung 5 zeigt die Situation für n = 6.

Abb. 5: Gleichdick

5 Stumpfer Stern

Wir lassen nun die Bedingung „möglichst spitz“ für die Sterne fallen. Die Abbildung 6 zeigt einen in diesem Sinne „stumpfen“ Stern auf der Basis n = 7. In der Coxeter-Notation ist dies der Stern .

Abb. 6: Stumpfer Stern

Mit den Bögen wird es nun spannend. Wir erhalten die Figur der Abbildung 7.

Abb. 7: Dreifacher Umlauf

Es ergibt sich eine geschlossene Kurve mit dreifachem Umlauf, oder, wie man sagt, mit der Umlaufszahl 3. Die totale Richtungsänderung ist . Im Innern sind wir dreifach eingebüxt.

Da n = 7 ungerade ist, fragen wir nach einem Gleichdick. Dazu modifizieren wir den Begriff „Durchmesser“. Ein Durchmesser liegt auf einer Transversalen, welche die Kurve zweimal orthogonal schneidet. Der Durchmesser ist dann die Länge der Strecke zwischen den beiden Schnittpunkten. Man beachte, dass dieser Durchmesserbegriff kompatibel ist mit dem bisherigen Begriff eines Durchmessers etwa eines Kreises oder eines Gleichdicks der Abbildung 2. Die Abbildung 8 zeigt einen solchen Durchmesser für die Kurve der Abbildung 7. Der Durchmesser verläuft durch einen Punkt des zugrundeliegenden Siebenecks.

Abb. 8: Durchmesser

Wenn wir diesen Durchmesser nun abdrehen, bleibt seine Länge konstant. Wir haben es also mit einem Gleichdick zu tun.

Literatur

Coxeter, H.S.M. (1973): Regular Polytopes. Third Edition. New York: Dover 1973. ISBN 0-486-61480-8.

Giering, Oswald (1992): Zur Geometrie der Polygon-Korbbögen. PM, Praxis der Mathematik (34), S. 245-248.

Walser, Hans (1996): Geschlossene Korbbögen. PM, Praxis der Mathematik (38), 169-172.

Weblinks

Abgerufen 16. 6. 2014.

[1]

http://www.walser-h-m.ch/hans/Miniaturen/K/Korbboegen/Korbboegen.pdf

[2]

http://www.walser-h-m.ch/hans/Miniaturen/G/Gleichdick/Gleichdick.htm

http://www.walser-h-m.ch/hans/Miniaturen/G/Gleichdick/Gleichdick.pdf

[3]

http://www.walser-h-m.ch/hans/Miniaturen/G/Gleichdick_Kartoffeln/Gleichdick_Kartoffeln.htm

[4]

http://www.walser-h-m.ch/hans/Miniaturen/G/Gleichdick_Zykloide/Gleichdick_Zykloide.htm

http://www.walser-h-m.ch/hans/Miniaturen/G/Gleichdick_Zykloide/Gleichdick_Zykloide.pdf