Hans Walser, [20201011]

Anregung: Thomas Jahre, Aufgabe 651

RegelmŠ§ige Vielecke

1     Aufgabenstellung

(redigierte Fassung)

Zwei Seiten des gelben Einheitsquadrates werden nach rechts beziehungsweise nach oben durch Ansetzen einer Strecke der LŠnge p verlŠngert (Abbildung 1a fŸr p = 1). Dann ergŠnzen wir zu einem neuen Quadrat. Der FlŠcheninhalt des neuen Quadrats ist m mal so gro§ wie der FlŠcheninhalt des gelben Einheitsquadrates.

Berechne die natŸrliche Zahl m.

Man kann eine entsprechende Konstruktion auch mit einem anderen regelmŠ§igen n-Eck beginnen und die VerhŠltnisse der FlŠcheninhalte ermitteln. Au§er n = 4 gibt es nur zwei Werte fŸr n, so dass die passende Zahl m eine natŸrliche Zahl ist. Welche n-Ecke sind das und wie gro§ ist das passende m?

2     Quadrat

Die Abbildung 1a zeigt die Situation fŸr das Quadrat und p = 1.

Es ist m = 5 (Zerlegungsbeweis Abb. 1b und 1c).

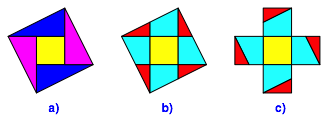
Abb. 1: VerfŸnffachung des Quadrates

Es gibt fŸr jede natŸrliche Zahl p eine Lšsung.

Es ist dann m = (p + 1)2 + p2 = 2p2 + 2p + 1. Beweis mit dem Satz des Pythagoras.

3     Gleichseitiges Dreieck

Die Abbildung 2a zeigt die Situation fŸr das gleichseitige Dreieck und p = 1.

Es ist m = 7 (Zerlegungsbeweis Abb. 2b und 2c).

 

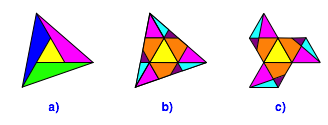
Abb. 2: Versiebenfachung des Dreieckes

Es gibt fŸr jede natŸrliche Zahl p eine Lšsung.

Es ist dann m = (p + 1)2 + p2 + p(p + 1) = 3p2 + 3p + 1. Beweis mit dem Kosinus-Satz.

4     RegelmŠ§iges Sechseck

Die Abbildung 3a zeigt die Situation fŸr das regelmŠ§ige Sechseck und p = 1.

Es ist m = 3 (Zerlegungsbeweis Abb. 3b bis 3e).

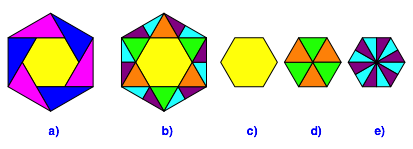
Abb. 3: Verdreifachung des Sechseckes

Es gibt fŸr jede natŸrliche Zahl p eine Lšsung.

Es ist dann m = (p + 1)2 + p2 – p(p + 1) = p2 + p + 1. Beweis mit dem Kosinus-Satz.

5     Andere Vielecke?

Wenn wir verlangen, dass p eine natŸrliche Zahl sein soll, gibt es nur die obigen Lšsungen. Das liegt daran, dass  nur fŸr n = 2, 3, 4, 6 eine rationale Zahl ist. Das ist ein nicht leicht einzusehender zahlentheoretischer Sachverhalt.

Insbesondere fŸr n = 5 ist: . Dies ist eine irrationale Zahl.

Wenn p eine reelle Zahl sein darf (aber m nach wie eine natŸrliche Zahl), gibt es fŸr jedes n-Eck beliebig viele Lšsungen.

Zum Beispiel kšnnen wir mit

 

                                                                               (1)

 

 

 

das regelmŠ§ige FŸnfeck verdoppeln (Abb. 4). Beim Zerlegungsbeweis ist zu beachten dass die kleinen Dreiecke in den Abbildungen 4b und 4d gegengleich orientiert sind.

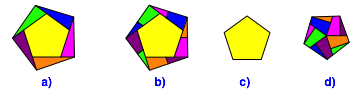
Abb. 4: Verdoppelung des FŸnfeckes

6     Allgemein

Wir kšnnen die Zahl m beliebig wŠhlen. Zu gegebenem n finden wir p als Lšsung der quadratischen Gleichung:

 

                                                               (2)

 

 

 

Beweis mit dem Kosinus-Satz.