Hans Walser, [20160502]
Quadratzahlenfolge
1 Worum geht es?
Es werden rekursiv definierte Folgen vorgestellt, die ausschlie§lich aus Quadratzahlen bestehen.
2 Beispiel
Die durch die Rekursion
(1)
mit den Startwerten
(2)
definierte Folge besteht ausschlie§lich aus Quadratzahlen.
FŸr den geometrischen Hintergrund siehe [1].
3 Symmetrie
ZunŠchst eine Bemerkung zur Symmetrie. Die eilige Leserin kann diese Bemerkung Ÿberspringen.
Wenn wir die Folge rŸckwŠrts laufen lassen, erhalten wir aus (1) die Rekursion.
(3)
Da auch die Startwerte bezŸglich der Null symmetrisch sind haben wir eine symmetrische Folge:
(4)
4 Bearbeitung
4.1 Tabelle
Die Tabelle 1 gibt die ersten Werte mit nichtnegativem Index.
|
n |
an |
|
|
0 |
0 |
0 |
|
1 |
1 |
1 |
|
2 |
4 |
2 |
|
3 |
25 |
5 |
|
4 |
144 |
12 |
|
5 |
841 |
29 |
|
6 |
4900 |
70 |
|
7 |
28561 |
169 |
|
8 |
166464 |
408 |
|
9 |
970225 |
985 |
|
10 |
5654884 |
2378 |
Tab. 1: Werte und Wurzeln
4.2 Explizite Formel
Die explizite Formel fŸr die Folge an finden wir wie folgt.
Aus der Rekursion (1) bauen wir die kubische Gleichung:
(5)
Diese hat die drei Lšsungen:
(6)
Bemerkung fŸr Lehrer: die Lšsung x3 = –1 ãsiehtÒ man sofort.
FŸr die explizite Formel machen wir den Ansatz:
(7)
Einsetzen der drei Startwerte (2) liefert ein lineares Gleichungssystem fŸr {p, q, r} mit den Lšsungen:
(8)
Die explizite Formel lautet also:
(9)
Diese Formel mŸssen wir noch mit (1) und (2) induktiv verifizieren (mit CAS).
4.3 Heuristisches Vorgehen
Aus der Tabelle 1 ersehen wir die Quadratwurzeln fŸr die ersten 11 Werte. Wir vermuten, dass dazu die Rekursion
(10)
passt. Jedenfalls kšnnen wir fŸr die Folge bn mit der Rekursion (10) und den Startwerten (aus der Tabelle 1)
(11)
die explizite Formel bestimmen. Dies geht analog zum obigen Beispiel. Aus (10) bauen wir die quadratische Gleichung:
(12)
Mit den beiden Lšsungen
(13)
machen wir den Ansatz:
(14)
Wir setzen die Startwerte (11) ein und erhalten ein lineares Gleichungssystem fŸr {p, q} mit den Lšsungen:
(15)
Damit haben wir die explizite Formel
(16)
welche mit (10) und (11) induktiv verifiziert wird.
4.4 Beweis der Quadrateigenschaft
Und nun kommt der Gag. Es ist
(17)
Damit ist bewiesen, dass (1) und (2) eine Folge generieren, die ausschlie§lich aus Quadratzahlen besteht.
Der ProblemschlŸssel ist die Beziehung:
(18)
5 †bungsaufgabe
Die durch die Rekursion
(19)
mit den Startwerten
(20)
definierte Folge besteht ausschlie§lich aus Quadratzahlen.
6 Allgemein
6.1 Die Folge
Die Folge mit den Startwerten (2) und der Rekursion
(21)
besteht ausschlie§lich aus Quadratzahlen. Und zwar sind es die Quadrate der Folgenglieder bn mit den Startwerten (11) und der Rekursion:
(22)
Der Beweis lŠuft analog zum obigen speziellen Beispiel (das Beispiel steht fŸr k = 2).
6.2 Explizite Formel
Wir bilden aus der Rekursion (21) die kubische Gleichung:
(23)
Diese hat die Lšsungen:
(24)
FŸr die explizite Formel machen wir den Ansatz:
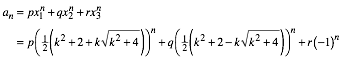(25)
Einsetzen der drei Startwerte (2) liefert ein lineares Gleichungssystem fŸr {p, q, r} mit den Lšsungen:
(29)
Die explizite Formel lautet also:
(30)
Diese Formel mŸssen wir noch mit (2) und (21) induktiv verifizieren.
6.3 Heuristisches Vorgehen
Wir bilden die Folge bn mit den Startwerten (10) und der Rekursion:
(31)
FŸr diese Folge bn bestimmen wir die explizite Formel. Aus (31) bauen wir die quadratische Gleichung:
(32)
Mit den beiden Lšsungen
(33)
machen wir den Ansatz:
(34)
Wir setzen die Startwerte (11) ein und erhalten ein lineares Gleichungssystem fŸr {p, q} mit den Lšsungen:
(35)
Damit haben wir die explizite Formel
(36)
welche mit (11) und (32) induktiv verifiziert wird.
6.4 Beweis der Quadrateigenschaft
Und nun kommt der Gag. Es ist
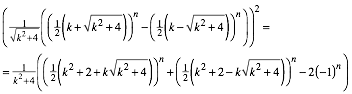(37)
Damit ist bewiesen, dass (2) und (21) eine Folge generieren, die ausschlie§lich aus Quadratzahlen besteht.
Der ProblemschlŸssel ist die Beziehung:
(38)
6.5 Beispiele
FŸr k = 0 erhalten wir:
|
n |
an |
bn |
|
0 |
0 |
0 |
|
1 |
1 |
1 |
|
2 |
0 |
0 |
|
3 |
1 |
1 |
|
4 |
0 |
0 |
|
5 |
1 |
1 |
|
6 |
0 |
0 |
|
7 |
1 |
1 |
|
8 |
0 |
0 |
|
9 |
1 |
1 |
|
10 |
0 |
0 |
Tab. 2: k = 0
Das Beispiel ist nicht eben umwerfend.
FŸr k = 1 ergeben sich die Quadrate der Fibonacci-Zahlen (Tab. 3). Einmal mehr sind die Fibonacci-Zahlen das einfachste nichttriviale Beispiel.
Das war auch die †bungsaufgabe.
|
n |
an |
bn |
|
0 |
0 |
0 |
|
1 |
1 |
1 |
|
2 |
1 |
1 |
|
3 |
4 |
2 |
|
4 |
9 |
3 |
|
5 |
25 |
5 |
|
6 |
64 |
8 |
|
7 |
169 |
13 |
|
8 |
441 |
21 |
|
9 |
1156 |
34 |
|
10 |
3025 |
55 |
Tab. 3: Quadrate der Fibonacci-Zahlen
Die Tabelle 1 zeigt die Zahlen fŸr k = 2.
Und noch die Tabelle 4 fŸr k = 3.
|
n |
an |
bn |
|
0 |
0 |
0 |
|
1 |
1 |
1 |
|
2 |
9 |
3 |
|
3 |
100 |
10 |
|
4 |
1089 |
33 |
|
5 |
11881 |
109 |
|
6 |
129600 |
360 |
|
7 |
1413721 |
1189 |
|
8 |
15421329 |
3927 |
|
9 |
168220900 |
12970 |
|
10 |
1835008569 |
42837 |
Tab. 4: k = 3
6.6 Zahlendreiecke
Im Folgenden (39) die ersten 11 Folgenglieder an in allgemeiner Form.
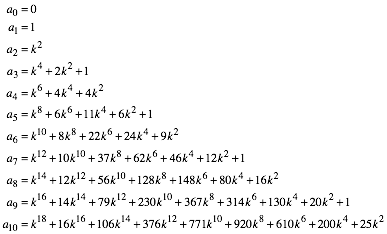(39)
Es entsteht ein Koeffizientendreieck, das sich mir nicht erschlie§t.
In (40) die ersten 11 Folgenglieder von bn.
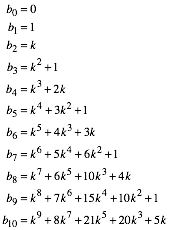(40)
Das Koeffizientendreieck ist ein affin verzerrtes Pascal-Dreieck (Binomialkoeffizienten). Die Spalten sind je mit einem zusŠtzlichen Versatz nach unten verschoben. Die Zeilensummen der Koeffizienten sind nun die Fibonacci-Zahlen.
Wir haben entweder nur gerade oder nur ungerade Exponenten.
Weblink
[1] (2. 5. 2016)
http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadrate_ansetzen2/Quadrate_ansetzen2.htm
http://www.walser-h-m.ch/hans/Miniaturen/Q/Quadrate_ansetzen2/Quadrate_ansetzen2.pdf