Hans Walser, [20160631]
Quadratsummen-Spirale
Anregung: Heinz Klaus Strick, Leverkusen
1 Worum geht es?
Wir zeichnen mit rechtwinkligen Dreiecken eine eckige Spirale gem§ Abbildung 1. Die roten Katheten haben der Reihe nach die Lngen 1, 2, 3, 4, 5, 6, 7, ... .
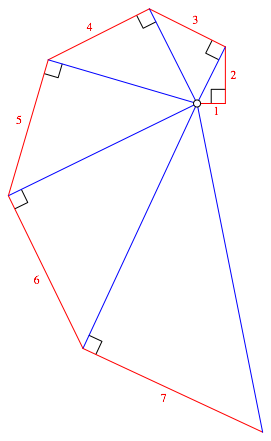
Abb. 1: Die ersten sieben Schritte
Die Abbildung 2 zeigt die ersten 200 Schritte. Was fr eine Spirale ist das?
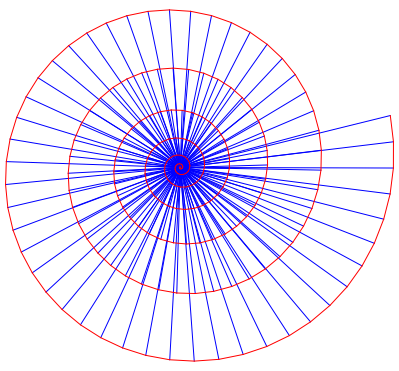
Abb. 2: Spirale
Eine archimedische Spirale kann es nicht sein, da die Abstnde zwischen den Spiralendurchgngen wachsen.
Fr eine logarithmische Spirale wachsen aber diese Abstnde zu wenig rasch.
2 Speichenlngen
Wir berechnen die blauen Speichenlngen rn (Abb. 3, Tab. 1)
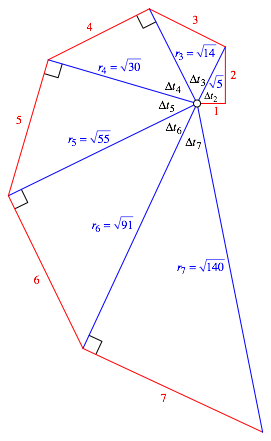
Abb. 3: Speichenlngen
|
n |
rn |
Radikand |
|
1 |
|
1 =
12 |
|
2 |
|
5 =
12 + 22 |
|
3 |
|
14 = 12 + 22 + 32 |
|
4 |
|
30
= 12 + 22 + 32 + 42 |
Tab. 1: Speichenlngen
Es ist:
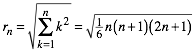 (1)
(1)
Daher der Name ãQuadratsummen-SpiraleÒ.
3 Typ der Spirale
Mit ![]() bezeichnen
wir den spitzen Winkel der rechtwinkligen Dreiecke im Zentrum (Abb. 3). Es ist:
bezeichnen
wir den spitzen Winkel der rechtwinkligen Dreiecke im Zentrum (Abb. 3). Es ist:
![]() (2)
(2)
Nun berlegen wir, was ãjanz weit au§enÒ, also fr gro§e n geschieht. Zunchst ist:
![]() (3)
(3)
Weiter ist:
![]() (4)
(4)
Wir betrachten nun n als reelle Variable und berechnen den Polarwinkel t in Abhngigkeit von n.
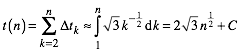 (5)
(5)
Somit ist:
![]() (6)
(6)
Dies setzen wir in (3) ein:
![]() (7)
(7)
Unsere Spirale ist also im Wesentlichen vom Typ:
![]() (8)
(8)
Es handelt sich um eine kubische Spirale.
Leider lsst sich die kubische Spirale nicht so leicht manipulieren wie die logarithmische Spirale. Insbesondere hat die kubische Spirale keine Drehstrecksymmetrie.
In den beiden folgenden Abbildungen sind die Parameter a und b jeweils so gewhlt worden, dass die kubische Spirale (magenta) durch die beiden letzten Eckpunkte der roten eckigen Spirale verluft. Fr die brigen Eckpunkte der roten Spirale gilt die kubische Spirale nur nherungsweise.
In der Abbildung 4 sind die ersten sieben Schritte gezeichnet.
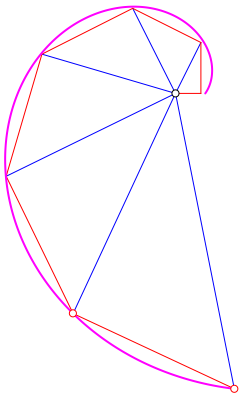
Abb. 4: Die ersten sieben Schritte
Die Abbildung 5 zeigt die ersten 200 Schritte mit der kubischen Spirale. Die Approximation ist so gut, dass die ursprngliche eckige Spirale zugedeckt wird.
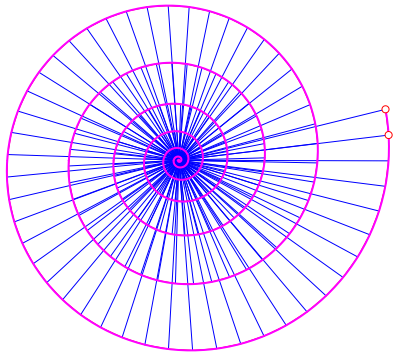
Abb. 5: Spiralen