1 n = 3

Die Liste zeigt die 6 Permutationen. Grün die geraden, rot die ungeraden Permutationen.

123 132 213 231 312 321

Permutationen

Diese lassen sich im Dreieck illustrieren. Wir nummerieren die Dreiecksecken:

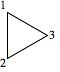
Nummerierte Dreiecksecken

Dann zeichnen wir für jede Permutation einen Vektorzug:

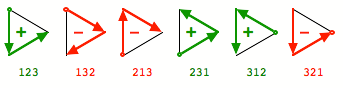
Vektorzüge

Bei den geraden Permutationen (grün) haben die beiden aufeinander folgenden Vektoren einen Zwischenwinkel von , es geht im positiven Drehsinn herum; bei den ungeraden Permutationen (rot) haben die beiden aufeinander folgenden Vektoren einen Zwischenwinkel von und es geht im negativen Drehsinn herum.

Alle grünen Vektorzüge lassen sich durch eine Drehung aufeinander abbilden, sie sind also gleich orientiert. Zwischen einen grünen und einem roten Vektorzug braucht es zusätzlich eine Geradenspiegelung.

2 n = 4

Die Liste zeigt die 24 Permutationen.

1234 1243 1324 1342 1423 1432

2134 2143 2314 2341 2413 2431

3124 3142 3214 3241 3412 3421

4123 4132 4213 4231 4312 4321

Permutationen

Zur Illustration arbeiten wir im Raum mit einem eckennummerierten Tetraeder.

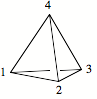
Tetraeder

Dann zeichnen wir für jede Permutation einen Vektorzug:

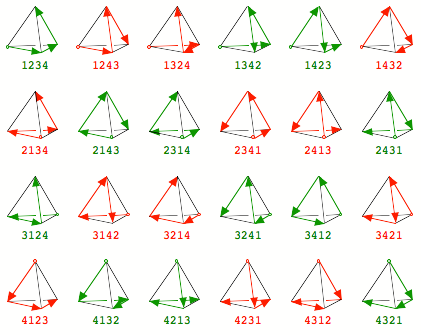
Vektorzüge

Bei den geraden Permutationen (grün) verhält sich der jeweilige Vektorzug wie eine Rechtsschraube, bei den ungeraden Permutationen wie eine Linksschraube. Wir müssen also nicht mehr die Krümmung, sondern die Torsion beachten.

Man kann es auch so sehen: Alle grünen Vektorzüge lassen sich durch eine Bewegung aufeinander abbilden, sie sind also räumlich gleich orientiert. Wenn wir die drei Vektoren von einem Punkt aus starten, bilden sie in der gegebenen Reihenfolge ein Rechtssystem. Zwischen einem grünen und einem roten Vektorzug braucht es zusätzlich eine Ebenenspiegelung, welche die Raumorientierung ändert.