Hans Walser, [20100714a], [20131218a]

Parallelenkonstruktion mit Mittelpunkt

1        Worum geht es?

Es geht um die Parallelenkonstruktion unter folgenden Restriktionen.

1.1      Formulierung nach alter VŠter Sitte

Gefordert sein soll:

          I.     Dass Punkte gezeichnet werden kšnnen.

        II.     Dass zu zwei Punkten die Gerade gezeichnet werden kann.

      III.     Dass auf einer Geraden Punkte gezeichnet werden kšnnen.

      IV.     Dass zu zwei nicht parallelen Geraden deren Schnittpunkt gezeichnet werden kann.

        V.     Dass zu zwei Punkten deren Mittelpunkt gezeichnet werden kann.

1.2      Formulierung DGS

In einem DGS sind fast alle Tasten kaputt, au§er:

 Punkt

 Punkt auf Objekt

 Schnittpunkt(e)

 Gerade

 Mittelpunkt

1.3      Formulierung mit Tools

Wir dźrfen das Lineal (ohne Markierung), einen Zeichenstift und die Halbierungsschere gebrauchen. Zirkel verboten.

Die Halbierungsschere ist ein gelenkiges GerŠt. Es besteht aus sechs Teilen (in der Abbildung grźn), davon vier Teile mit zwei Gelenklšchern und zwei Teile mit drei Gelenklšchern. Abstand von Loch zu Loch źberall gleich. Lšcher werden gelenkig verbunden, in der Abbildung rot.

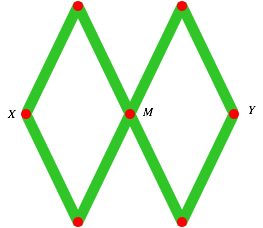
Halbierungsschere

Wir setzen nun X an den Anfang und Y an das Ende einer Strecke. Dann ist M deren Mittelpunkt. Modell nachbauen und ausprobieren.

Die Halbierungsschere kann allerdings auch als Verdoppelungsschere verwendet werden.

2        Aufgabe

Gegeben sind eine Gerade g und ein Punkt P. Zeichne die Parallele zur Geraden g durch den Punkt P.

 

 

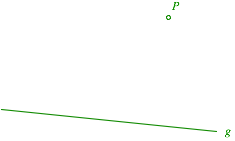
Gesucht ist die Parallele zu g durch P

3        Konstruktion

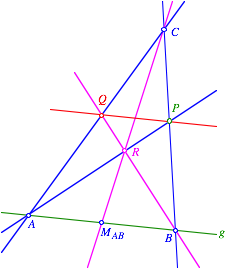
Konstruktion

Vorgehen:

1.     Auf g zwei Punkte A und B wŠhlen.

2.     Mittelpunkt  der Strecke AB.

3.     Punkt C beliebig auf der Geraden BP, aber .

4.     Zum Dreieck ABC ergŠnzen.

5.     Schwerlinie  .

6.     Schnittpunkt R der Schwerlinie mit der Geraden AP.

7.     Schnittpunkt Q der Geraden BR mit der Geraden AC.

8.     Die Gerade PQ ist die gesuchte Parallele.

4        Beweise

4.1      Kurzer Beweis

SchrŠgspieglung.

4.2      Beweis mit Ceva und StrahlensŠtzen

Wir fźhren Abschnittsbezeichnungen ein gemŠ§ Abbildung.

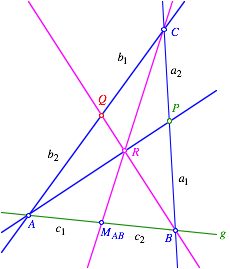
Bezeichnungen

Nach dem Satz von Ceva ist:

 

 

Wegen  folgt daraus:

 

 

Auf Grund der StrahlensŠtze folgt: Die Geraden AB und PQ sind parallel.

5        Hyperbolische Geometrie

Die Konstruktion lŠsst sich auch in der hyperbolischen Geometrie durchfźhren.

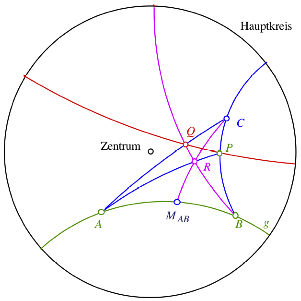
In der hyperbolischen Geometrie

Das Experiment zeigt, dass es bei verschiedenen Dispositionen von A, B und P immer eine Parallele gibt. Bei Variation von C auf der hyperbolischen Geraden BP bleibt die Parallele fest. Wenn wir aber zum Beispiel A auf g variieren, dreht die Parallele um P. Wenn A die ganze hyperbolische Gerade g durchlŠuft, ergeben sich alle zu g parallelen hyperbolischen Geraden durch P, einschlie§lich der Grenzparallelen.

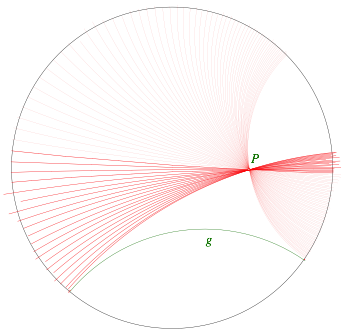
Parallelen zu g durch P

6        Verdoppelungsschere

Bei Zulassung der Verdoppelungsschere haben wir auch noch die Option Punktspiegelung. Damit ergibt sich eine sehr einfache Konstruktion.

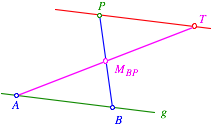
Mit Punktspiegelung

Vorgehen:

1.     Auf g zwei Punkte A und  B wŠhlen.

2.     Mittelpunkt  der Strecke BP.

3.     Den Punkt A an  spiegeln, gibt T.

4.     Die Punkte A, B, T, P bilden ein Parallelogramm.