Hans Walser, [20220523]
Ortsbogen
1 Worum geht es?
Ein Schnittpunkt und ein Schließungssatz im Umfeld des Ortsbogens.
2 Ausgangslage
Wir beginnen mit einem beliebigen Dreieck ABC und wählen drei Winkel λ, μ und ν mit der Randbedingung λ + μ + ν = 180°.
Über den Seiten a, b und c des Dreieckes ABC zeichnen wir die Ortsbogen zu den Winkeln λ, μ und ν (Abb. 1 mit λ = 45°, μ = 70° und ν = 65°).
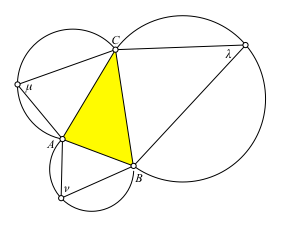
Abb. 1: Startfigur
3 Ein Schnittpunkt
Wir ergänzen die Ortsbogen zu Kreisen. Die drei Kreise kλ, kμ und kν haben einen gemeinsamen Schnittpunkt Z (Abb. 2).
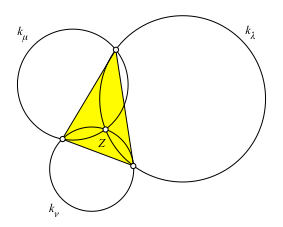
Abb. 2: Schnittpunkt
Dies kann wie folgt eingesehen werden. Wir schneiden vorerst zwei der drei Kreise (Abb. 3).
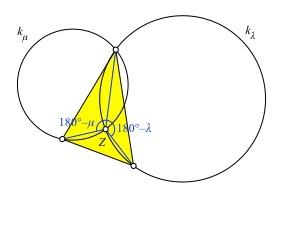
Abb. 3: Beweisfigur
Im Schnittpunkt ergeben sich die Ergänzungswinkel auf die außenliegenden Peripheriewinkel. Wegen der Randbedingung λ + μ + ν = 180° ist der fehlende Winkel der Ergänzungswinkel des dritten außenliegenden Peripheriewinkels. Daher verläuft auch der dritte Ergänzungsbogen durch den Schnittpunkt. Dies war einzusehen.
4 Eine Schließungseigenschaft
Wir wählen auf dem Kreis kλ einen beliebigen Startpunkt D und schneiden die Gerade DC mit dem Kreis kμ. Schnittpunkt E (Abb. 4).
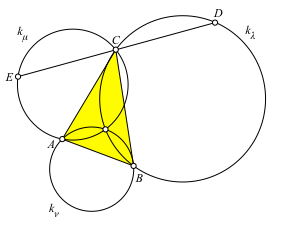
Abb. 4: Start
Nun schneiden wir die Gerade EA mit dem Kreis kν. Schnittpunkt F (Abb. 5).
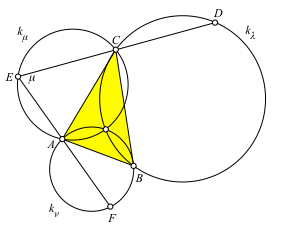
Abb. 5: Nächster Schritt
Die Gerade FB verläuft nun wieder durch D. Wir haben eine Schließungsfigur (Abb. 6).
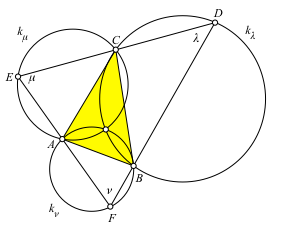
Abb. 6: Schließungsfigur
5 Ähnliche Dreiecke
Nun bewegen wir den Punkt D auf dem Kreis kλ. Damit werden auch die Punkte E und F und somit das Dreieck DEF bewegt (Abb. 7). Wegen der Invarianz der Winkel des Dreiecks DEF sind die bewegten Dreiecke alle ähnlich, und zwar gleichsinnig ähnlich.
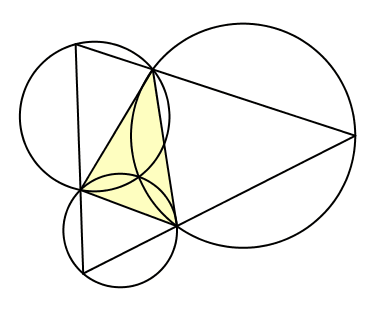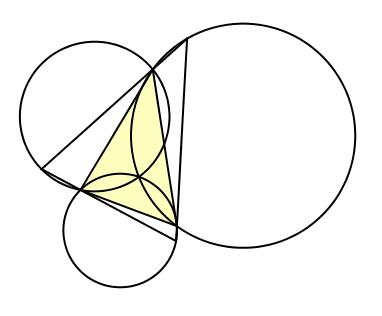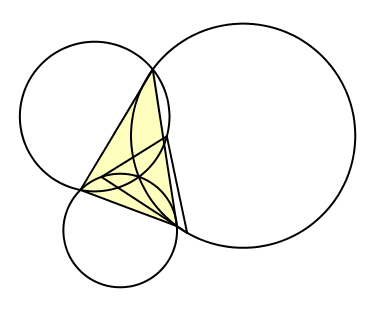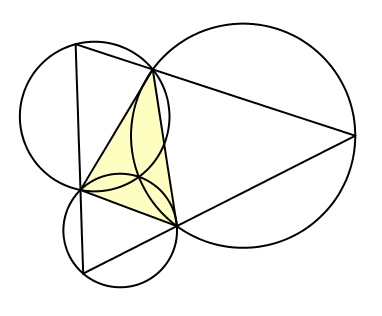
Abb. 7: Ähnliche Dreiecke
Gleichsinnig ähnliche Dreiecke können durch eine Drehstreckung aufeinander abgebildet werden. Der Abbildung 7 entnehmen wir die Vermutung, dass das Zentrum dieser Drehstreckung der Schnittpunkt Z der drei Kreise kλ, kμ und kν ist.
Für den Nachweis der Vermutung arbeiten wir mit dem blauen Teildreieck ZDE (Abb. 8). Da die Punkte Z und C festbleiben, sind der Kreis kλ auch Ortsbogen für den Winkel CDZ und der Kreis kμ Ortsbogen für den Winkel ZEC. Das blaue Dreieck ist also bei einer Bewegung von D auf dem Kreis kλ forminvariant. Da der Eckpunkt Z festbleibt, ist er das Zentrum der zugehörigen Drehstreckung.
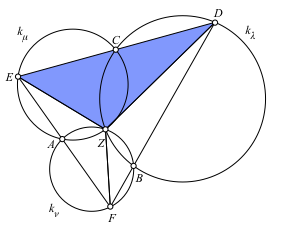
Abb. 8: Teildreieck
Die entsprechenden Überlegungen gelten auch für das rote und das grüne Teildreieck (Abb. 9).
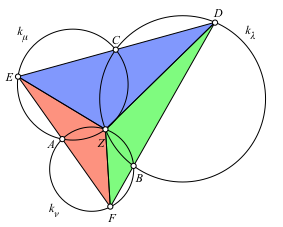
Abb. 9: Teildreiecke
Somit ist Z das Zentrum der Drehstreckungen für das Gesamtdreieck DEF (Abb. 10).
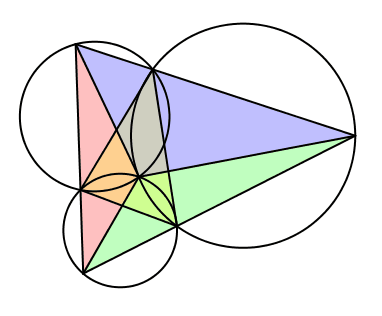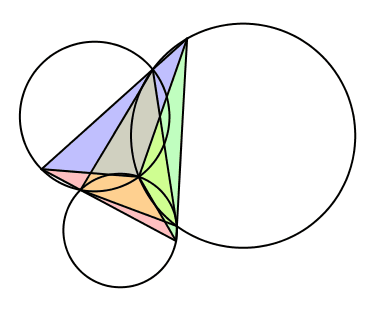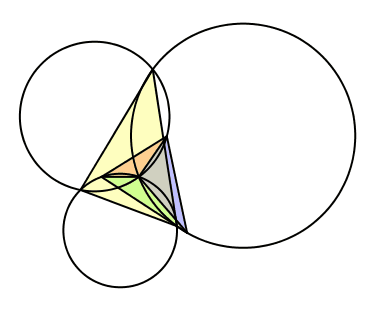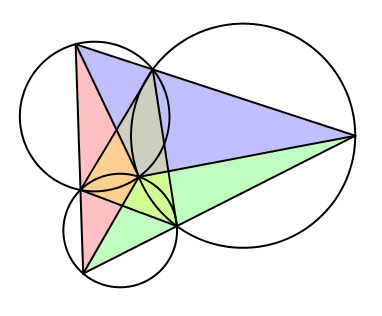
Abb. 10: Drehstreckungen
6 Sonderfälle
Die drei Winkel λ, μ und ν sind bis auf die Randbedingung λ + μ + ν = 180° beliebig wählbar. Wir wählen nun spezielle Winkel dafür. Das Dreieck ABC lassen wir unverändert.
6.1 Regelmäßiger Fall. Fermat Punkt
Wir wählen die drei Winkel gleich groß, also λ = μ = ν = 60°. Das Dreieck DEF ist gleichseitig (Abb. 11). Das Zentrum Z der Drehstreckungen ist der Fermat-Punkt des Startdreieckes ABC.
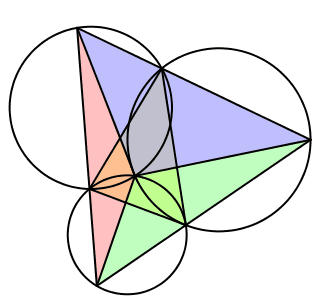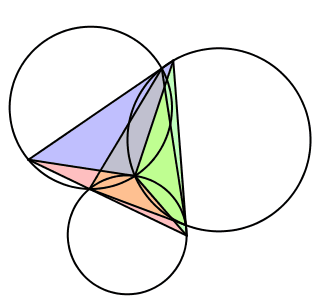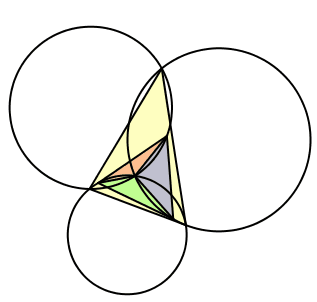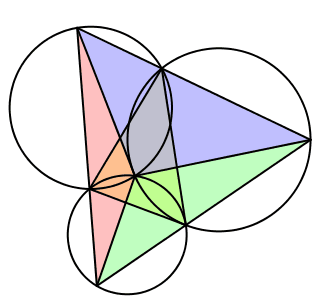
Abb. 11: Regelmäßiger Fall
6.2 Dreieckswinkel
Es seien α , β und γ die drei Winkel des Startdreieckes ABC in der üblichen Zuordnung.
E gibt 3! = 6 Möglichkeiten, diese Winkel den drei Winkeln λ, μ und ν zuzuordnen (Tab. 1).
|
|
λ |
μ |
ν |
|
1 |
α |
β |
γ |
|
2 |
γ |
α |
β |
|
3 |
β |
γ |
α |
|
4 |
α |
γ |
β |
|
5 |
β |
α |
γ |
|
6 |
γ |
β |
α |
Tab. 1: Zuordnung der Winkel
6.2.1 Fall 1
Wir setzen λ = α, μ = β und ν = γ (Abb. 12). Die drei Kreise sind alle gleich groß, nämlich so groß wie der Umkreis des Startdreieckes. Das Zentrum der Drehstreckungen ist der Höhenschnittpunkt des Startdreieckes und der Umkreismittelpunkt der bewegten ähnlichen Kreise. Das Startdreieck und die bewegten Dreiecke sind gleichsinnig ähnlich. In einer bestimmten Position ist das Startdreieck das Kantenmittendreieck des bewegten Dreiecks.
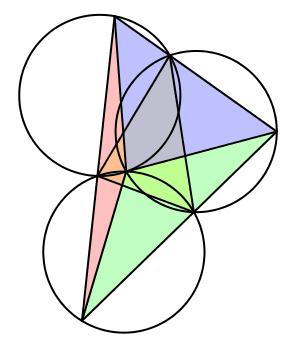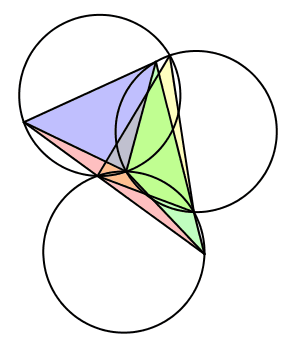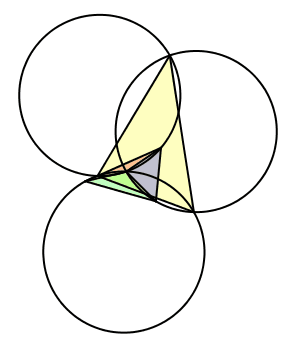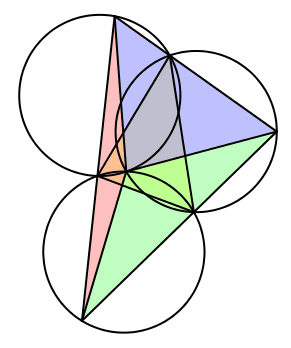
Abb. 12: Fall 1
6.2.2 Fall 2
Wir setzen λ = γ, μ = α und ν = β (Abb. 13). Gegenüber dem ersten Fall sind die Winkel zyklisch vertauscht. Die bewegten Dreiecke sind gleichsinnig ähnlich zum Startdreieck, in einer bestimmten Position sogar kongruent.
Das Besondere: Die drei Kreise sind je tangential an eine Seite des Startdreieckes. Dies folgt aus der in der Schule vermittelten Methode zur Konstruktion des Ortsbogens. Der Autor gibt zu Protokoll, dass es dieser Fall war, der ihn bewogen hat, vorliegende Studie zu schreiben.
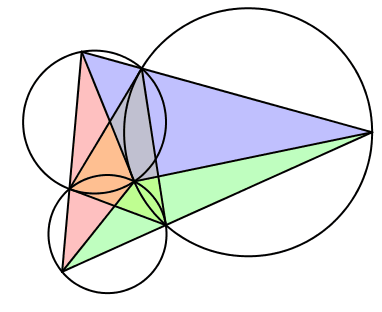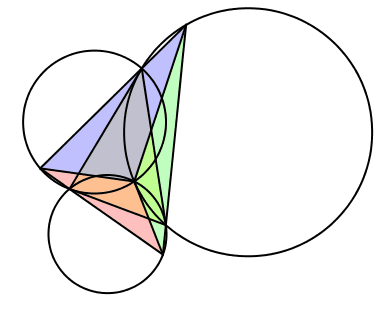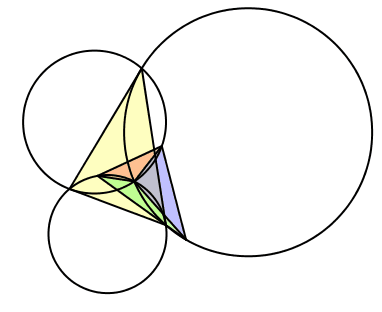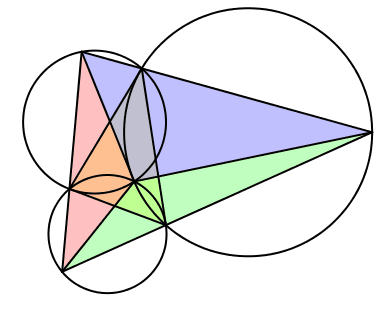
Abb. 13: Fall 2
6.2.3 Fall 3
Wir setzen λ = β, μ = γ und ν = α (Abb. 14). Gegenüber dem zweiten Fall sind die Winkel nochmals zyklisch vertauscht. Die bewegten Dreiecke sind gleichsinnig ähnlich zum Startdreieck, in einer bestimmten Position sogar kongruent.
Und wieder: Die drei Kreise sind je tangential an eine Seite des Startdreieckes. Der Fall 3 ist strukturell spiegelbildlich zum Fall 2.
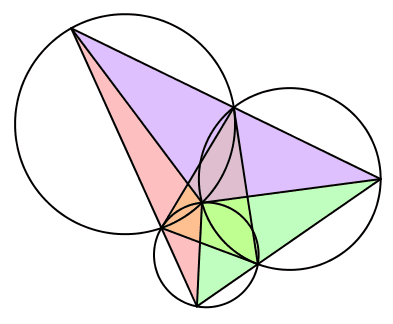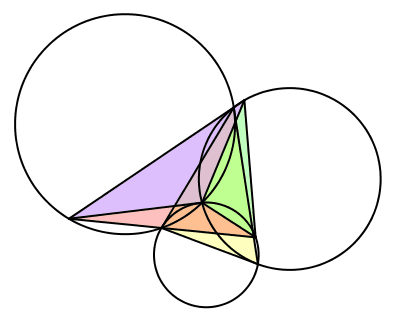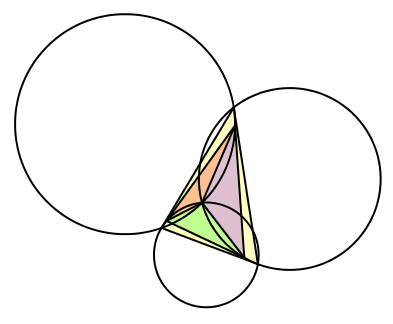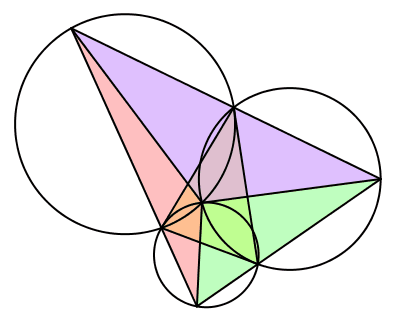
Abb. 14: Fall 3
6.2.4 Fall 4
Wir setzen λ = α, μ = γ und ν = β (Abb. 15). Wir haben eine ungerade Permutation der Winkel. Die bewegten Dreiecke sind ungleichsinnig ähnlich zum Startdreieck. Die Seite BC des Startdreieckes ist tangential zu zweien der drei Kreise. Der dritte Kreis ist gleich groß wie der Umkreis des Startdreieckes.
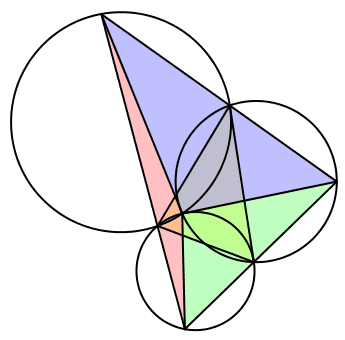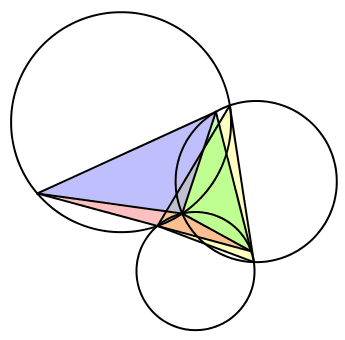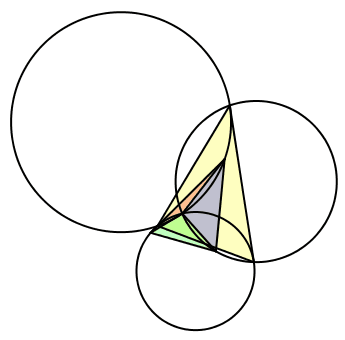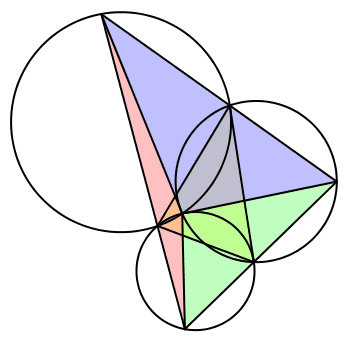
Abb. 15: Fall 4
6.2.5 Fall 5
Wir setzen λ = β, μ = α und ν = γ (Abb. 16). Die Seite AB des Startdreieckes ist tangential zu zweien der drei Kreise. Der dritte Kreis ist gleich groß wie der Umkreis des Startdreieckes.
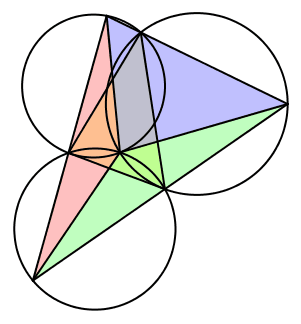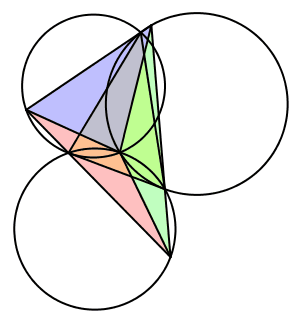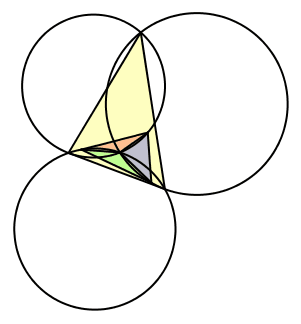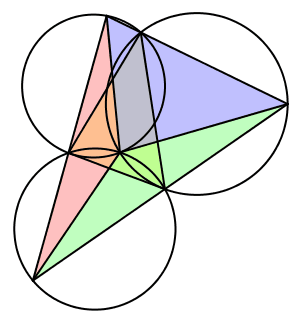
Abb. 16: Fall 5
6.2.6 Fall 6
Wir setzen λ = γ, μ = β und ν = α (Abb. 17). Die Seite CA des Startdreieckes ist tangential zu zweien der drei Kreise. Der dritte Kreis ist gleich groß wie der Umkreis des Startdreieckes.
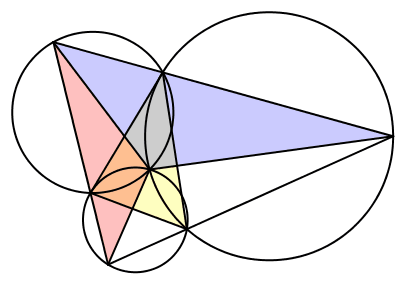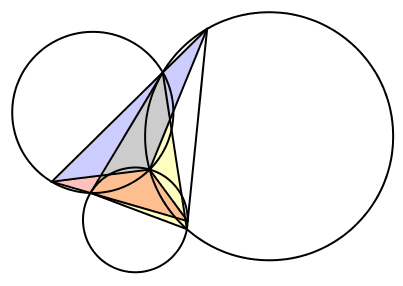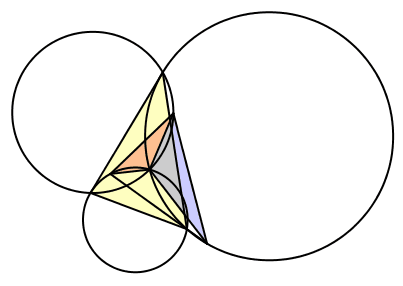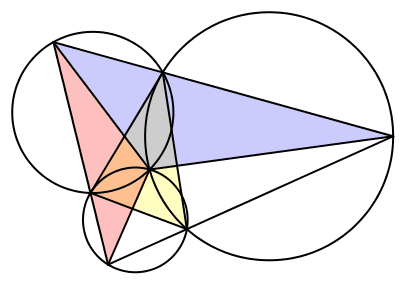
Abb. 17: Fall 6