Hans Walser, [20180416]

Origami im Raum

1 Worum geht es?

Die einfachste Faltoperation im 2d-Origami wird auf 3d-Origami übertragen.

2 In der Ebene

Wir falten zwei diametrale Ecken aufeinander (Abb. 1).

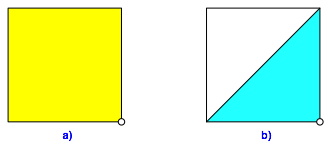
Abb. 1: Origami in der Ebene

In der Abbildung 1b ist das Papier zweilagig. Wir halben also doppelte „Dichte“

3 Im Raum

Wir ersetzen das quadratische Origami-Papier durch einen Origami-Würfel (Abb. 2a). Und wieder falten wir zwei diametrale Ecken aufeinander (Abb. 2b).

Abb. 2: Origami im Raum

Die Geometrie dahinter ist folgende: Wir halbieren den Würfel mit der Mittelnormalebene der durch die beiden diametralen Punkte definierten Raumdiagonale und spiegeln die eine Hälfte an dieser Mittelnormalebene. Vgl. (Walser 2014)

Im Innern der Figur der Abbildung 2b haben wir eine Sechskant-Pyramide doppelter Dichte.

4 Ein Papiermodell

Wir bauen ein Modell für den Körper der Abbildung 2b. Dazu verwenden wir zwei quadratische Papiere (Origami-Papiere für die Ebene, Qualität 80g/m²).

Die Abbildung 3 zeigt die Falt- und Schnittmuster.

Farbcode: grün = Schnittlinie, rot = Talfalt, blau = Bergfalt

Bei den dick gezeichneten Schnittlinien ist eher eine Nut (ca. 1mm breit) zu schneiden.

Sämtliche Schnitt- und Faltlinien sind durch einen 12×12-Quadratraster exakt definiert (dünne hellblaue Linien).

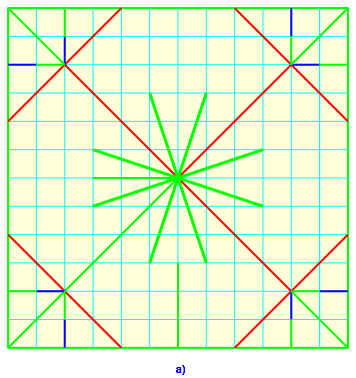
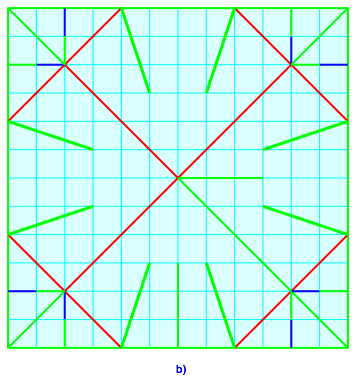
Abb. 3: Falt- und Schnittmuster der beiden Bauteile

Die beiden Bauteile sind spiegelbildlich (die Spiegelbildlichkeit ist nicht essentiell) und komplementär (was die dicken Schnittlinien betrifft).

5 Zusammenbau

Vor dem Zusammenbau empfiehlt es sich, das Modell von Walser (2013) zu bauen. Völlig analog bauen wir zunächst unsere beiden Bauteile zum aus zwei großen Würfelecken bestehenden Stern.

Dann müssen wir noch die sechs Sternspitzen zu kleinen Würfelecken umbauen. Dies geschieht im Prinzip nach derselben Technik wie bei den großen Würfelecken.

Die Abbildung 4 zeigt eine Ansicht.

Abb. 4: Ansicht

Die Abbildung 5 zeigt die Sicht von unten. Wir sehen eine Sechskant-Pyramide. Im 3d-Origami-Modell ist das die Pyramide doppelter Dichte.

Abb. 5: Sicht von unten

Diese Pyramide ist eine Hälfte der Doppelpyramide in (Walser 2018). Das Volumen dieser Pyramide ist des Würfelvolumens.

Das Volumen einer der in der Abbildung 4 sichtbaren Nasen ist des Würfelvolumens.

In der Abbildung 6 sind zwei Exemplare des Modells farbkomplementär an den Sechseckbasen der Pyramide aneinandergesetzt.

Abb. 6: Zwei Modelle

Wir erkennen den ursprünglichen gelben Würfel und ein dazu um eine Raumdiagonale um 60° verdrehter Würfel.

Diese Verdrehung kann mit der Matrix M

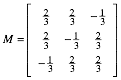(1)

beschrieben werden. Die Abbildung 7 zeigt die Situation. Wir erkennen rechts unten die Figur der Abbildung 2b.

Abb. 7: Würfel und verdrehter Würfel

Diese Würfelkonfiguration kann als Steckmodell hergestellt werden. Wir brauchen dazu 12 Quadrate (6 gelbe und 6 blaue) aus starkem Papier mit Nuten. Die Abbildung 8 zeigt das Schnittmuster eines dieser Quadrate. Die 4×4-Quadratrasterung dient der exakten Festlegung der Nuten.

Abb. 8: Schnittmuster für das Steckmodell

Das Modell kann dann ohne weitere Bindemittel zusammengesteckt werden. Die Abbildung 9 zeigt einen mäßig gelungenen Prototypen (zu dünnes Papier).

Abb. 9: Prototyp

Websites

Walser, Hans (2013): Würfelecke und Davidstern:

www.walser-h-m.ch/hans/Miniaturen/W/Wuerfelecke/Wuerfelecke.htm

Walser, Hans (2014): Origami im Raum:

www.walser-h-m.ch/hans/Miniaturen/O/Origami_im_Raum/Origami_im_Raum.htm

Walser, Hans (2018): Doppelpyramide im Würfel:

www.walser-h-m.ch/hans/Miniaturen/D/Doppelpyramide_Wuerfel/Doppelpyramide_Wuerfel.htm