Hans Walser, [20090602a]
Ewige PaarlŠufe
1
Worum es geht
Es werden Beispiele
vorgestellt, bei denen durch die Anwendung des Verfahrens von Newton-Raphson
ein ewiger Paarlauf zwischen zwei Werten entstehen.
2
Wurzelfunktionen
2.1
Das einfache Beispiel
Die Funktion 
ist nur fźr 
definiert. Sie
hat die Nullstelle 0.
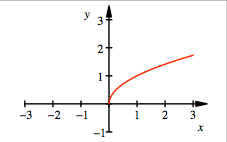
Funktionsgraf
Was geschieht, wenn wir
versuchen, mit dem Verfahren von Newton-Raphson und dem Startwert 
eine Nullstelle
zu bestimmen?
Mit dem MuPAD-Programm
f:=x->sqrt(x):
x[0]:=2:
N:=5:
for n from 0 to N do
x[n+1]:=(x[n]-f(x[n])/f'(x[n])):
end_for:
for n from 0 to N do
print(Unquoted,"
x[".n."]\t= ".x[n]);
end_for:
erhalten wir:
x[0] = 2
x[1] = -2
x[2] = 2
x[3] = -2
x[4] = 2
x[5] = -2
Die Werte pendeln
zwischen 2 und 
. Das ist všlliger Unsinn, denn der Wert 
ist nicht im Definitionsbereich der Funktion und kann daher
nicht weiter verarbeitet werden.
Fźr einen beliebigen
Startwert 
pendeln die
Werte zwischen a und 
.
Beweis:
Damit erhalten wir fźr
die Rekursion nach Newton-Raphson:
Wir sehen, dass die fźr
rein imaginŠre
Zahl 
durch das
Quadrieren wieder reell wird.
2.2
Das subtile Beispiel
Die Funktion 
ist nur fźr 
definiert, das
ist dann auch die Nullstelle.
Was geschieht, wenn wir
wieder versuchen, mit dem Verfahren von Newton-Raphson und dem Startwert 
eine Nullstelle
zu bestimmen?
Wir erhalten erneut:
x[0] = 2
x[1] = -2
x[2] = 2
x[3] = -2
x[4] = 2
x[5] = -2
Beide Werte sind aber
nicht im Definitionsbereich der Funktion.
Fźr einen beliebigen
Startwert 
pendeln die
Werte zwischen a und 
.
Beweis: Fźr 
gilt:
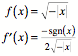
Damit erhalten wir fźr
die Rekursion nach Newton-Raphson:
3
Variation der Vorzeichen
Wir untersuchen die
vier Funktionen:
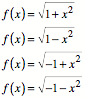
3.1.1
plus plus
Die Funktion 
ist auf ganz 
definiert.
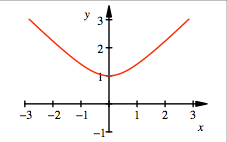
Funktionsgraf
Der Funktionsgraf ist
ein Hyperbelast. Die Funktion hat keine Nullstellen.
Das Verfahren von
Newton-Raphson ergibt mit dem Startwert 
:
x[0] = 2
x[1] = -1/2
x[2] = 2
x[3] = -1/2
x[4] = 2
x[5] = -1/2
Fźr einen beliebigen
Startwert 
pendeln die
Werte zwischen a und 
.
Beweis:
Damit erhalten wir fźr
die Rekursion nach Newton-Raphson:
3.1.2
plus minus
Die Funktion 
ist auf 
definiert.
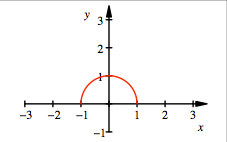
Funktionsgraf
Der Funktionsgraf ist
der obere Halbkreis des Einheitskreises. Die Funktion hat die Nullstellen 
.
Das Verfahren von
Newton-Raphson ergibt mit dem Startwert 
:
x[0] = 2
x[1] = 1/2
x[2] = 2
x[3] = 1/2
x[4] = 2
x[5] = 1/2
Fźr einen beliebigen
Startwert 
pendeln die
Werte zwischen a und 
.
Beweis:
Damit erhalten wir fźr
die Rekursion nach Newton-Raphson:
3.1.3
minus plus
Die Funktion 
ist auf 
definiert.
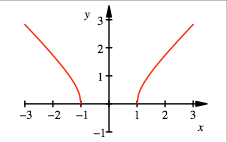
Funktionsgraf
Der Funktionsgraf ist
eine halbe Hyperbel. Die Funktion hat die Nullstellen 
.
Das Verfahren von
Newton-Raphson ergibt mit dem Startwert 
:
x[0] = 2
x[1] = 1/2
x[2] = 2
x[3] = 1/2
x[4] = 2
x[5] = 1/2
Fźr einen beliebigen
Startwert 
pendeln die
Werte zwischen a und 
.
Beweis:
Damit erhalten wir fźr
die Rekursion nach Newton-Raphson:
3.2
minus minus
Die Funktion 
ist fźr reelle
Werte nicht definiert.
Das Verfahren von
Newton-Raphson ergibt aber mit dem Startwert 
:
x[0] = 2
x[1] = -1/2
x[2] = 2
x[3] = -1/2
x[4] = 2
x[5] = -1/2
Fźr einen beliebigen
Startwert 
pendeln die
Werte zwischen a und 
.
Beweis:
Damit erhalten wir fźr
die Rekursion nach Newton-Raphson:
