Hans Walser, [20090517a]
Newton-Raphson in der Ebene
1
Worum es geht
Die Nullstellen einer
Funktion 
kšnnen nach dem
Verfahren von Newton-Raphson bestimmt werden: Wir wŠhlen einen Startwert 
. Dann arbeiten wir mit der Rekursionsformel:
Hoffnung: 
Wir źbertragen nun
dieses Verfahren auf die Situation:
Wir haben also zwei
Funktionen von denselben zwei Variablen. Gesucht sind x und y
so, dass beide Funktionen verschwinden.
2
Schreibweise
Wir verwenden die
folgende Schreibweise:
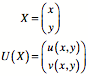
Ferner verwenden wir
die 2,2-Matrix der partiellen Ableitungen:
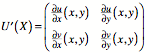
Unter 
verstehen wir
die zu 
inverse Matrix.
3
Das Verfahren von Newton-Raphson
Wir wŠhlen einen
Startwert 
und verwenden
die Rekursionsformel:
Die Formel ist všllig
analog zum eindimensionalen Fall. Sie ist auf beliebige Dimensionen
źbertragbar.
4
Beispiel
Wir arbeiten mit den
Funktionen:
Wir fassen diese
Gleichungen als Abbildungsgleichungen auf. Dabei wird der grźne Kopf in der x,y-Ebene auf den roten Kopf in der u,v-Ebene abgebildet.
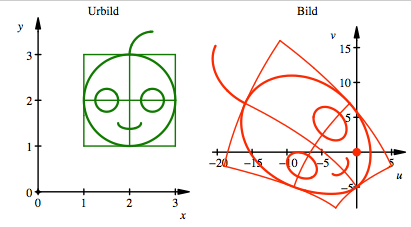
Abbildung
Wir sehen weiter, dass
sich der Nullpunkt im roten Bild auf der linken Backe befindet. Im grźnen
Urbild hat der entsprechende Punkt die geschŠtzten Koordinaten 
. Gesucht sind genauere Koordinaten dieser Nullstelle.
4.1
Startwert (1, 0)
Das Verfahren von
Newton-Raphson liefert mit dem Startwert 
die Tabelle:
|
Schritt n |
x-Wert |
y-Wert |
|
0 |
1 |
0 |
|
1 |
1.5 |
3.666666667 |
|
2 |
1.724261201 |
1.896250397 |
|
3 |
2.399828632 |
1.383561641 |
|
4 |
2.508465442 |
1.465255017 |
|
5 |
2.506191815 |
1.463045114 |
|
6 |
2.506190969 |
1.463043604 |
|
7 |
2.506190969 |
1.463043604 |
Die Nullstelle ist also
. Die Konvergenz ist wie immer bei Newton-Raphson recht
schnell.
In der folgenden Figur
sind zu den Schritten 0 bis 4 die zugehšrigen Punkte 
eingezeichnet.
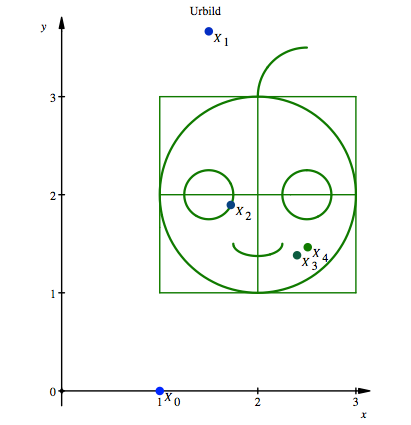
Approximation der
Nullstelle
4.2
Anderer Startwert
Das Verfahren von Newton-Raphson liefert mit dem
geŠnderten Startwert 
die Tabelle:
|
Schritt n |
x-Wert |
y-Wert |
|
0 |
0 |
1 |
|
1 |
3.666666667 |
0 |
|
2 |
2.106060606 |
1.0 |
|
3 |
2.519801608 |
1.544554632 |
|
4 |
2.505014678 |
1.46420491 |
|
5 |
2.506190434 |
1.463043371 |
|
6 |
2.506190969 |
1.463043604 |
|
7 |
2.506190969 |
1.463043604 |
Wir kommen zur selben
Nullstelle.
In der folgenden Figur
sind wieder zu den Schritten 0 bis 4 die zugehšrigen Punkte 
eingezeichnet.
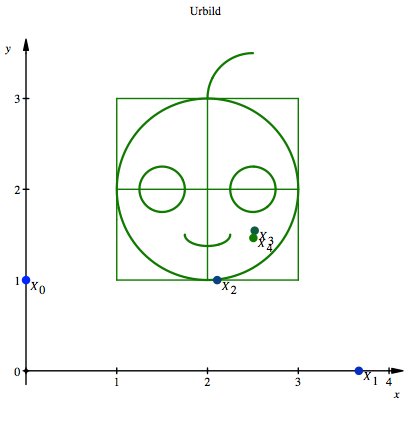
Anderer Weg zur gleichen
Nullstelle
5
Kontrolle
Fźr das
Gleichungssystem
liefert MuPAD:
u:=(x,y)->x^2-2*y^2-2:
v:=(x,y)->3*x*y-11:
glgs:={u(x,y)=0, v(x,y)=0}:
sols:=float(solve(glgs, {x, y})):
print(sols):
die Lšsungen:
{[x = -2.506190969, y = -1.463043604],
[x = 2.506190969, y = 1.463043604],
[x = -2.069056107 I, y = 1.772144629 I],
[x = 2.069056107 I, y = -1.772144629
I]}