Hans Walser, [20110827b], [20150110]
Modell der MinimalflŠche im Oktaeder
Anregung: [Limperg 2011] sowie eine private Mitteilung von G. L., W.
1 Worum geht es?
Wir tauchen ein Kantenmodell eines Oktaeders in eine Seifenlauge ein. Nach dem Herausziehen bilden die SeifenhŠute eine MinimalflŠche mit dem Kantenmodell des Oktaeders als Rand. Diese FlŠche wird als Papiermodell nachgebaut. Dabei zeigt sich ein Link zum DIN-Format.
MinimalflŠche im Oktaeder
2 MinimalflŠche im Oktaeder
Wir beginnen mit einem Kantenmodell des Oktaeders.
Kantenmodell des Oktaeders
Die
folgende Abbildung zeigt die Verzweigungskanten und Verzweigungspunkte im
Innern der MinimalflŠche. An den Verzweigungskanten kommen jeweils drei Ebenen
zusammen, welche wechselseitig Winkel von 
einschlie§en
(Gleichgewichtsbedingung). An den Verzweigungsknoten kommen jeweils vier
Verzweigungskanten zusammen, welche wechselseitig Winkel von 
einschlie§en.
Dieselben Winkel finden wir auch, wenn wir vom Mittelpunkt eines Tetraeders aus
die vier Ecken anpeilen. Dieser Winkel wird beim Modellbau eine zentrale Rolle
spielen.
Verzweigungen
Die MinimalflŠche besteht aus 12 Dreiecken und 6 Vierecken. In der folgenden Abbildung sind sie abwechslungsweise rot, gelb und blau gefŠrbt.
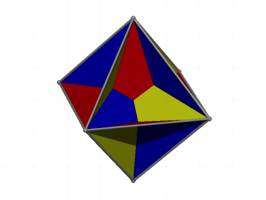
MinimalflŠche
Die folgende Abbildung zeigt lediglich die Dreiecke. Sie bilden vier nach innen gerichtete Pyramiden.
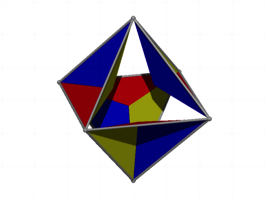
Nach innen gerichtete Pyramiden
Die sechs Vierecke sind Drachenvierecke, deren LŠngsachse auf Oktaederdiagonalen
liegen. Die Ebenen zweier Vierecke mit der LŠngsachse auf derselben
Oktaederdiagonalen sind orthogonal zu einander.
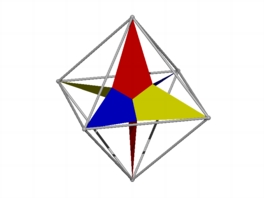
Drachenvierecke
3 Geometrisches Modell
Wir verwenden das Koordinatensystem der folgenden Abbildung.
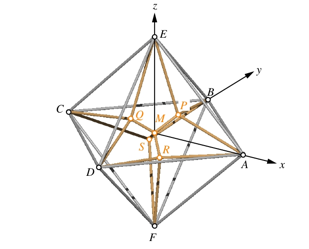
Koordinatensystem
Die Ecken des Oktaeders legen wir wie folgt fest:
FŸr die Verzweigungspunkte ergeben sich folgende sehr einfache Koordinaten:
Die Punkte PQRS sind die Ecken eines Tetraeders.
Aus diesen Koordinaten lassen sich die oben angegebenen Winkel verifizieren.
Zu dieser Lšsung gibt es noch eine zweite Lšsung, welche zur ersten Lšsung punktsymmetrisch ist.
4 Papiermodell
4.1 Modelltyp
Wir stellen ein doppelwandiges Papiermodell mit Einschiebeschlitzen her. Die Dreiecke und Vierecke bestehen also aus zwei Lagen, zwischen welche die Verbindungsfalze eingeschoben werden. Bei der Verwendung von verschiedenen Farben fŸr die Bauteile sind die Verbindungsfalze unsichtbar. Die Verbindungsfalze kšnnen eingeklebt werden; ich habe sie lediglich mit Bostitch-Klammern fixiert.
4.2 Bauteile
Der
stumpfe Schnittwinkel der beiden Diagonalen eines Rechteckes im DIN-Format ist 
, entspricht also dem Winkel, der in unseren Dreiecken und
Vierecken vorkommt. Daher versuchen wir, die Bauteile auf der Basis von Papier
im DIN-Format herzustellen. Ich habe DIN A5 verwendet.
In den folgenden Abbildungen fŸr die Bauteile sind Schnittlinien schwarz, konvexe Faltlinien (ãBergfalteÒ) blau und konkave Faltlinien (ãTalfalteÒ) rot gezeichnet. Konstruktionselemente sind grŸn. Verbindungsfalze etwas dunkler getšnt. Ma§angaben sind VerhŠltnisma§e.
4.2.1 Dreiecke
Aus einem DIN A5 Papier ergibt sich ein Doppeldreieck:
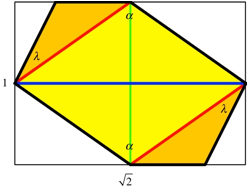
Doppeldreieck
Der
eingezeichnete Winkel 
bei den
Verbindungsfalzen sollte etwa 30¡ messen.
Es sind insgesamt 12 solcher Bauteile erforderlich, also bei Verwendung von drei Farben je vier.
4.2.2 Vierecke
Aus einem DINA5 Papier ergeben sich zwei Vierecke.
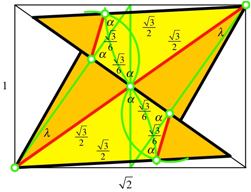
Zwei Drachenvierecke
Wegen der Doppelwandigkeit sind insgesamt zwšlf Vierecke erforderlich, je vier von jeder Farbe.
Die folgende Abbildung zeigt das fertige Modell.
Modell
5 Technisches
Der Zusammenbau der Bauteile ist nicht ganz einfach. Es empfiehlt sich zuerst ein GesellenstŸck.
5.1 Tetraeder
Wir tauchen ein Kantenmodell des Tetraeders in die Seifenlauge. Die entstehende MinimalflŠche hat einen einzigen Verzweigungsknoten, den Mittelpunkt. Die Verbindungen zu den Tetraederecken sind die Verzweigungskanten.
Situation im Tetraeder
Die MinimalflŠche besteht aus sechs Dreiecken, welche dieselbe Form haben wie die Dreiecke bei der MinimalflŠche des Oktaeders.
MinimalflŠche
Die MinimalflŠche besteht aus vier nach innen gerichteten Pyramiden, welche die Spitze gemeinsam haben (Mittelpunkt).
Wir kšnnen daher mit sechs Doppeldreiecken, je zwei in jeder Farbe, die MinimalflŠche des Tetraeders zusammenbauen. Der Zusammenbau ist relativ einfach.
Modell der MinimalflŠche des Tetraeders
5.2 Kollapsmodell
Beim Oktaeder und beim Tetraeder haben wir dieselben vier Pyramiden. Wenn wir also die vier Pyramiden des Oktaeders je um ihre Hšhe gleich orientiert drehen und gleichzeitig den Abstand zum Mittelpunkt reduzieren, kollabiert das Oktaeder zum Tetraeder.
5.3 Ausblick
Gibt es ein Modell, das ohne Leim oder Fixierklammern auskommt?
6 FlŠchenvergleiche
Wir
berechnen den FlŠcheninhalt 
unserer
MinimalflŠche.
FŸr eines der Dreiecke gilt:
FŸr eines der Vierecke gilt:
Aus 
folgt 
. Somit wird:
FŸr die MinimalflŠche erhalten wir:
Wir
vergleichen nun mit der FlŠche, welche sich ergibt, wenn wir die Oktaederkanten
mit dem Mittelpunkt verbinden. Wir haben dann drei sich paarweise orthogonal
durchdringende Quadrate der SeitenlŠnge 
.
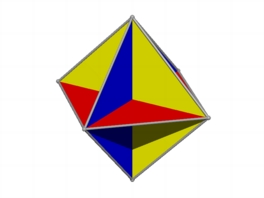
Mittelpunktsebenen
FŸr den FlŠcheninhalt der GesamtflŠche finden wir:
Somit ist:
7 Reduzierte Symmetrie
WŠhrend die MinimalflŠche des Tetraeders die gleiche Symmetriegruppe hat wie das Tetraeder, haben wir bei der MinimalflŠche des Oktaeders nur die Symmetriegruppe des Tetraeders. Wir haben also einen Symmetrieverlust. Das ist allerdings nicht Ÿberraschend, da wir eine Dimension tiefer einen analogen Sachverhalt haben. Der Steinerbaum des regelmŠ§igen Dreiecks hat dieselbe Symmetriegruppe wie das Dreieck.
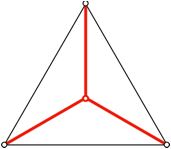
Steinerbaum des Dreieckes
Beim Quadrat sieht die Situation aber anders aus.
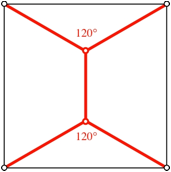
Steinerbaum des Quadrates
Der Steinerbaum des Quadrates hat nur noch die Symmetriegruppe des Rechtecks. Beim Quadrat gibt es noch einen zweiten Steinerbaum, welcher aus dem gezeichneten Steinerbaum durch eine Vierteldrehung entsteht.
Literatur
[Limperg 2011] Limperg, Gerd: SteinerbŠume (auch dreidimensionale) im Experiment. MNU, Der mathematische und naturwissenschaftliche Unterricht. 64/5 (15. 7. 2011) Seiten 284-288.